复杂地形风资源分布计算的研究

徐根发，张伟，刘保松，刘庆超

（1.浙江华电新能源项目筹备处，杭州310017；2.华电电力科学研究院，杭州310030）

输配电技术

复杂地形风资源分布计算的研究

徐根发1，张伟2，刘保松2，刘庆超2

（1.浙江华电新能源项目筹备处，杭州310017；2.华电电力科学研究院，杭州310030）

风资源计算及分布是风电场开发的基础工作，直接关系着微观选址的准确性，影响风电场经济效益。研究了风切变系数与地面粗糙度变化规律、威布尔分布参数随高度变化规律、风资源计算模型等风资源分布的理论，并以某风电场为例进行计算，验证了理论的正确性及实用性，为复杂地形风资源计算及分布研究提供了理论基础及工程应用指导。

复杂地形；风资源；风切变系数；威布尔分布

风电场的规划设计属风电场建设项目的前期工作，需要综合考虑许多方面，包括风能资源的评估、风电场的选址、风电机组机型选择、装机容量确定、风电场的微观选址、风电场并网方式选择、土建和电气设备选择及经济效益分析等。其中，对风能资源的计算和分布研究是风电场开发的基础性工作，直接关系到风电场效益，是风电场建设成功与否的关键因素之一。

本文从风切变系数与地面粗糙度变化规律、威布尔分布参数随高度变化规律及风资源计算模型等方面对风资源计算及分布进行了深入研究，并以某复杂地形的风电场为实例进行验证，说明了理论的正确性及实用性，对准确评估复杂地形风资源具有重要意义。

1 风切变系数与地面粗糙度变化规律分析

1.1 风切变系数的影响因素

风切变系数是风电机组安全设计的重要参数，直接影响到风电场的机组选型。较大的风切变系数将对风电机组叶片根部疲劳载荷产生影响，减小风机寿命，同时还将增大风电机组设计功率损失。

在近地层中，风速随高度的变化显著。造成风在近地层中垂直变化的原因有动力因素和热力因素。前者主要来源于地面的摩擦效应，即地面的粗糙度影响；后者主要表现为与近地层大气垂直稳定度的关系。当大气层结为中性时，湍流将完全依靠动力因素来发展，这时风速随高度的变化服从普朗特经验公式：

式中：Un和ui分别为高度在Zn和Zi处的风速；α为风切变系数。

对于复杂地形，风切变系数不仅受粗糙度影响，还受地形影响。气流通过丘陵或者山地时，受地形影响，在山的向风面下部风速减弱，且有上升气流；在山顶和山的两侧，因为流线加密而风速加强；在山的背风面，因流线辅散，风速将急剧减弱，且有下沉气流。由于重力和惯性力的作用，使山脊的背风面气流形成波动流动。如何对不同地形的风切变系数进行计算分析？本文提出以计算流体力学理论对复杂地形的风资源情况进行模拟，从而推断不同山脉和不同粗糙度下的风切变系数。

1.2 计算流体力学风资源模拟

CFD（计算流体力学）是通过计算机和离散化的数值方法对流体力学问题进行数值模拟和分析的一个新分支。CFD技术可以根据流体力学的规律进行模拟求解，将几何区域分解为小的立方体空间（即网格），并在其中求解复杂的偏微分方程组。流体运动可以通过一组耦合的非线性偏微分方程进行数学描述。

运用质量和动量守恒的平均方程（Navier -Stokes方程）模拟风资源数据，当流体定常且不可压缩时，方程为：

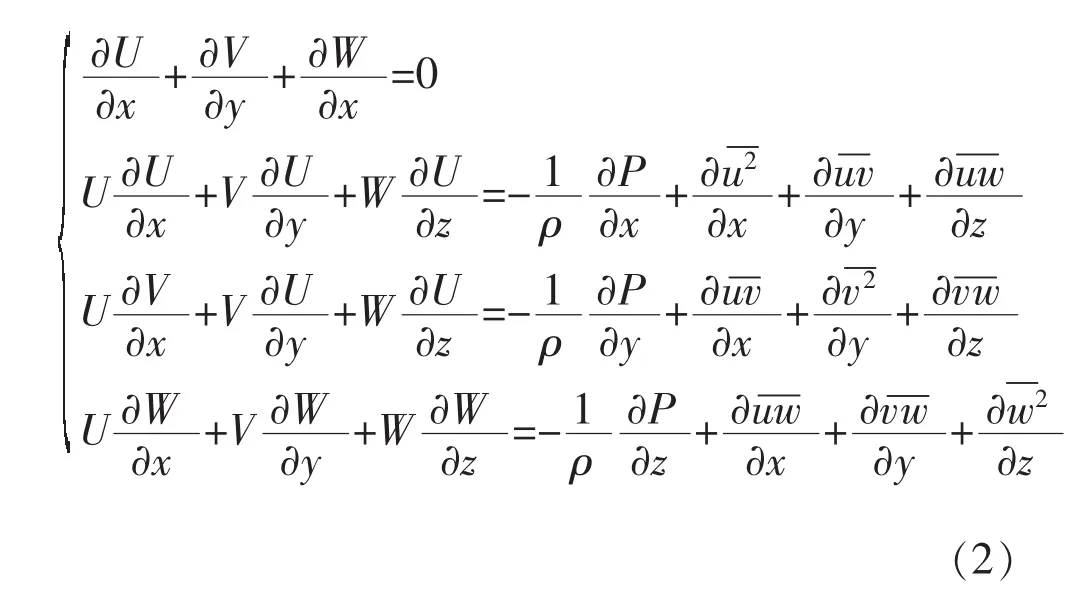
式中：U，V，W是平均风速矢量在笛卡尔空间（x，y，z）中的3个分量；x和y是水平坐标；z是垂直坐标；P为平均压力；ρ为空气密度；u，v，w为湍流波动量。

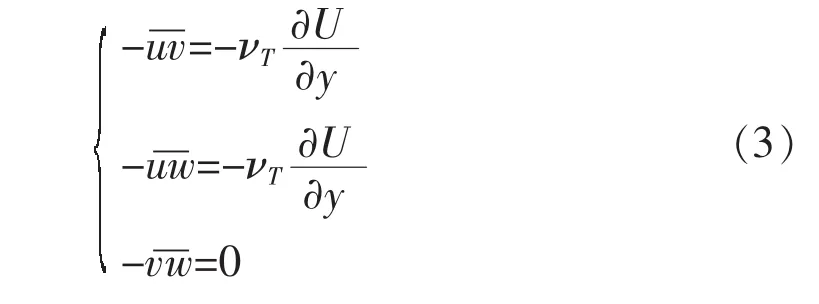
此湍流模型可以求解一个新的输运方程，至此湍流动能即得到分解。

设定边界条件：

（1）入口条件：在表面层计算域入口的垂直平均风速廓线是由艾克曼层通过对数规则给定的。表面层的湍流动能是一个常数，并且随着某个高度依赖值减少到上界条件。

（2）地面条件：地面边界条件在底层网格动量方程中产生一个降低项。利用莫宁-奥布霍夫理论，这一项作为第一层级网格平均风速和真实地表局部粗糙度的一个函数，可以通过对数规则求出。

（3）上界、侧边界以及出口边界条件：在计算域的侧边界应用了一个对称条件，在上界和出口采用均质压力条件。

1.3 主要工况设计

根据复杂地形主要地貌，对地形及地表植被（粗糙度）设定以下边界条件：

（1）山脉共设计2种形式：单独1座山脉和连续的2座山脉。

（2）山脉上粗糙度共设计5级，分别为0.1，0.2，0.3，0.4，0.5。

（3）山脉以外粗糙度设定为0.01。

（4）山脉高度为300 m，倾角共设计5种，分别为20°，30°，40°，50°，60°，70°。

图1为不同地形组合模拟，设风向为180°，即风向全部为南风，因此仅需对南侧坡度进行调整。图1中第一行为单条山脉，每个山脉上建立1个测风测试点，测试10～120 m的风廓线。图1中第二行为连续山脉，分别赋予了不同粗糙度，计算第二排山脉顶部测试点的风廓线，从而可计算出风切变系数与粗糙度的关系，如图2，3所示。

图1 不同地形组合模拟

图2 单条山脉工况风切变分布

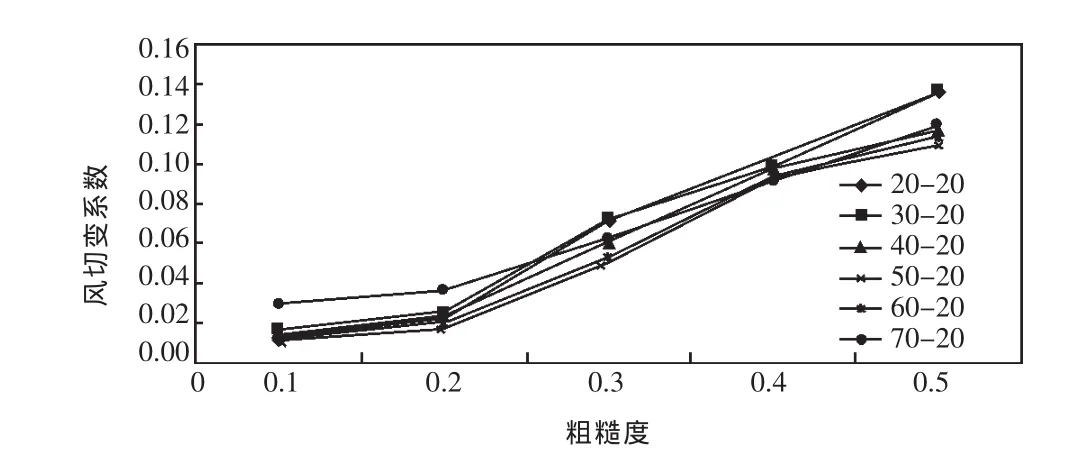
图3 连续山脉风切变分布

本文仅给出了部分角度下的风切变系数，对于非以上角度的山脉，建议采用插值法进行模拟计算，并对不同扇区的风速及倾斜度采用加权方式进行计算。综合风切变系数的计算公式如下：

式中：α为综合风切变系数；ai为山脉倾角为i时的风向频率；αi为山脉倾角为i时的风切变系数。

结合风电场测试点实际测量值，对风切变系数计算的正确性进行验证，对比数据见表1。

表1 主要测风塔风切变系数

从表1对比可知，模拟计算的风切变系数与地形、地貌关系较为吻合，满足要求。

2 威布尔分布参数随高度变化规律分析

在风能利用中，反映风统计特性的一个重要形式是风的频率分布。根据风的频率分布，可推导出评估风电场风能资源的主要标准参数：风功率密度、有效风功率密度等。

用于拟合风速分布的线形很多，通常采用威布尔分布双参数曲线，如式（5）所示：

式中：c，k分别是威布尔分布的尺度参数和形状参数。

根据上式可分别计算各测风塔不同高度的c值与k值，计算结果见表2。

对以上数据进行曲线拟合，可得到各个测风塔c值与k值随高度变化规律：

式中：cn，kn是海拔高度为Hn时的c、k值；ci，ki是海拔高度为Hi米的c、k值；H为海拔高度；H0是测风塔海拔高度。

表2 各个测风塔不同高度的c值与k值

3 风电场区域内风资源分布计算

不同地形下测风塔的代表性半径有所不同。在复杂地形中，测风塔的代表性半径为2 km，据此以各个测风点实测数据，根据不同的地形及地表粗糙度，推算各个风机点的风速分布，主要计算步骤图4所示。

图4 复杂地形风资源计算步骤

运用4号测风塔数据进行检验，模拟风速与实际风速平均误差为4.16%，最小误差为-0.12%，最大误差为25.37%，平均绝对误差为5.83%。通过对比分析，证明模型模拟数据精度较高。

若根据计算流体力学风资源模型所模拟的70 m高度风速，和利用风切变系数计算的60 m高度风速，并与实际风速对比，其平均误差为0.35%，绝对平均误差为0.35%，精度较高，对比见图5。

图5 实测风速、计算流体力学模拟风速及风切变计算风速对比

根据以上分析，运用计算流体力学理论及测风塔70 m高度处风速可对场内任意机位进行同高度风速模拟，再运用风切变理论对其c值和k值进行模拟，更加接近该点实际情况，从而可以估算风场内各点不同高度的风资源分布。

4 结语

复杂地形风资源计算及分布研究对于微观选址具有重要意义。以某风电场为例，总结了适合复杂地形的风切变系数随粗糙度变化规律，同时以某风电场测风塔数据进行了验证，结果误差较小，说明风切变随理论粗糙度变化系数表符合实际情况。利用函数拟合理论，总结出威布尔分布参数随高度变化的规律，并给出计算公式。以计算流体力学理论对复杂地形风资源分布情况进行了模拟，给出了复杂地形风资源评估计算模型，运用该模型进行风资源分析，准确度得到了有效评估。

[1]苏绍禹.风力发电机设计与运行维护[M].北京∶中国电力出版社，1999.

[2]Tony Burton.风能技术[M].北京∶科学出版社，2007.

[3]宋海辉.风力发电技术及工程[M].北京∶中国水利水电出版社，2009.

[4]李正良，孙毅，魏奇科，等.山地平均风加速效应数值模拟[J].工程力学，2010，27（7）32-37.

[5]杨振斌，薛析，桑建国.复杂地形风能资源评估研究初探[J].太阳能学报，2004，25（6）∶744-749.

[6]张友飞，黄鹤楼，沈祥家，等.慈溪北部沿海风能资源的计算及分析[J].浙江气象，2007（29）∶22-25.

[7]GB/T 18710-2002风电场风能资源评估[S].北京：中国标准出版社，2003.

[8]Yuan Chun-hong，Xue Heng，Yang Zhenbin.A Numerical Modeling Study for Offshore Windspeed[J].Acta Energiae Solaris Siniea，2004，25（6）∶740-743.

Research on for Wind Resources Calculation and Distribution in Complex Terrain

XU Gen-fa1，ZHANG Wei2，LIU Bao-song2，LIU Qing-chao2
（1.Zhejiang Huadian New Energy Project Preparatory Office，Hangzhou 310017，China；2.Huadian Electric Power Research Institute，Hangzhou 310030，China）

Wind resources calculation and distribution are the basis work of the wind farm development, which are directly related to the accuracy of the micro site and influence economic benefit of wind farm.This paper studies the theory for the wind resource distribution such as the change rule of the wind shear coefficient and ground roughness，change of weibull distribution parameters by height variation and wind resource calculation model.Furthermore，by taking the wind farm as a case to calculate,it verifies the correctness and practicability of the theory，providing theoretical basis and guidance of engineering applications for the study of resources distribution in complex terrain.

complex terrain；wind resources；wind shear coefficient；weibull distribution

TM615

：B

：1007-1881（2013）07-0001-04

2013-04-22

徐根发（1964-），男，浙江兰溪人，高级工程师，硕士，从事水电及新能源发电技术研究。

（本文编辑：龚皓）

浙江省重大科技项目-复杂地形风电场开发关键技术研究及示范（2009C11022）。