基于最小二乘法及BP神经网络的盾构故障预测
2013-06-18陈国忠邢东杰
陈国忠,邢东杰
CHEN Guo-zhong,XING Dong-jie
(广东华隧建设股份有限公司,广东 广州 510635)
机械故障的预测是机械故障诊断技术的重要组成部分,通过预测可以保障机械设备长期安全、稳定、满负荷运行。参数跟踪法是目前机械故障预测中经常采用的方法,该方法首先保存机械运行时特征参数的历史数据,并利用其预测机械的发展趋势,来了解机械的未来运行情况。盾构是一个复杂的系统,在其运行过程中经常会出现一些复杂多变的情况,在预测可能出现的问题时采用单一的模型不能全面客观的预测出系统的运行状况,因此,需要选用其他的预测模型来反映机器的运行,采用最小二乘拟合法是一种较理想的优化方案,这种方法能利用提供的信息计算出一条直线,或者曲线,使得线上的数据与原始数据间的距离平方和达到最小。该曲线可以较好的表达出时间序列变化的走势,但是如果出现时间序列变化平缓,以及完全非线性的系统,则不能很好解决。同时,神经网络由于具有学习功能,且能很好地解决非线性系统的问题,这样,可以弥补最小二乘法的不足,将这二者结合起来,可以充分利用二者的优点,对盾构未来运行状态进行预测,同时,将其与单一的BP 神经网络的预测结果进行比较。
1 故障预测常用方法种类及特点
常用的故障检测方法有曲线拟合、时间序列模型、卡尔曼滤波、灰色预测、人工神经网络。
1)曲线拟合法 本方法简单实用,好理解,较多地应用在监控机械装置的系统,缺点是预测误差结果比较大[1]。
2)卡尔曼滤波法 计算量小、预测精度高,主要用于线性系统,在非线性系统中需要进行扩展,但其模型的不确定性很差。
3)灰色预测 该方法需将两个部分进行置换,即“随机过程”转换为“灰色过程”,把“随机量”处理成“灰色量”,然后在理论系统的模型GM(1,1)中进行处理[2]。
4)神经网络 具有学习记忆功能,能很好解决非线性系统问题,不对预测模型做限制,同时还能把的历史数据完整映射到未来的数据库中,可广泛用在故障检测中。实际使用广泛的神经网络预测有:BP神经网络和自组织特征映射网络[3]。
2 最小二乘法与BP神经网络相结合的预测方法
采用最小二乘法与BP 神经网络相结合的方法来预测故障需要对所选取的数据样本集进行直线最小二乘法的拟合,然后用BP 神经网络算法进行计算,最后将这些值作为样本集,输入到BP神经网络模型来进行训练预测。
2.1 样本数据的选取
盾构掘进过程中,PU 电流表现的是非平稳且复合的一种随机过程。在本文模型中,选择PDV系统中的一些历史数据来预测其电流值的波动变化情况。数据时间范围是PDV 数据库中2012年10月4日到5日两天的据运行记录,并且以1h为时间间隔提取100 个PU 电流数据样本作为样本集进行训练。
2.2 BP神经网络模型的构建
在构建神经网络之前,需将数据进行归一化处理,将归一化的数据样本构建成BP 神经网络模型。在本论文的神经网络模型中,训练函数,学习函数,传读函数,性能函数,训练次数,训练误差,学习率分别为:traingdx,learngdm,logsig,mse,1000 次,0.0001,0.08. 输 入 层,输出层及隐层分别为:6,1,5。
2.3 最小二乘法的直线拟合过程
根据最小二乘法的理论[4]及BP 神经网络的模型可知,要预测故障,既是对出现故障的时间序列的预测,而预测时间序列X={Xt!t=0,1,2…m},实际上就是利用已知的{xk,xk-1…xk-n+1}来求xk+1。预测时间序列的最小二乘法拟合过程如下:
首先令
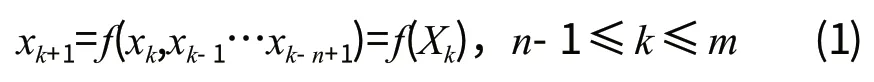
在(1)式中,Xk=(xk,xk-1…xk-n+1)T。由于f(Xk)具有相当的复杂性,因此可将式中的f(Xk)分为两部分:线性部分和非线性部分,可表示为如下的形式:
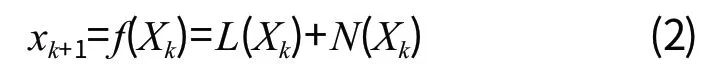
(2)式中的L(Xk)和N(Xk)可表示为如下形式:
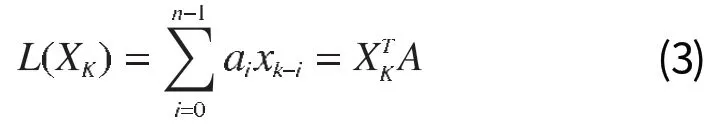
其中 A=(a0,a1…an-1)T
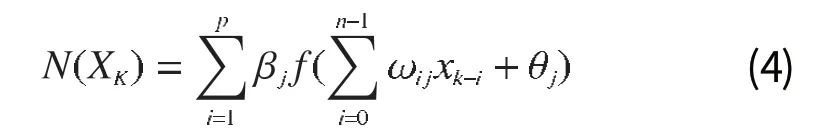
上式中,β为隐层神经元的数目。可知(2)式中的参数可由两部分求取,第一部分用最小二乘法计算L(Xk)中的参数ai,第二部分用最小二乘法的残差计算N(Xk)中的βj,ωij,θj。
用最小二乘法求出L(Xk)中的参数ai,由上式(3)有

在(7)式中,E=(em,em-1,…en)T∈Rm-n,Y=(xm,xm-1,…xn)T∈RM-N,
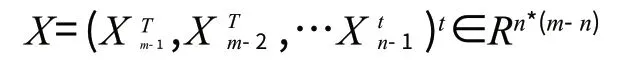
根据最小二乘法,可以计算出参数A满足

求出A以后将其代入公式(5)中可以得到下式:
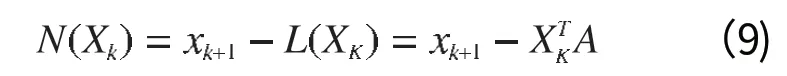
根据(9)式计算能得到最小二乘法拟合后的BP 神经网络的输入和输出样本

将上述拟合结果得到的数据样本再通过BP神经网络的算法对样本计算,得到其对应的各个参变量值,即给出Xk,得到期望值N(Xk),其中k=n-1,n…m,然后把这些值作为样本集,用在BP 神经网络中来训练整个网络。
3 盾构PU电流序列预测应用
3.1 单一的BP神经网络的预测结果
单一的BP神经网络采用以1h为间隔所提取得100个PU电流数据作为样本集对进行训练,采用输入连续的6个PU电流值,紧接着输出相连续的一个PU电流值,即输入与输出层节点数比例为6∶1,隐层节点数为5,将网络进行收敛,当达到预定精度以后,预测其结果如图1中曲线所示。

图1 单一的BP神经网络的盾构PU电流时间序列预测
3.2 最小二乘法及BP神经网络相结合的预测结果
用上面的样本集数据,对最小二乘法与BP神经网络合成样本进行训练,并进行网络收敛,当达到预定精度,预测结果如图2 中曲线所示。

图2 基于合成的BP神经网络的盾构PU电流时间序列预测
3.3 两者结果比较
图1和图2 中的两条预测线分别代表PU 实际电流变化曲线(实线)以及用神经网络预测的电流变化曲线(虚线)。可以看到,在图2 中,这两种曲线的变化趋势比较接近,仅有极少的时间序列点有较大偏差,而图1 中的两条曲线则在多个时间序列段出现较大的偏差,两条曲线走势明显偏离,所以,可以认为采用合成的BP 神经网络算法预测到的PU 电流时间序列精度较高,比采用单一的BP 神经网络更能客观反映盾构的实际电流变化情况。虽然有个边点出现误差,也是未考虑机组负荷的影响。因此,整体上说合成的BP 神经网络算法对盾构的PU 电流还是具有很高的预测能力。
4 总 结
上述内容主要采用最小二乘法与BP 神经网络结合的方法对盾构的故障进行预测,将二者结合起来,可以充分利用二者的优点,优势互补。笔者将其应用到了实际的工作中,起到了良好的预测效果。
[1]蒋 瑜,杨 雪,阮启明.机械设备故障规律及运行趋势预测方法综述[J].机电一体化,2001,(03):14-17.
[2]陈敏泽,周东华.动态系统的故障预报技术[J].控制理论与应用,2003,20(06):820-822.
[3]苏春华,罗 雷,海 军,等.基于BP 神经网络的汽车发动机寿命预测[J].军事交通学院学报,2009,11(04):50-51.
[4]王惠文,吴载斌,孟 洁,等.偏最小二乘回归的线性与非线性方法[M].北京:国防工业出版社,2006.
