CuFeSb电子结构和磁性的第一性原理研究
2013-06-17于海林江学范谷全超
潘 妍 ,于海林 ,b,钱 斌 ,b,江学范 ,b,郭 磊 ,吕 群 ,谷全超
(a.常熟理工学院 物理与电子工程学院;b.江苏省新型功能材料重点建设实验室,江苏 常熟 215500)
自从发现铁磷族化合物和铁硫族化合物的超导电性和反铁磁序有关以来[1-8],人们认为超导配对机制与自旋涨落密切相关[9-13],超导电性和自旋涨落有关在超导态的自旋共振方面得到了进一步的证实[11-15]. 为了阐明自旋涨落在超导配对机制上的本质作用,在未掺杂的母体化合物的磁性,以及这类材料的磁性和超导电性相互作用方面做了许多研究工作.虽然铁磷族化合物和铁硫族化合物有相似的层状结构和费米面的拓扑性,它们未掺杂母体化合物的反铁磁序(AFM)是完全不同的.例如,LaOFeAs[16]和BaFe2As2[17]表现出“单条纹”(single-stripe)反铁磁序,而铁硫族元素化合物中的Fe1+yTe[18]显示出“双条纹”(double-stripe)形状的反铁磁序.
这两类材料在反铁磁序结构上的显著差别,引发了关于磁性起源方面的大量争论.对于铁磷族化合物超导配对机制的解释并不适用于Fe1+yTe.有趣的是除了费米面驱动的磁性机制外,多种基于局域磁矩超交换相互作用的模型也相继被提出来[19-24].最近,考虑局域磁矩和巡游电子耦合的模型也被提了出来[19,22,25-26].此外,Yin等提出了一个统一的微观模型来解释各种反铁磁关联现象[27].该模型认为局域磁矩和巡游电子共存,局域自旋的反铁磁超交换耦合与双交换铁磁相互作用竞争,“single-stripe”和“double-stripe”反铁磁序都可以用阴离子距Fe平面的高度来解释.
近来,Moon和Choi利用第一性原理计算,发现阴离子高度对这类材料基态磁结构有重要影响[28].他们的工作显示如果阴离子Te的高度ZTe小于临界值(~1.71 Å),Fe1+yTe的反铁磁序将从“single-stripe”向“dou⁃ble-stripe”转变,这和实验结果完全一致.同时还发现,从总能的角度看,随着Zanion的增加,有向铁磁态转变的趋势.最近,钱斌等在实验上首次合成了具有与铁磷族化合物类似结构的新型铁磷族化合物CuFeSb[29],并发现其具有完全不同于目前研究中的铁磷族化合物和铁硫族化合物的金属性反铁磁序,而是表现出金属性铁磁序.然而,目前为止,还没有针对CuFeSb的磁性和电子特性的理论研究.本文采用第一性原理对CuFeSb的磁性和电子特性进行计算,阐明其金属性铁磁特性产生的物理机制.
1 计算方法
密度泛函(DFT)下的广义梯度近似(GGA)是目前较为准确的电子结构计算的理论方法[30-31],它是电子密度及其梯度的泛函[31],并把密度分布的空间变化包括在其中,实现了可较大幅度减少局域密度近似(LDA)误差的目的[32].离子和电子间的相互作用采用投影缀加平面波(projector augmented wave,PAW)[33]方法来处理.这种方法可以相当程度地减少过渡金属或第一行元素的原子所必需的平面波的数量,并且对于磁性化合物而言,PAW方法要优于超软赝势方法.本文采用的计算软件为Vienna ab-initio Simulation package(VASP),截断能选取500 eV,K点采样选择Monkhorst-Pack方法.对铁磁相的计算,采用的是CuFeSb的四方单包,其K点采样使用8×8×5,而对反铁磁相的计算采用的2×2×1的超包,其K点采样使用4×4×5.
2 结果与讨论
2.1 结构特性
CuFeSb的四方结构属于P4/nmm空间群,如图1(a)所示.在对原子结构进行弛豫优化时,我们选择的晶格常数为实验值a=3.934 Å,c=6.251 Å[29],在本工作中,我们只对原子的内部坐标进行了弛豫,计算结果如表1所示.从表1中我们发现计算结果和实验值[29]能够很好地吻合.弛豫以后的Sb原子距Fe原子的距离为1.839 Å,远远高于Moon和Choi提出的临界值[28].这是CuFeSb表现出铁磁序的一个原因,这一点和Moon等通过计算得出的趋势是一致的.
2.2 磁性和电子特性
对于CuFeSb的磁性和电子特性的计算,其铁磁相采用的是如图1(a)所示的四方相单包.而对反铁磁序的计算,采用的2×2×1的超包,其Fe原子平面磁矩的排列,我们考虑了三种构型,即C型、E型和G型,如图1(b)-(d)所示. 我们对弛豫以后的总能量进行比较发现,铁磁相具有最低的总能,即CuFeSb的基态磁结构为铁磁相.对其磁性的计算我们得到其四方相单包的磁矩为 4.50 μB,这和前期的实验结果[29]能够很好地吻合.
我们对CuFeSb的能带和态密度进行了详细计算,如图2和图3所示.从图2中我们可以看出CuFeSb表现出典型的金属性,这和实验结果完全一致.自旋向上的能带结构和自旋向下的能带结构总体上相近,如图2(右)和(左)所示.其主要差别在于在-4 eV~0.0 eV范围内,自旋向下的能带和自旋向上的能带相比,其色散性更明显,这一点主要由Fe原子d轨道上不同自旋方向的电子的占据情况决定.如图3所示,相比于Cu原子,Fe原子的3d轨道其局域性减小,巡游性增强.其自旋向下的电子态主要由反键轨道占据,这样导致其自旋向下的能带较自旋向上的能带有更大的色散性.从Fe的平面内轨道dx2和dxy来看,其自旋向下的电子态基本上完全由反键轨道占据,这表明平面内Fe原子间的相互作用是比较强的.考虑到Sb原子距Fe原子平面的高度较大,导致Fe原子和Sb原子间的相互作用减弱,从而相应导致平面内Fe原子的相互作用增强.

图1 (a)CuFeSb四方相单包结构示意图,黑色表示Fe原子,深灰色表示铜原子,灰色表示Sb原子.(b)、(c)、(d)分别表示Fe原子平面原子磁矩的排列,白色和黑色分别表示磁极化方向相反的两类Fe原子.(b)表示C型(collinear),(c)表示E型(bicollinear),(d)表示G型(checkerboard)
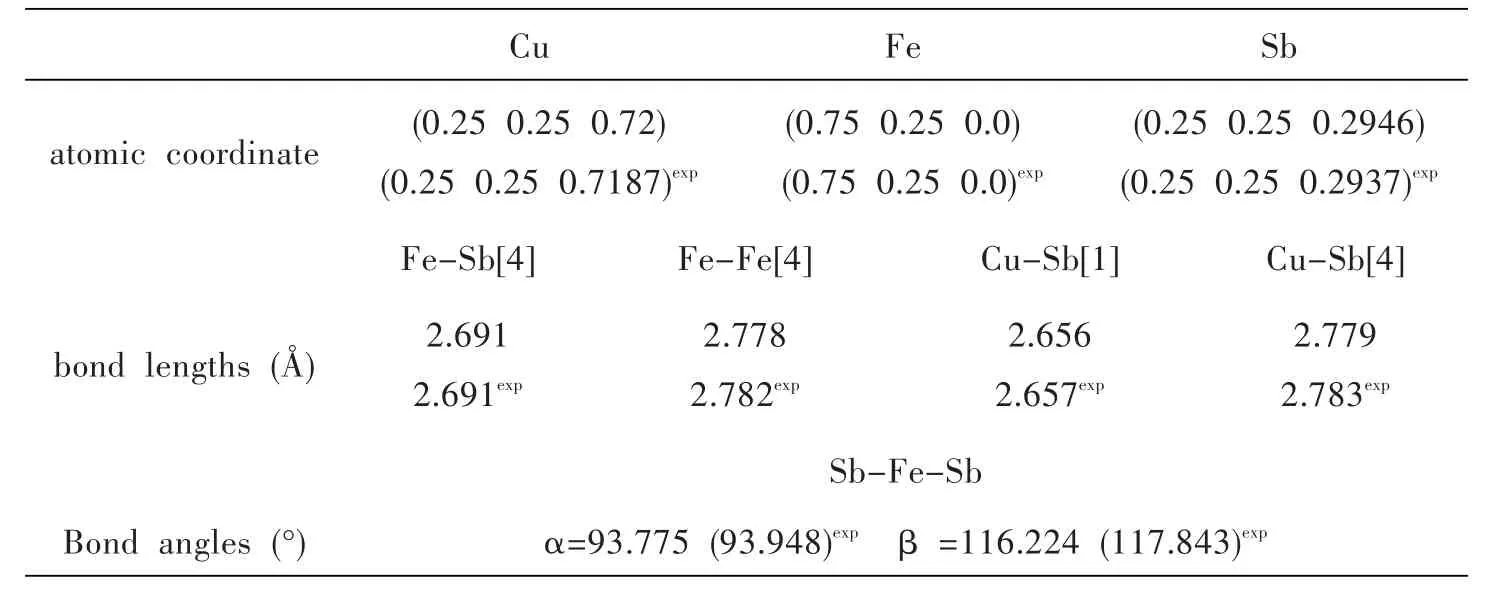
表1 弛豫以后的CuFeSbC的结构参数
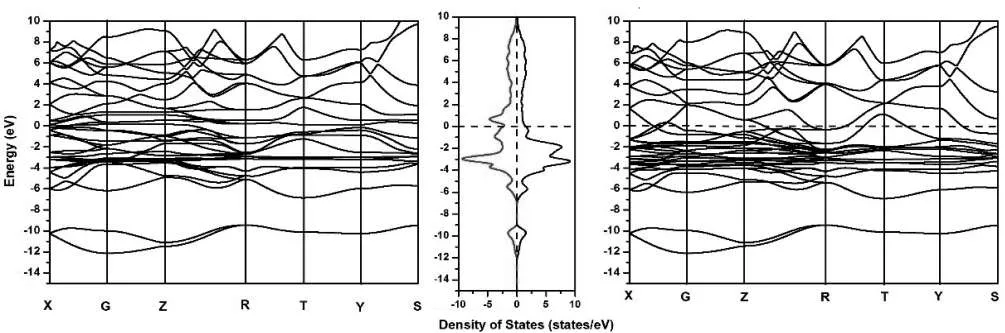
图2 铁磁相CuFeSb的能带和相应的态密度.(左)自旋向下的能带,(中)态密度图,红色曲线表示自旋向下的态密度,黑色曲线表示自旋向上的态密度,(右)自旋向上的能带
3 总结
利用第一性原理计算对CuFeSb的晶体结构、磁性和电子特性进行了研究.从能带和态密度的计算结果来看,CuFeSb表现出典型的金属性,这一点和实验结果完全一致.通过对Fe原子的d轨道进行深入分析,发现其d轨道的局域性相对减弱,巡游性增强,并发现其平面内Fe原子的相互作用较强,其金属性铁磁序与平面内Fe原子的相互作用增强有关.
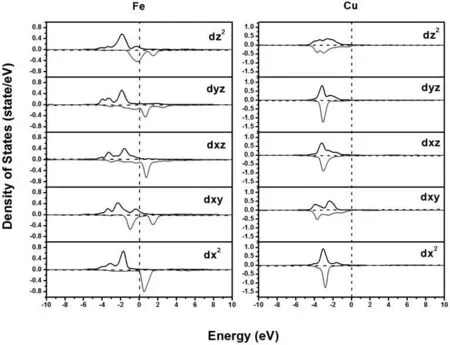
图3 Fe(左)和Cu(右)原子的d轨道态密度图
[1]Zhao J,Huang Q,Cruz C de la,et al.Structural and magnetic phase diagram of CeFeAsO1-xFxand its relation to high-temperature superconductivity[J].Nat Mater,2008,7:953.
[2]Luetkens H,Klauss H H,Kraken M,et al.The electronic phase diagram of the LaO1-xFxFeAs superconductor[J].Nat Mater,2009,8:305.
[3]Drew A J,Niedermayer C,Baker P J,et al.Coexistence of static magnetism and superconductivity in SmFeAsO1-xFx as revealed by muon spin rotation[J].Nat Mater,2009,8:310.
[4]Chen H,Ren Y,Qiu Y,et al.Coexistence of the spin-density wave and superconductivity in Ba1−xKxFe2As2[J].Europhys Lett,2009,85:17006.
[5]Chu J H,Analytis J G,Kucharczyk C,et al.Determination of the phase diagram of the electron-doped superconductor Ba(Fe1−xCox)2As[J].Phys Rev B,2009,79:014506.
[6]Nandi S,Kim M G,Kreyssig A,et al.Anomalous Suppression of the Orthorhombic Lattice Distortion in Superconducting Ba(Fe1-xCox)2As2Single Crystals[J].Phys Rev Lett,2010,104:057006.
[7]Liu T J,Hu J,Qian B,et al.From(π,0)magnetic order to superconductivity with(π,π)magnetic resonance in Fe1.02Te1−xSex[J].Nat Mater,2010,9:718.
[8]Katayama N,Ji S,Louca D,et al.Investigation of the Spin-Glass Regime between the Antiferromagnetic and Superconducting Phases in Fe1+ySexTe1-x[J].J Phys Soc Jpn,2010,79:113702.
[9]Ahilan K,Ning F L,Imai T,et al.19F NMR investigation of the iron pnictide superconductor LaFeAsO0.89F0.11[J].Phys Rev B,2008,78:100501.
[10]Nakai Y,Ishida K,Kamihara Y,et al.Evolution from Itinerant Antiferromagnet to Unconventional Superconductor with Fluorine Doping in LaFeAs(O1-xFx)Revealed by 75As and 139La Nuclear Magnetic Resonance[J].J Phys Soc Jpn,2008,77:073701.
[11]Christianson A D,Goremychkin E A,Osborn R,et al.Unconventional superconductivity in Ba0.6K0.4Fe2As2from inelastic neutron scattering[J].Nature,2008,456:930.
[12]Lumsden M D,Christianson A D,Parshall D,et al.Two-dimensional resonant magnetic excitation in BaFe1.84Co0.16As2[J].Phys Rev Lett,2009,102:107005.
[13]Chi S,Schneidewind A,Zhao J,et al.Inelastic Neutron-Scattering Measurements of a Three-Dimensional Spin Resonance in the FeAs-Based BaFe1.9Ni0.1As2Superconductor[J].Phys Rev Lett,2009,102:107006.
[14]Mook H A,Lumsden M D,Christianson A D,et al.Neutron scattering patterns show Superconductivity in FeTe0.5Se0.5likely results from itinerant electron fluctuations[J].e-print arXiv,2009,0904:2178.
[15]Qiu Y,Bao W,Zhao Y,et al.Spin Gap and Resonance at the Nesting Wave Vector in Superconducting FeSe0.4Te0.6[J].Phys Rev Lett,2009,103:067008.
[16]Cruz C de la,Huang Q,Lynn J W,et al.Magnetic order close to superconductivity in the iron-based layered LaO1-xFxFeAs systems[J].Nature,2008,453:899.
[17]Huang Q,Qiu Y,Bao W,et al.Neutron-Diffraction Measurements of Magnetic Order and a Structural Transition in the Parent BaFe2As2Compound of FeAs-Based High-Temperature Superconductor[J].Phys Rev Lett,2008,101:257003.
[18]Bao W,Qiu Y,Huang Q,et al.Tunable(δπ,δπ)-Type Antiferromagnetic Order in α-Fe(Te,Se)Superconductors[J].Phys Rev Lett,2009,102:247001.
[19]Ma F,Lu Z-Y,Xiang T.Arsenic-bridged antiferromagnetic superexchange interactions in LaFeAsO[J].Phys Rev B,2008,78:224517.
[20]Si Q,Abrahams E.Strong Correlations and Magnetic Frustration in the High Tc Iron Pnictides[J].Phys Rev Lett,2008,101:076401.
[21]Yildirim T.Origin of the 150-K Anomaly in LaFeAsO:Competing Antiferromagnetic Interactions,Frustration,and a Structural Phase Transition[J].Phys Rev Lett,2008,101:057010.
[22]Ma F,Ji W,Hu J,et al.First-Principles Calculations of the Electronic Structure of Tetragonal α-FeTe and α-FeSe Crystals:Evi-dence for a Bicollinear Antiferromagnetic Order[J].Phys Rev Lett,2009,102:177003.
[23]Hu J,Xu B,Liu W,et al.Unified minimum effective model of magnetic properties of iron-based superconductors[J].Phys Rev B,2012,85:144403.
[24]Hu J,Ding H.Local antiferromagnetic exchange and collaborative Fermi surface as key ingredients of high temperature superconductors[J].e-print arXiv,2011,1107:1334.
[25]Wu J,Phillips P,Castro Neto A H C.Theory of the Magnetic Moment in Iron Pnictides[J].Phys Rev Lett,2008,101:126401.
[26]Johannes M D,Mazin I I.Microscopic origin of magnetism and magnetic interactions in ferropnictides[J].Phys Rev B,2009,79:220510.
[27]Yin W-G,Lee C-C,Ku W.Unified Picture for Magnetic Correlations in Iron-Based Superconductors[J].Phys Rev Lett,2010,105:107004.
[28]Moon C-Y,Choi H J.Chalcogen-Height Dependent Magnetic Interactions and Magnetic Order Switching in FeSexTe1-x[J].Phys Rev Lett,2010,104:057003.
[29]Qian B,Lee J,Hu J,et al.Ferromagnetism in CuFeSb:Evidence of competing magnetic interactions in iron-based superconductors[J].Phys Rev B,2012,85:144427.
[30]Marlo M.Density-functional study of bulk and surface properties of titanium nitride using different exchange-correlation functionals[J].Phys Rev B,2000,62:2899.
[31]李震宇,贺伟,杨金龙.密度泛函理论及其数值方法新进展[J].化学进展,2005,17(2):192-202.
[32]黄美纯.密度泛函理论的若干进展[J].物理学进展,2000,20(3):199-219.
[33]Blöchl P E.Projector augmented-wave method[J].Phys Rev B,1994,50:17953.
