复合材料层压板低速冲击损伤的有限元模拟

杨 鹏，刘海涵

（西北工业大学航天学院，陕西 西安 710072）

0 引言

复合材料层压板在使用中受到外来物体低速冲击后容易在内部产生严重的分层损伤，已有大量的国内外学者［1－6］对复合材料层压板损伤模式开展了研究，取得了不少的研究成果。层间分层的存在，将造成复合材料结构的强度和刚度显著下降，限制了复材的应用。因此，探究复合材料层压板在低速冲击载荷作用下的损伤模式一直是复合材料领域内的研究重点。

1 试验部分

复合材料层压板低速冲击试验数据由北京航空材料研究院提供。试验件材料体系为U3160／6421。铺层方式为［45°／0°／－45°／90°］4S，单层厚度 0.16 mm，分别进行了4种能量的冲击试验，冲击能量分别为10J，15J，20J，23J。复合材料层压板分层损伤投影面积的大小与冲击能量关系如图1所示。

图1 冲击能量与损伤面积的关系

2 有限元模拟

基于ABAQUS软件平台，建立复合材料层压板动力学分析模型，利用用户自定义子程序VUMAT对ABAQUS进行二次开发，编写复合材料单向板的本构关系及损伤起始判据与损伤扩展准则。层间界面层利用有厚度的cohesive单元来模拟，根据试件的结构和载荷形式确定有限元分析的模型和边界条件，并选用合理的材料失效准则及接触类型，通过改变冲击锤的初速度来模拟不同冲击能量下的层压板损伤情况，并获取冲头的冲击力时间历程曲线等数据。

2.1 复合材料损伤模式

复压材料结构在面外低速冲击载荷作用下的损伤形式主要包括纤维断裂、基体失效及分层损伤等。已有很多学者对其损伤性能进行了研究，取得许多研究成果，其中包括Tsai失效准则［7］和Hashin失效准则［8－9］等。模型中使用的单层板失效准则包括纤维断裂、纤维挤压、基体开裂和基体挤裂4种基于应力的失效形式。

纤维断裂的表达式为:

纤维挤压的表达式为:

基体开裂的表达式为:

基体挤裂的表达式为:

XT，XC为单向板在纤维方向上的拉伸、压缩强度；YT，YC为单向板垂直纤维方向上的拉伸、压缩强度；S12为层压板面内剪切强度。冲击过程中，损伤区域的材料性能将退化，使用单元删除的方法来模拟材料性能的退化。根据不同的损伤模式，选择的单元删除方案如下:当某一单元同时满足纤维断裂和基体开裂时，将此单元删除；当某一单元同时满足纤维挤压和基体挤裂时，将此单元删除。

利用ABAQUS中提供的界面单元来模拟复合材料层间界面。同时，研究选用二次名义应力判据来判断损伤起始，层间损伤的扩展采用混压模式的能量准则。

2.2 有限元模型及边界条件

模型尺寸为150mm×100mm×5.12mm，每个单层均建立一层实体单元，单层厚度为0.14 mm，每2层实体单元插入1层0.02mm的3D界面单元，共计32层实体单元和31层界面单元，层压板的铺层形式见试验部分。复合材料单层板的材料性能参数为:E11＝120GPa，E22＝E33＝9.87GPa，ν12＝ν13＝0.307，ν23＝0.48，G12＝G13＝4.46GPa，G23＝3.33GPa，XT＝1693 MPa，XC＝942MPa，YT＝32.8MPa，YC＝198MPa，S12＝S13＝S23＝94.1 MPa。层压板的界面断裂韧性参数为:GIC＝215J／m2，GIIC＝GIIIC＝510J／m2。层压板试验件的底部支撑是一个180mm×108mm×5mm刚体，中间开有125mm×75mm的矩形通孔。冲头为直径16 mm的半球体（设置为刚体），设定冲锤质量与试验中冲头的质量相同，模型中接触类型定义为通用接触。完整的冲击分析模型如图2所示。

边界条件及载荷:

a.给定冲头一个大小与其重量相等、方向沿冲击方向的集中力来模拟试验时的重力作用。

b.限制冲头除Z向平动之外的所有自由度。

c.给定冲头初速度。

d.提取层压板上ABCD节点建立一个SET，限制其3个方向的移动，用来模拟试验中的四点螺栓固支的边界条件。

e.限制底部支撑刚体的所有自由度。

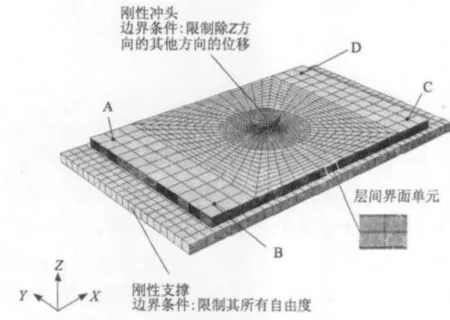
图2 层压板冲击模型

3 有限元结果及分析

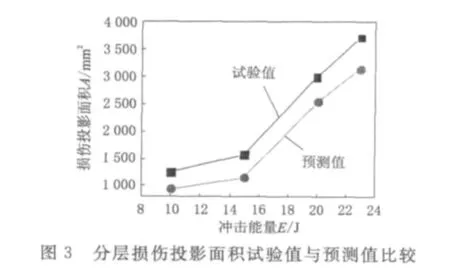
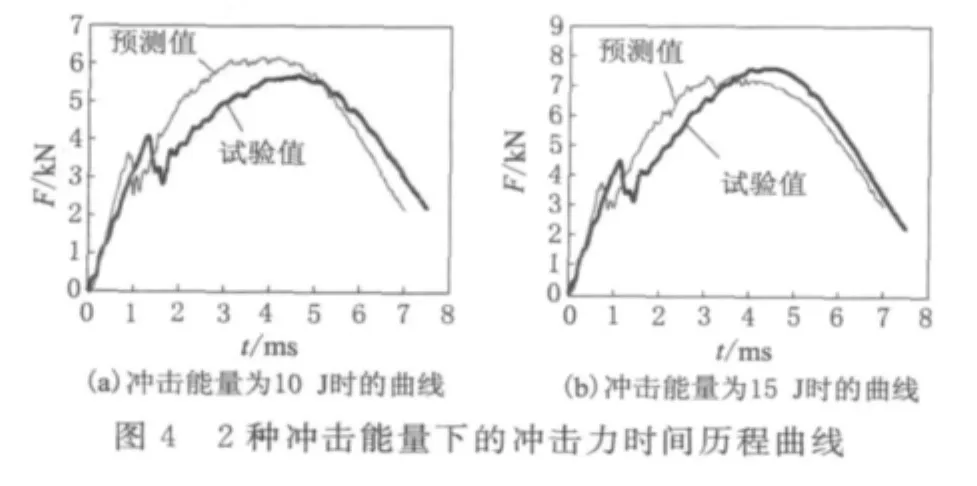
有限元分别模拟了试验中的4种能量的冲击过程。有限元模拟得到的不同能量下的分层投影面积大小与试验值对比如图3所示。有限元模拟得到的分层损伤投影面积与试验值吻合较好。2种冲击能量（10J，15J）下的冲锤的冲击力时间历程曲线如图4所示。从图4中可以看出，有限元模拟可以很好地预测最大冲击力以及低速冲击过程中冲击力的变化情况。在冲击能量为10J和15J情况下，冲击力均在1.5ms左右时出现明显的载荷下降，这时层压板内的损伤主要是基体开裂和大范围的分层。

4 结束语

通过ABAQUS建立的复合材料层压板低速冲击载荷作用下的有限元模型，模拟不同冲击能量下层压板的损伤过程。将有限元模拟得到的冲锤冲击力时间历程曲线及损伤面积和已有的试验数据对比，取得了很好的一致性，验证了模型的准确性和合理性。

［1］Hou J P，Petrinic N，Ruiz C，et al.Prediction of impact damage in composite plates［J］.Composite Science and Technology，2000，60（2）:273－281.

［2］Olsson R.Analytical prediction of large mass impact damage in composite laminates［J］.Composites，2001，32（9）:1207－1215.

［3］Turon A，Camanho P P，Costa J，et al.A damage model for the simulation of delamination in advanced composites under variable－mode loading［J］.Mechanics of Materials，2006，38（11）:1072－1089.

［4］朱炜垚，许希武.复合材料层合板低速冲击损伤的有限元模拟［J］.复合材料学报，2010，27（16）:200－207.

［5］沈 真，杨胜春，陈普会.复合材料层压板抗冲击行为及表征方法的实验研究［J］.复合材料学报，2008，25（5）:125－133.

［6］Pinho S T，Robinson P，Lannucci L.Fracture toughness of the tensile and compressive fibre failure modes in laminated composites［J］.Composites Science and Technology，2006，66（13）:2069－2079.

［7］Tsais W.A survey of macroscopic failure criteria for composites materials［J］.Reinforced Plastics ＆ Composites，1984，3（1）:40－62.

［8］Hashin Z，Rotem A.A fatigue failure criterion for fiber reinforced materials［J］.Journal of Composite Materials，1973，7（4）:448－464.

［9］Hashin Z.Failure criteria for unidirectional fiber composites［J］.Journal of Applied Mechanics，1980，47（6）:329－334.