基于聚类算法的虚拟单元布局研究

王 琴，冯定忠，范佳静，鲁洪祥

(浙江工业大学机械工程学院，浙江 杭州 310032)

随着市场经济全球化的加剧，每个制造业企业都面临着变幻莫测的全球化市场竞争的压力，然而现在的制造系统一般都不具备可重构性，因此需要发展一种能够通过系统快速重构来适应动态多变产品需求的新型制造系统——可重构制造系统(Reconfigurable Manufacturing System，RMS)。但是，当生产系统快速做出重大改变时，重构单元布局却需要花费大量的时间和费用，为解决这一难题，Mclean C.R.等人于 1982 年［1］提出了虚拟单元(Virtual Manufacturing Cell，VMC)，它强调根据生产任务变化快速重构制造系统资源。

有资料表明，在制造业中，总经营费用的20%～50%是物料搬运费用，而优良的布局设计可使这一费用减少10% ～30%［2］。布局问题本身是经典的组合优化问题，具有NP特性，因此可重构制造系统的虚拟单元布局问题成为了现代制造业的难题之一。

目前，已有不少学者对虚拟单元进行了研究，例如，Irani等［3］提出了两阶段法来形成虚拟制造单元;Kannan［4］在过程布局中提出了很多以零件族为导向的计划规则，他们显示了虚拟制造单元的完美性;Ko和Egbelu［5］对VMCS设计提出了一个方法论;Sarker等［6］开发出基于工艺路线和调度而不是单元共享的VMC生成方法;Saadettin［7］等提出了如何进行VMCS布置的模型，通过将模型线性化后采用GA进行求解。

本文希望以设备放置时与它所有相邻的设备关联度和最大为目标，其实质上也就是相当于以物流最小为目标，采用遗传算法求解虚拟单元布局问题，然后对虚拟单元布局进行优化。

1 虚拟单元布局问题建模与求解

1.1 设备相似系数

假设可重构制造系统以一个零件－机器关系矩阵(part－machine incidence matrix)的二元矩阵来表示(如图 1 所示)，其中 (P1，P2，…，Pk，…，Pn)表示零部件，(M1，M2，…，Mi，…，Mm)表示机器，如果第Pk种零部件由第Mi种机器进行加工，则矩阵的元素(Pk，Mi)为1;否则为0。

图1 零件机器二元矩阵

本文研究所提出的相似系数是根据Mcauley在1972年提出的Jaccard相似系数演变而得到的。Jaccard相似系数是利用零件－机器的0－1矩阵，根据其相似性来制定零件与零件或机器与机器之间的相似系数。机器i和机器j 之间的相似系数为Sij，其计算公式如下:

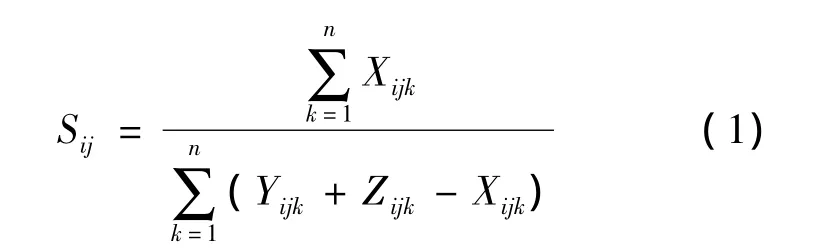
式中:k表示零件，k=1，2，…，n，n 为零件的总数量;i，j表示机器序号，i=1，2，…，m，j=1，2，…，m，m为机器的总数量;Xijk表示若零件k共同访问机器i和机器j，那么为1，反之为0;Yijk在零件k访问机器i不访问机器j时为1，反之，零件k访问机器j不访问机器i时为0;Zijk在零件k访问机器j不访问机器i时为1，反之，零件k访问机器i不访问机器j时为0。

可以通过式(2)计算出各机器间的相似系数矩阵。

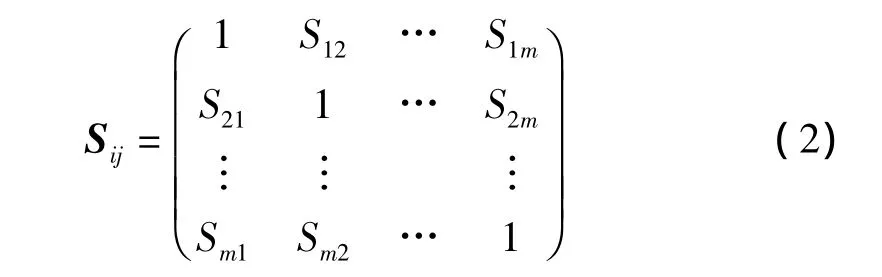
1.2 虚拟单元布局问题的建模

首先，给出如下简化与假设(如图2所示):(1)设备形状都抽象为矩形;(2)设备布局类型为直线多行型布局，这个布局有P行、Q列。假设现在一共有m台设备，虚拟单元布局问题建模描述如下:

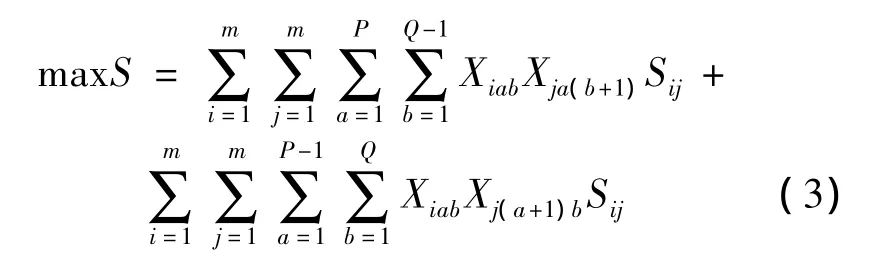
式中:a表示布局的某行，a=1，2，…，P，P 为布局的总行数;b表示布局的某列b=1，2，…Q，Q为布局的总列数;S为总的相似系数值目标函数;Xiab表示第i个设备位于第a行第b列;Sij为设备i和设备j的相似系数。

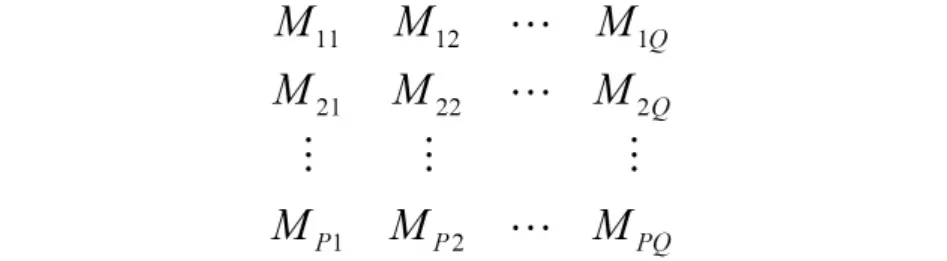
图2 P行Q列的直线多行型布局

考虑设备位置唯一性的约束，给出了如式(4)所示的约束条件。

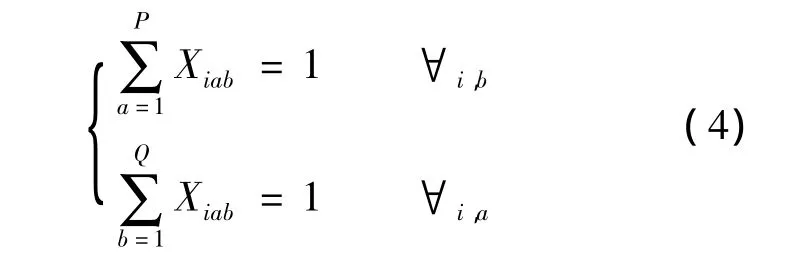
2 虚拟单元布局问题的求解

定义I={i/i=1，2，…，m}为m台机器构成的集合，定义J={j/j=1，2，…，m}为这些机器所组成的一种序列。

2.1 编码

对于一般的多行布局，机器排序采用直接编码的方式，但是需要进行改进。因为这是一个P行Q列的多行布局，那么就有P×Q个位置，而现有机器为m台，即会产生P×Q－m=k个空余位置。(m1，m2，…，mj，…，mm，…，mm+k)为布置在(1，2，…，j，…，m，…，m+k)位置上的机器所构成的序列，其中假设空余位置也放着机器，但令此机器在此位置上所构成的序列用0来表示，其中，该编码中隐含着约束关系为P×Q－m=k。假设有一个4行4列的布局，有14台机器要放入其中，如图3所示。

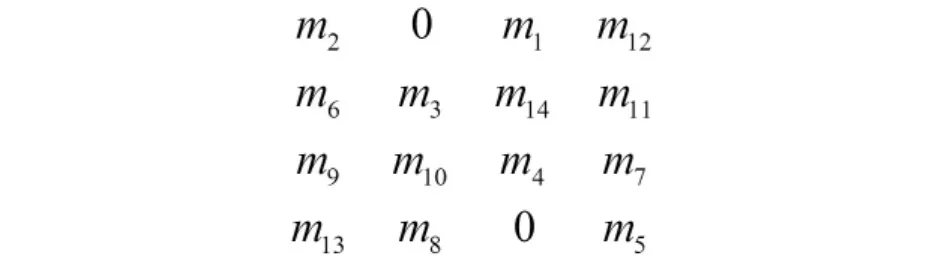
图3 4行4列的直线多行型布局(1)

(2，0，1，12，6，3，14，11，9，10，4，7，13，8，0，5)就是这个4行4列布局中机器的染色体完整编码。

2.2 适应度函数

遗传算法在搜索进化过程中一般不需要其他外部信息，仅用评估函数值来评估个体或解的优劣，并作为以后遗传操作的数据，评估函数值又称作适应(fitness)。适应度值是遗传算法中描述个体性能的主要指标，染色体个体的适应度值越高，则表明该个体越优秀;反之，适应度值越低，则表示个体越容易被淘汰。由于目标函数为最大问题，根据遗传算法的特点，其具体适应度函数就是前面提到的目标函数，得到数学表达式如下:

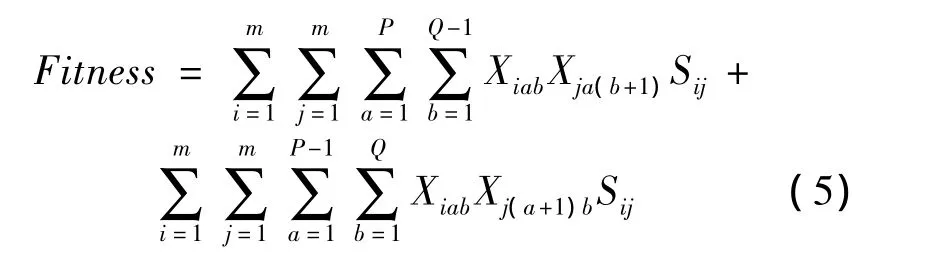
2.3 选择

本文采用精英保留策略与轮盘赌相结合的方法，个体适应度值由大到小排列，选取群体中10%的优秀个体保留至下一代，该部分优秀个体不参与交叉变异，剩余90%的子代采用轮盘赌选择进入下一代。轮盘赌的选择机制，即个体被选中的概率与其适应度大小乘正比，设种群大小为n，个体i的适应度为 Fi，则个体 i被选中的概率为 Pi=，即适应度高的个体被选中的概率大。

2.4 交叉

本文对机器编码序列采用PMX(部分匹配交叉)策略对染色体进行交叉，即先分别随机产生2个交叉点，交换2个父串之间的区域，然后对交叉点以外的区域按交叉点内的匹配关系逐一替换，这里需要改进的是若匹配区域中有0这个编码，则应该舍弃，重新随机产生2个交叉点，以此循环往复。

图4所示为另外一个4行4列的直线多行型布局，其完整染色体编码分别为(1，5，7，8，0，2，6，12，10，13，3，0，9，11，14，4)。

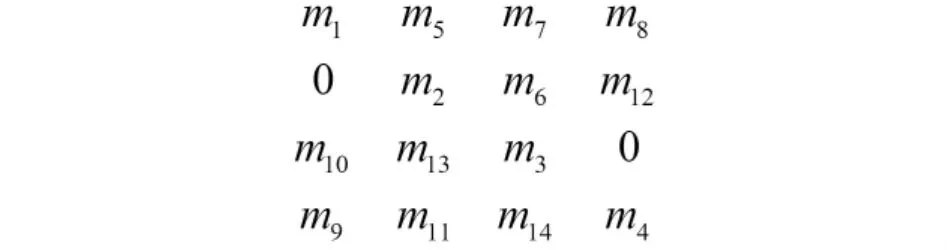
图4 4行4列的直线多行型布局(2)

图3和图4的2个染色体的PMX操作如图5所示。

2.5 变异

对于设备编码序列，就是在机器序列编码染色体的1～m+k位之间随机选择2个数，相互交换。

2.6 评价调整

在每一次迭代完成时，为了提高群体进化水平，本算法还加入了评价调整系统，也就是每次迭代完成后的父代群体和子代群体合并，并按照适应度的高低进行排列，选择适应度高的N个群体作为下一次迭代的父代群体，以此保证每次迭代完成后的群体均为最优群体，并采用最优群体作为后代复制的基础。

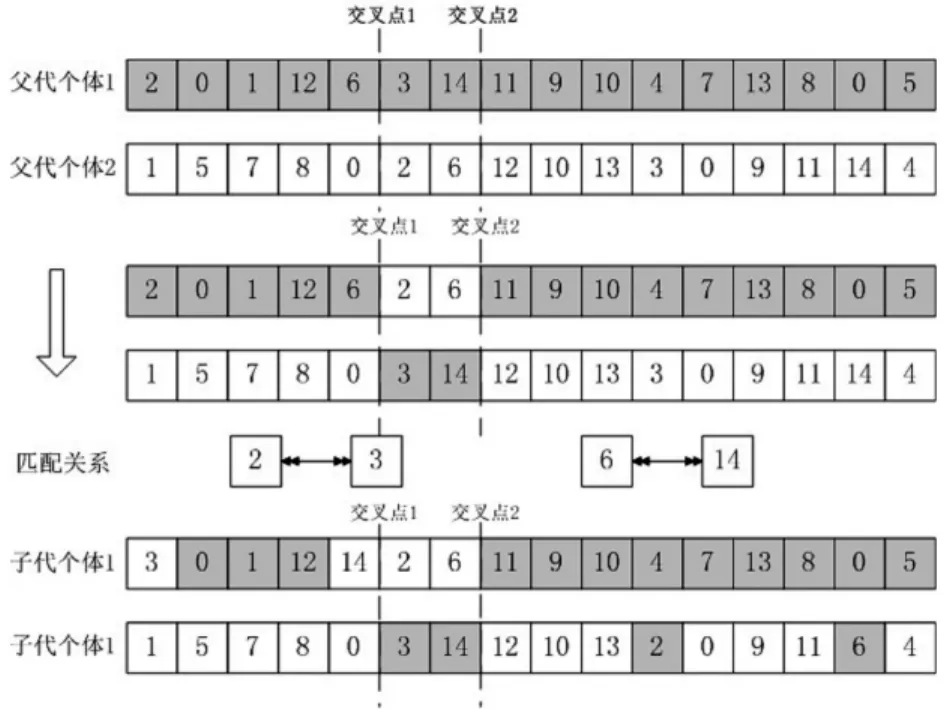
图5 PMX操作示意图

2.7 终止条件

迭代次数达到规定的最大值为终止条件。

3 算例

考虑一个10台机器的虚拟单元布局问题，设备布局参数见表1。

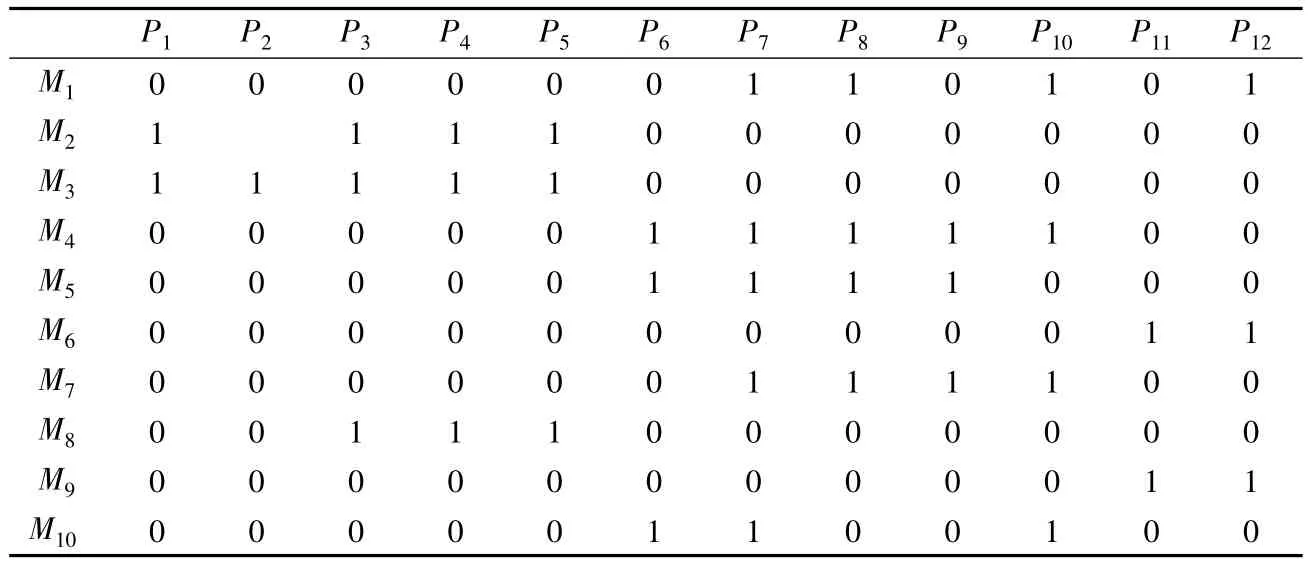
表1 设备布局参数

首先根据聚类算法得到10个设备之间的相似度值分别为

根据大量的试验，可以确定遗传操作参数取值如下:12个零件在10台设备上进行加工，分3行4列进行布局，迭代的最大代数为1000代，交叉概率为 pc=0.2，变异概率为 pm=0.01，精英群体所占比例为0.1，采用前面所述的遗传算法求解上述车间设备虚拟单元布局优化问题，优化结果如图6和图7所示，其中图6和图7的横坐标都表示迭代代数，图6的纵坐标表示最优个体的适应度值，图7的纵坐标表示整体的适应度值。

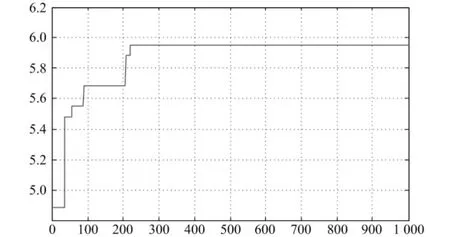
图6 最优个体适应度变化

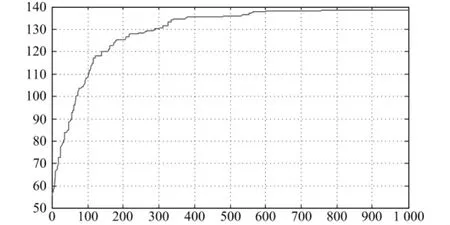
图7 整体适应度变化

由图6可知，最优个体适应度为5.9500。

求得的最优设备布局如下:

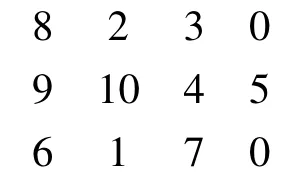
结果分析:(1)最好解出现在219代。(2)219代之后，每代中的最优适应度趋于稳定。整体适应度值有小的波动，表明没有超级个体出现，种群保持了良好的多样性。

4 结束语

本文对虚拟单元布局进行了研究，通过一个数值算例，运用改进的遗传算法，使目标函数更好更快地收敛于最优解，得出了一个最优解的单元布局。此单元布局可以更好地实现可重构制造系统，使制造系统既保持高的生产率，又有高的柔性和设备利用率。此外，人力资源对单元布局是个十分重要的因素，在进一步的研究中，可以将人力资源这块融入到单元布局中去。人的因素包括了很多方面，如团队效应、人员的工资成本及人员分配等，因此进一步考虑人的因素对单元布局问题的求解是十分必要的。

［1］ McLean CR，Bloom HM，Hopp TH.The virtual manufacturing cell［C］//Proceedings of the 4th IFAC/IFIP conference on information control problems in manufacturing technology.Gaithersburg，MD:Massachusetts Institute of Technology Press，1982:1 －9.

［2］ 李志华，曾海红，陈立平，等.多单元制造系统布局设计［J］.工程设计学报，2007，14(3):194－198.

［3］ Irani SA，Cavalier TM，Cohen PH.Virtual manufacturing cells:exploiting layout design and intercell flows for the machine sharing problem［J］.International Journal of Production Research，1993，31(4):791－810.

［4］ Kannan VR.Analysing the trade－ off between efficiency and flexibility in cellular manufacturing systems［J］.Production Planning and Control，1998，9(6):572 －579.

［5］ Ko K－C，Egbelu PC.Performance comparison of static and dynamic cellular manufacturing system ［J］.Proceedings of the First Group Technology/Cellular Manufacturing World Symposium，2000(4):1－6.

［6］ SARKER B R，L I Z.Job routing and operations scheduling:a network － based virtual cell formation approach［J］.Journal of the Operational Research Society，2001，52(3):673－681.

［7］ Saadettin ErhanKesen，SanchoyK Das，Zulal Gungor.A genetic algorithm based heuristic for scheduling of virtual manufacturing cells(VMCs)［J］.Computer and Operations Research，2010，37(6):1148－1156.