地空测控链路OFDM信道估计

孙志刚，张 晶

(中国电子科技集团公司第五十四研究所，河北石家庄050081)

0 引言

地空测控链路用于完成对无人飞行器的遥控、遥测、跟踪定位和载荷信息传输，为保证测控任务可靠性，一般包括窄带上行、下行链路和宽带下行链路。窄带链路完成遥控、遥测和测距功能，采用扩频抗多径、抗干扰传输体制，具有较高的通信可靠度。随着载荷数据速率的提高和应用环境的复杂，又由于无人飞行器大动态运动特点，地空测控链路具有较大的多普勒频移和快速变化的多径衰落，宽带下行链路需具有较强的抗大多普勒、抗多径平衰落和频率选择性衰落的能力。OFDM是近年来移动通信和无线网络广泛采用的抗多径衰落宽带通信技术［1］，其可适用的运动速度一般为120 km/h，要适应地空测控链路信道大动态特点，还需要提高OFDM对快速变化信道的信道估计能力，并控制传输开销。本文提出利用地空测控窄带链路的信道估计辅助宽带链路进行信道估计的方法。

1 OFDM信道估计系统基带模型

对于OFDM系统中的相干检测，信道估计就是对从发送天线到接收天线之间的无线信道频率响应进行估计，从而得到所有子载波的参考相位和幅度值，以达到对信源数据的正确解调［2］。OFDM系统相干检测的系统框图如图1所示。

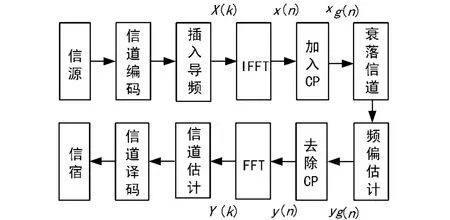
图1 OFDM系统基带框图

发送信号在带有加性白高斯噪声(AWGN)的多径衰落信道中传输，假设接收端已完成正确的定时和频偏估计，并进行了补偿，则接收信号yg(n)可以表示为:

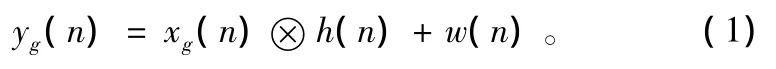
式中，h(n)为信道的时域冲激响应;w(n)为加性白高斯噪声。

对于地空测控链路，认为信道是准静止的，即在一个OFDM符号内信道是近似不变的。这样，信道模型可表示为:

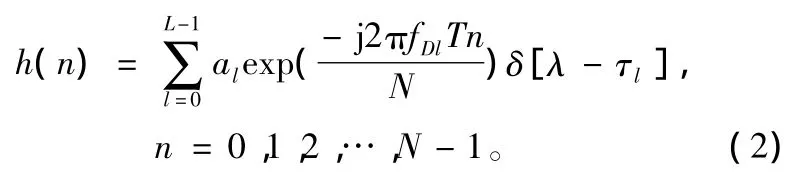
式中，L为多径的总路径数;al为第l径的幅度，fDl为第l径的多普勒频移;τl为第l径的时延;N为子载波数;T为OFDM符号有效长度;λ为离散化时延参数。

去掉循环前缀后，经FFT变换，接收信号的频域表达式为:

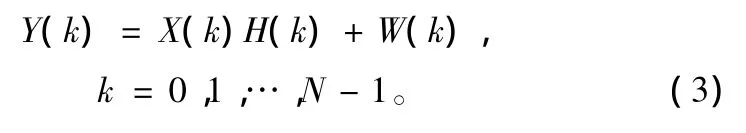
式中，X(k)、Y(k)、H(k)和W(k)分别对应于x(n)、y(n)、h(n)和w(n)的傅里叶变换;若不考虑fDl的存在，即子载波间保持正交性，则有

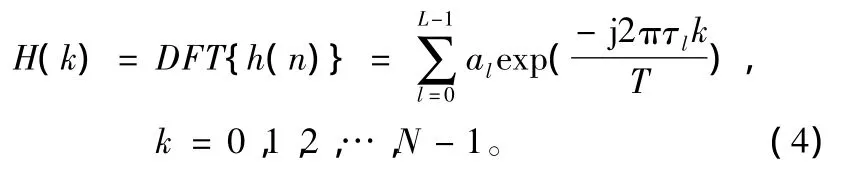
因此，就OFDM系统而言，信道估计就是要估计出每个子载波上的频率响应H(k)。

2 信道估计算法

地空测控窄带上行、下行链路采用直接序列扩频BPSK调制发射和隐分集瑞克接收技术，具有测距、多普勒测量和多径及延时估计等功能，由于窄带链路与宽带链路信道在频段和时间、空间上一致，其多径分布基本一致，因此窄带链路信道估计可用于辅助宽带链路进行信道估计。宽带链路信道主要多径数L及其对应延时τl与窄带链路信道估计参数基本一致，窄带链路信道估计的多普勒频偏通过频率比例换算可得到宽带链路各子载波多普勒频偏粗估计fDl0，再利用OFDM导频序列完成各子载波多径幅度al估计和多普勒频偏fDl的精确估计。

导频插入图案如图2所示［3］，灰色的框即为导频符号插入处，更多子载波通过频域方向的复制而得到。在包含N个子载波的OFDM系统中，以2个OFDM符号为一组，频域每隔Nf1或Nf2(Nf1＜Nf2)个子载波交错插入一个导频符号。

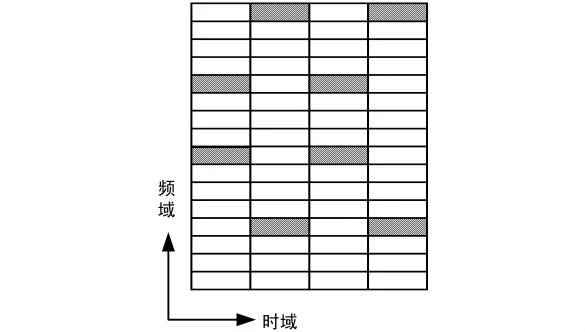
图2 导频插入图案

对于第m个OFDM符号，其完整的频域信号的表示式为:

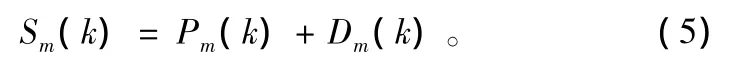
式中，Pm(k)为频域导频符号;Dm(k)为频域数据符号;在接收端，信号经过时变多径的无线信道，假设时间和频率同步已经完成，则DFT输出端的接收信号可表示为:

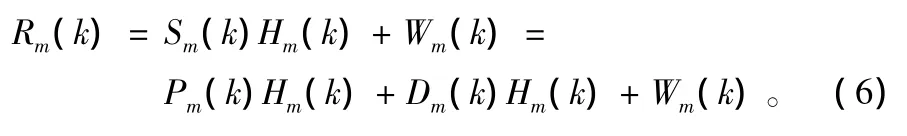
式中，Hm(k)即为在第m个OFDM符号的第k个子载波上的信道频率响应;Wm(k)为高斯噪声在第m个OFDM符号的第k个子载波上的频率响应。

利用LS(Least Squares)算法，对每个OFDM符号中插入的导频符号位置的信道特性进行估计，得到导频符号处的信道估计为:

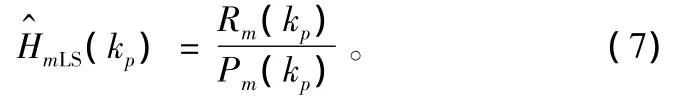
3 仿真及分析

对于上述设计的信道估计算法进行仿真验证，仿真参数如下:子载波数为N=1 024，循环前缀Ng=256，采样率为12 MHz;QPSK调制。导频符号插入方式如下:

① 对于文献［4］和文献［5］，一个OFDM 符号的1 024个子载波中均匀插入256个导频符号，即每隔4个子载波插入一个导频符号;

②对于本算法，按照图2的插入方式，1 024个子载波中，单数OFDM 符号依次间隔4、12、4、12、…个子载波插入导频符号;双数OFDM符号依次间隔12、4、12、4、…个子载波插入导频符号，即一个OFDM符号中包含128个导频符号。

信道采用4径的多径传输信道模型，每径的功率谱为Jakes模型，其中主径的多普勒频率分别设为fd=10 Hz和fd=15 kHz，其他3个副径的功率衰落分别为 －10 dB、－20 dB和 －25 dB，时延分别为2.5 us、5 us和10 us。

图3是主径多普勒频率fd=10 Hz时，3种算法的误码率性能比较。可以看出，在多普勒频率较小时，文献［5］算法与本文设计的算法性能相近，而文献［4］算法的性能略有下降。这是因为，文献［5］算法与本文算法均是先利用导频子载波的LS信道估计值，完成对其他所有子载波的线性插值后，再进行基于DFT的时域滤波;文献［4］则是在对导频子载波完成LS信道估计后直接进行时域滤波，前两者不存在用于IDFT变换的有效样点数小于多径信道最大延迟时间的问题，而且更多的样点数使前者比后者具有更好的性能。

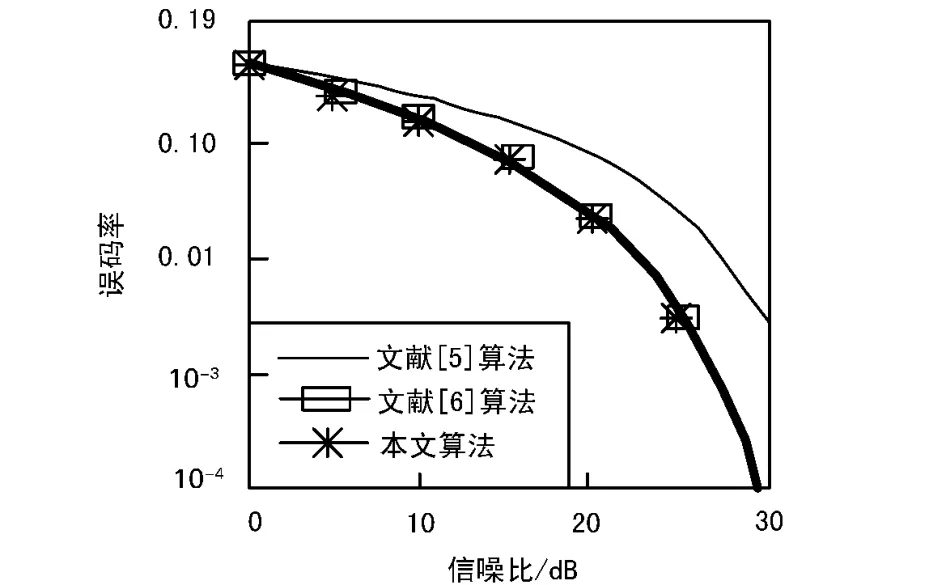
图3 fd=10 Hz时3种算法的误码率性能比较

图4是主径多普勒频率fd=15 kHz时，3种算法的误码率性能比较。可以看出，当主径多普勒频率很大，以至于超出文献［4］和文献［5］中算法的估计能力时，这2种算法的性能明显变差，即使在信噪比较大的情况下也不能使性能有所改善;也就是说，多普勒频率的增大，使信道的时变性加快，插入的导频符号已不能适应信道快速变化的要求，由此估计出的信道特性也已远远偏离实际信道的特性，从而造成大量的误码，而且这种性能已与信噪比没有太大的关系，只与信道估计的误差有关。本文设计的算法，由于可以依据系统提供的相关参数，预先计算最大的多普勒频率，以及确定具有大多普勒频率路径的信道特性，并加以消除，从而使其待估部分的信道已呈现缓慢的时变特性，此时算法中设计的导频符号可以正确反映和跟踪该部分的信道变化情况，因此最后得到的总的信道估计值与实际的信道特性基本一致，从图4中亦可以看到多普勒频率的增大，对系统的误码率性能不会产生太大的影响。

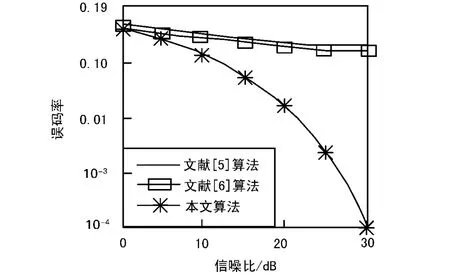
图4 fd=15 kHz时3种算法的误码率性能比较

4 结束语

针对地空测控链路的应用环境和特点，对基于OFDM技术的信道估计问题展开了研究。首先建立了用于信道估计的系统基带模型，然后为地空测控链路设计了特有的导频插入方式和信道估计算法，并在多径传输信道下，将新算法与文献［4］、文献［5］中的算法进行了仿真验证和比较，结果证明新算法更能适应快速时变信道的使用要求，且具有良好的信道估计性能。

［1］尹长川，罗 涛，乐光新.多载波宽带无线通信技术［M］.北京:北京邮电大学出版社，2004.

［2］刘解华，杨东凯，常 青，等.航空移动通信中OFDM信道估计方法的研究［J］.航空学报，2007，28(2):380－384.

［3］HAN H M，HO W C.Channel Estimation for OFDM Systems Based on Comb-type Pilot Arrangement in Frequency Selective Fading Channel［J］.IEEE Trans on Consumer-Electronics，1998，44(1):217 －225.

［4］ZHOU Zhi-gang，CHENG Shi-xin，CHEN Ming，et al.An Improved Channel Estimator with Real-time ISI Free Window Tracking for OFDM Systems［C］∥IEEE 15th International Symposium on PIM-RC 2004，2004:2 416 －2 420.

［5］赵知劲，尹 霆.基于前向平均和时域滤波的OFDM信道估计算法［J］.计算机仿真，2007，24(9):120－123.