一种针对RSA抗侧信道攻击的改进窗口算法

赵跃华，赵 加，韩 牟

(江苏大学计算机科学与通信工程学院，江苏 镇江 212013)

1 概述

随着密码算法的完善，传统的线性和差分分析已经很难实现密码破译。而专用集成电路(Application Specific Integrated Circuit,ASIC)、现场可编程门阵列(Field Programmable Gate Array,FPGA)、数字信号处理(Digital Signal Processing,DSP)以及智能卡等密码算法芯片的大量普及应用，研究者越来越注意到利用实现和操作环境泄露的时间、能量、电磁等信息进行攻击的可能性。利用这些泄漏的信息对密码算法进行分析的方法称为侧信道攻击(Side Channel Attack,SCA)，其主要的攻击类型有时间攻击[1]和能量分析[2]攻击等。

RSA 算法作为公钥密码体系的核心算法之一，广泛应用于各种嵌入式密码系统，但其在实现过程中却易遭受侧信道攻击[3-4]。针对该问题，国内外研究人员提出了许多RSA的侧信道攻击及抗侧信道攻击方法[5-6]。文献[7]提出功耗轨迹分析方法和添加随机伪操作方法防御SCA，但该方法会泄露密钥中的部分比特位为0 的信息，且额外计算量较大；文献[8]提出等功耗编码方法能使算法效率提高，但全零段极易受到SCA，且增加了预计算过程；文献[9]改进了文献[8]全零段的抗攻击弱点，但预计算量仍未降低。本文对这些防御方法进行简单介绍，并针对时间和能量分析攻击，在改进的等功耗编码算法[9]的基础上，提出一种针对RSA抗侧信道攻击的改进窗口算法。

2 RSA 的实现算法及抗侧信道攻击分析

2.1 RSA 的实现算法

算法1 从左到右扫描的模幂(LR)M=Cdmod N

输入 正整数N，密文C，整数d=(dndn-1…d0)2

输出 M

2.2 RSA 模幂算法的侧信道攻击及其防御措施

由上述模幂运算过程可以看出，当d 的二进制bit 位为0 时，仅有平方操作；而d 的bit 位为1 时，运算过程包括平方和乘法操作，2 个不同bit 位运行时间存在明显差异。因此，可以利用密码算法执行时间差异进行时间攻击[1]。

能量分析攻击可以分为简单能量分析(Simple Power Analysis,SPA)攻击和差分能量分析(Differential Power Analysis,DPA)攻击。SPA 攻击在攻击者对算法本身特性有一定了解的前提下，通过观察功耗轨迹[7]，结合时间攻击，加之一定的经验来猜测密钥。差分能量分析攻击可以通过区分函数滤除伪操作和固定噪声，根据能量差分曲线是否会出现明显的尖峰来判断猜测的密钥是否正确，从而破译密钥[2]。LR 模幂算法16 位RSA 不同bit 位的功率轨迹如图1 所示。

图1 LR 模幂算法16 位RSA 不同bit 位的功率轨迹

对时间攻击应用最广泛的防御方法是盲化技术[10-11]，可以防止攻击者一位一位地进行分析。RSA 数据安全公司声称由于使用了盲化技术，运算性能降低了2%～10%。

对于能量分析攻击的防御，文献[7]提出添加随机伪操作方法，算法如下：

算法2 添加随机伪操作的从左到右扫描的模幂(LR)

输入 正整数N、W，密文C，整数d=(dndn-1…d0)2

输出 M

虽然算法2在运算效率上比直接添加伪操作的LR模幂运算算法有所提高[7]，但它的执行效率仍较低。因此，文献[9]在此算法及文献[8]的基础上提出了改进的等功耗编码算法[9]。

算法3 改进的等功耗编码算法

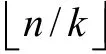
输出 M

Step1 预计算

Step1.1 R0←1

Step1.2 对于i 从1 增加到2k-1，执行：Ri←Ri-1×C mod N(有Ri=Cimod N)

Step2 M←1

Step3 对于j 从s 递减到0，执行：

Step3.1 M←M2kmod N

Step3.2 若dj≠0，M←M×Rdjmod N

否则，U←M×Rand(R)mod N

Step4 返回(M)。

其中，Rand(R)为余数表中的随机抽取的一个数。虽然算法3 解决了文献[8]中全零段抗攻击弱点，但预计算量仍未减少。

3 实现RSA 模幂运算的改进窗口算法

3.1 算法介绍

由于算法3 每次预计算是在前一个余数的基础上处理C 的一次方，产生连续余数表，因此所用的乘法为2k-3 个。研究后发现，可以对预计算过程进行优化，每次预计算处理C 的二次方，产生C 奇次幂的余数表，将乘法与求平方之间的平衡转换到更为有利的求平方过程中，只需要将预计算余数表中的奇次幂进行预先计算和存储。因此，本文算法的乘法仅需2k-1-1 个，预计算的乘法运算量减少了一半，使得RSA 实现过程在有效地抵御时间攻击和能量分析攻击的同时，能够提高运算速度。

算法4 从左到右的改进窗口模幂运算

输入 正整数N、k，密文C，整数d=(dsds-1…d0)b，dj=2hjuj，0≤j≤s，其中，uj是奇数；若dj=0，则hj=0,uj=0

输出 M

Step1 预计算

Step1.1 R0←1,R1←C,R2←C2mod N

Step1.2 对于i 从1 到2k-1-1，执行：R2i+1←R2i-1×R2mod N

Step2 M←1

Step3 对于j 从s 递减到0，执行：

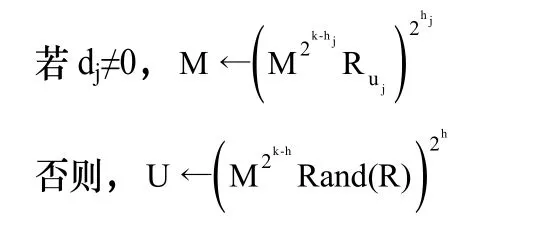
Step4 返回M。

其中，Rand(R)同算法3，为余数表中随机抽取的数；h 为1～(k-1)之间的随机数。

在算法3 中，当dj=0 时，计算结果存储到中间变量U中，不影响结果的输出；dj≠0 时，每轮迭代输出结果M =M2k×Rdj=M2k×Cdj。同理，在算法4 中，dj=0 时，计算结果也存储到中间变量U 中，不影响输出；dj≠0 时，得到M =M2k×(Ruj)2hj=M2k×(Cuj)2hj=M2k×C2hjuj=M2k×Cdj。2 个算法的输出结果一致，因此，算法4 是正确的。

3.2 改进窗口算法的蒙哥马利实现形式

由于除法运算比加减乘运算要费时得多，从降低或避免除法使用角度考虑，将算法4 与只需用乘法和数的位移就可实现模幂运算的蒙哥马利算法结合，从而得到算法5，进一步加快模幂算法的运行速度。

定义蒙哥马利约减为：MontRed(A,N,r)=Ar-1mod N；蒙哥马利模乘为：MontPro(A,B,N,r)=ABr-1mod N；其中，r=bn，bn-1≤N＜bn。

算法5 使用蒙哥马利实现的从左到右改进窗口模幂运算

输入 正整数N、k，密文C，d=(dsds-1…d0)b

输出 M

Step1 M←1

Step2 蒙哥马利运算预处理：

C←MontPro(C,r2mod N,N,r)=Cr mod N

M←MonrPro(M,r2mod N,N,r)=Mr mod N

Step3 预计算余数表

R1=C R2=MontRed(C2,N,r)

对于i 从1 到(2k-1-1)，执行R2i+1←MontPro(R2i-1,R2,N,r)

Step4 对于j 从s 递减到0，执行：

Step5 蒙哥马利运算后处理

M=MontPro(M,1,N,r)

Step6 返回M。

在算法5 中，由于存在预处理，经过蒙哥马利计算后得到的余数表为R1=Cr，R2=C2r，R2i+1=C2i+1r。当dj=0 时，计算结果存储到中间变量U 中，不影响结果的输出；当dj≠0时，每轮迭代输出结果：

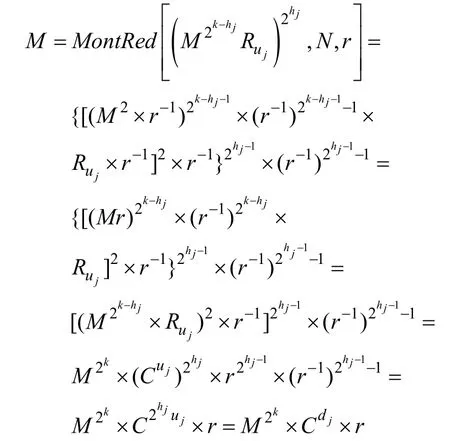
完成循环后，需进行蒙哥马利运算后处理，得M = M×1×r-1=(M2k×Cdj×r)×1×r-1=M2k×Cdj，算法5 的结果与算法4 一致，因此，算法5 是正确的。

4 改进窗口算法的抗计时和能量攻击分析

4.1 抗计时攻击分析

由算法5 可以看出，密钥被分为长度为k 的密钥段(最左边密钥段的长度在1～k 之间)。算法是对密钥段而不是密钥比特位进行迭代循环控制，因此，Kocher 的计时攻击是无效的。同时，在k 未知的情况下，计时无法直接确定循环的起点与次数，会增加攻击的难度。即使通过穷举搜索获取了k，但其密钥段对应2k种可能的密钥，而且k 长的dj=0 密钥段与dj≠0 密钥段对应的蒙哥马利操作数也一样，输出的中间结果都会存储到变量存储器中，避免了伪操作与真实算法操作之间的时间差异，使攻击者无法从操作时间上区分两者，弥补了文献[8]存在dj=0 密钥段攻击的缺陷，消除了分支结构导致的信息泄漏。因此，当k＞1 时，算法5达到了抗时间攻击的目的。

4.2 抗简单能量攻击分析

由算法5 的步骤4 可以看出，无论密钥段dj=0 或dj≠0都会在余数表中随机选取一个余数执行相同次数的蒙哥马利操作，其功耗情况在操作性上无法区分。加之电子噪声对轮迭代之间的干扰，攻击者无法直接通过功耗轨迹差异得出密钥段与轨迹图之间的关系，从而可以有效地抗SPA攻击，符合文献[12]静态掩盖算法抗SPA 攻击有效的结论。

4.3 抗差分能量攻击分析

DPA 攻击主要利用密码设备能量消耗的数据依赖性，通过差分将系统噪声、伪操作等剔除，获取密码算法中间值与功耗之间的相关性，进而得出密钥指数与相应的功耗轨迹的相关性。在算法5 中，当密钥段为dj=0 时，随机选取余数表中一个余数进行蒙哥马利运算，并将操作结果U存储到中间变量存储器中，其操作与真实操作一样，因此，不存在真正的伪操作，DPA 攻击不能鉴别出U，消除了上文提到的常规伪操作不储存结果对功耗曲线的影响。dj=0密钥段和dj≠0 密钥段都需要执行蒙哥马利运算和读取余数表操作，中间值都会进行存储，两者功耗无差别，显著地降低能量消耗的数据依赖性。算法5 消除了密钥指数段与功耗轨迹之间的相关性，使能量消耗独立于密码算法的中间值，因此，可以有效实现抗DPA 攻击。

5 改进窗口算法的防御效率分析

由于2 个不同数相乘可以表示为x×y=((x+y)2-(x-y)2)/4，因此一次快速乘法剩余的运算时间为平方剩余运算时间的2 倍。设密钥d 中“0”和“1”出现是等概率的，一次平方剩余运算时间为单位时间T，随机伪操作发生的概率为p。对于未添加伪操作的算法1 而言，平均需要n 次平方操作和n/2 次乘法操作，运算总时间T1为2nT；对添加随机伪操作的算法2，需要n 次平方操作和(1+p)×n/2 次乘法操作，运算总时间T2为(2+p)nT；对于改进的等功耗算法3，需要1 次平方和2k-3 次乘法预计算，sk 次平方和s 次乘法计算，运算总时间T3为{1+2(2k-3)+sk+2s}T；对于本文算法即算法4，需要1 次平方和2k-1-1 次乘法预计算，sk+hs次平方和s 次乘法计算，运算总时间T4为{1+2(2k-1-1)+sk+hs+2s}T，其中，0≤hs＜k。

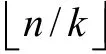
表1 各种防御算法总计算时间的比较

由表1 可以看出，在保证安全的前提下，算法4 较算法2 防御效率提高了36.8%，较算法3 提高了4%。

分析算法5 的模乘总计算时间。虽然算法5 采用蒙哥马利运算需要增加2 步预处理和1 步后续处理，但由于经典模乘法在进行迭代运算时，除了需要使用与蒙哥马利乘法相同的单精度运算外，还需要额外s 次的单精度除法，这开销随着s 增加而远大于蒙哥马利的预计算。因此，在s较大的情况下，算法5 可以大为减少模乘总计算时间，提高防御效率。

6 结束语

本文针对RSA 原有的抗侧信道攻击措施效率低的问题，在原有改进的等功耗编码防御方法基础上，提出一种改进窗口算法。将乘法与求平方之间的平衡转换到更为有利的求平方过程中，只需将预计算余数表中的奇次幂进行预先计算和存储。分析结果表明，该算法在保证安全性的前提下，可较大地提高运行效率。另外，如何设计一种有效防御复合侧信道攻击的RSA 算法是今后的研究方向。

[1]Kocher P C. Timing Attacks on Implementations of Diffie-Hellman,RSA,DSS,and Other Systems[C]//Proc. of CRYPTO'96. Santa Barbara,USA: Springer-Verlag,1996.

[2]Kocher P C,Jaffe J,Benjamin J. Differential Power Analysis[C]//Proc. of CRYPTO'99. Santa Barbara,USA:Springer-Verlag,1999.

[3]Perin G,Torres L,Benoit P. Amplitude Demodulation-based EM Analysis of Different RSA Implementations[C]//Proc. of Design,Automation and Test in Europe Conference and Exhibition. [S. l.]: IEEE Press,2012.

[4]王 敏,吴 震. 针对随机伪操作的简单功耗分析攻击[J].通信学报,2012,33(5): 138-142.

[5]张宝华,殷新春. RSA 密码算法的安全及有效实现[J]. 中山大学学报: 自然科学版,2008,47(6): 22-26.

[6]饶金涛,陈 运,吴 震,等. 一种抗简单功耗分析攻击的模幂算法[J]. 成都信息工程学院学报,2011,26(2): 123-126.

[7]韩 军,曾晓洋,汤庭鳌. RSA 密码算法的功耗轨迹分析及其防御措施[J]. 计算机学报,2006,29(4): 590-596.

[8]陈 运,吴 震,陈 俊,等. 防范边信道攻击的等功耗编码实现算法[J]. 电子科技大学学报,2008,37(2): 168-171.

[9]吴 震,陈 运,王 敏,等. 等功耗编码算法的改进实现及抗功耗分析攻击研究[J]. 通信学报,2010,31(8): 26-30.

[10] 陈财森,王 韬,田军舰,等. 一种针对RSA 算法软件应用的差分计时攻击[J]. 小型微型计算机系统,2011,32(4):672-675.

[11] 田军舰,田 颖,寇应展,等. 一种针对OpenSSL 中RSA的计时攻击改进算法[J]. 军械工程学院学报,2011,23(2):62-64,68.

[12] 吴 震,陈 运,陈 俊,等. 真实硬件环境下幂剩余功耗轨迹指数信息提取[J]. 通信学报,2010,31(2): 17-21.

[13] Denis T S. BigNum Math: 加密多精度算法的理论与实现[M]. 尹浩琼,译. 北京: 中国水利水电出版社,2008.