神经网络在加工误差控制中的应用*

乔培平

(陕西工业职业技术学院机械工程系，陕西咸阳 712000)

神经网络在加工误差控制中的应用*

乔培平

(陕西工业职业技术学院机械工程系，陕西咸阳 712000)

加工误差的控制是自动化加工技术中的难题，传统的控制理论不能解决一些问题。通过人工神经网络建立起切削加工自动控制系统，具体训练网络采用离线训练，将样本数据准备后用Matlab工具箱函数即可完成，并应用于实际的切削过程。结果表明，神经网络控制系统能有效的控制加工误差。

神经网络;加工误差;非线性系统;多输入输出

1 引言

人工神经网络是模拟人脑功能的非线性大规模并行信息处理系统，既具有专家系统的一切优点，又摒弃了常规方法所共有的缺陷。它具有很强鲁棒性、容错性，具有高度的自组织、自适应、自联想和自学习等能力。神经网络具有非线性特征:它具有逼近任意非线性函数的能力，这为具有非线性特征的机械加工过程提过了一种通用的系统辨识及控制方法。神经网络具有多输入输出特性:输入输出变量数没有限制，完全根据问题确定，因而为不同变量的系统提供了一种统一的处理方式。神经网络具有不同数据的融合能力，具有并行分布处理方式。神经网络是由神经元相互连接而成的，这种结构便于硬件实现。因此神经网络特别适合解决普通建模方法和传统人工智能难以解决的模式识别、非线性建模、图像处理、语言理解、联想记忆、自适应控制等问题。基于神经网络建立的切削加工自动控制系统具有更好的柔性、实时性以及便于实现智能控制等特点［4］。笔者介绍了在改装的CW6163车床上利用神经网络控制技术实现内燃机变椭圆活塞加工的加工精度控制问题。

2 ZQS700内燃机的变椭圆活塞及加工

活塞是内燃机的重要零件，为了改善活塞裙部与气缸间的贴合与润滑，确保活塞能良好的工作，活塞裙部的横向形状通常呈现椭圆形，且沿裙高方向截面的椭圆度是变化的，其轴向截面设计成中凸形。

变椭圆的外形面加工是一种典型的复杂形面加工问题。较为先进的加工方法是利用CNC的活塞外形面加工系统，利用该系统加工变椭圆活塞外形面时，提高加工精度仍存在较大难度。因为，常规的误差补偿和控制策略大多基于整个加工系统是线性、非时变和单输入、单输出系统的假设，这对简单形面的加工控制效果很好，但对象变椭圆活塞外形面加工这类多输入、多输出的非线性系统却难以奏效。基于传统单点补偿控制技术的实验表明，仅仅将形面上某点的加工误差反馈给加工系统以校正该点的输入，不仅被补偿点的加工精度没有达到预期效果，反而影响周围点的加工精度。鉴于此，变椭圆活塞外形面的加工误差控制，不能采用传统的单点补偿控制技术，而应采用适合于多输入多输出非线性系统的控制系统［2］。基于神经网络的控制，能对复杂形面的加工提供较为精确的控制。

3 神经网络控制原理

以车削一异形回转体为例，来说明神经网络的误差控制原理。图1中实线为一待加工的异形回转体。由于母线曲线未知，故可用母线上的n个离散点的横坐标及纵坐标(χi、yi)(i=1、2、……n)，来表示该回转体之理想形状，即yd=［y1、y2……yn］。

图1 待加工的异形的回转体

由于存在加工误差，这时加工出的回转体实际轮廓的n个离散点相应的坐标为(χi，yi')(i=1，2，……n)，且χi'=χi，如图2虚线所示。实际值可视为加工系统的输出，即y=［y1'，y2'……yn'］。如加工系统的输入为(χi，ui)，则该加工误差控制的实质就是，输入调整为多少值时，输出值与理想值相同或达到某个精度的逼近。

如果以U表示输入矢量U=［u1、u2……un］T，Y表示输出矢量Y=［y1'，y2'……yn'］T，则加工系统的输入输出非线性特性可描述为:

Y=G(U)

式中:G为系统的非线性传递函数，它把系统的输入映射为系统的输出。

Y=G(U)的含义为:给定输入U，可获得输出Y。然而，对于控制问题，并不需要这种映射关系。因为控制的任务是:给定一个系统的理想输出值Yd，系统的输入值Ud是多大?即我们感兴趣的是上述映射的逆映射:Ud=G－1(Yd)。利用神经网络实现从U－Y的正映射和从Y－U的逆映射是比较方便的，图2为系统逆模型的神经网络辨识示意图。

图2 神经网络辨识逆模型

图2仅表示神经网络辨识系统逆模型的原理图。具体训练网络时，采用离线训练，将样本数据准备后用Matlab工具箱函数即可完成。在样本数据中，网络输入数据为Y=［y1'，y2'……yn'］T，输出数据为U=［u1、u2……un］T。一旦神经网络的逆模型建立起来，就表明它具有从切削系统输出空间向输入空间进行逆映射的能力，将其作为切削系统的控制器来控制系统，系统就可以获得理想的输出。基于神经网络的控制系统原理图如图3所示。

从图3中可知，神经网络逆模型的输入为Yd，其输出为Ud=G－1(Yd);切削系统的输入是Ud，输出为Y=G(Ud)。由于神经网络逆模型是切削系统模型的逆映射，因此神经网络的传递函数G－1就是切削系统传递函数G的逆(G)－1，于是有:

上式表明，神经网络的输入为Yd，切削系统的输出也为Yd。因而，利用该控制系统原理，就可以获得期望的输出值Yd，这就是神经网络控制原理［1］。就本问题而言，期望的切削系统输出为Yd=［y1、y2……yn］，只需在神经网络输入端输入Yd，则加工出的工件尺寸将是理想或接近理想尺寸。

图3 控制系统原理图

4 控制系统的实现

图4为变椭圆活塞加工实验装置，机床为改装的CW6163机床。图4中步进电动机用于实现刀具横向精密微量进给，光栅长度测量仪测量凸轮推动摆杆支点的位移量。主控机根据不同误差补偿控制方式的活塞加工控制数据，与凸轮曲线数据比较，形成CNC控制文件。加工时，主控机先驱动步进电动机运转，然后根据光电开关1测量的凸轮转角信号，找到凸轮与活塞型线最佳的近似轮廓线，接着主控机以光电开关2测量的主轴回转信号，查阅CNC控制文件，发出相应的步进电动机控制脉冲，使步进电动机带动凸轮、摆杆推动刀具作相应的切削，从而实现凸轮曲线对中凸型线的拟合，完成其加工。

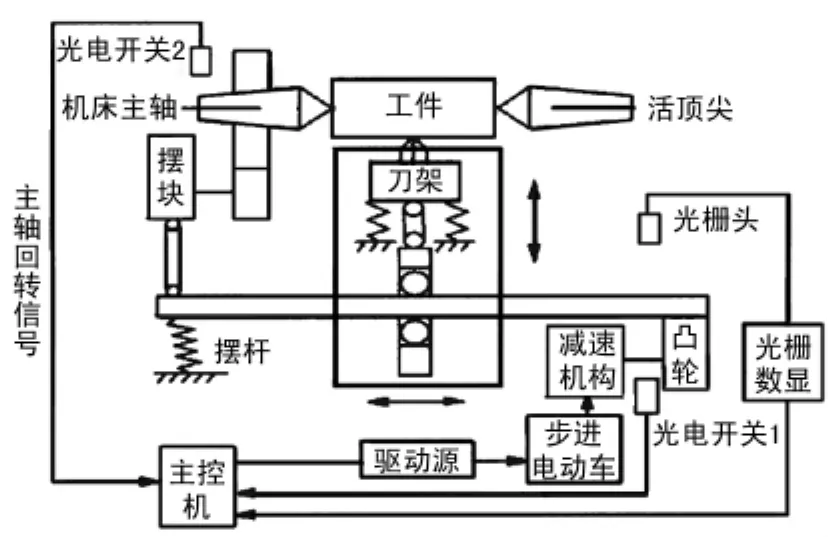
图4 变椭圆活塞加工实验装置示意图

5 测试结果及结论

采用传统误差补偿控制技术实施单输入单输出线性补偿时，加工出的工件实测值见表1中CNC加工栏，这时最大误差为11.3 μm。采用神经网络控制后，按神经网络提供的输入数据控制系统，加工实测值见表1中神经网络栏，这时最大误差为4.9 μm。由此可见，神经网络控制系统能有效地控制加工误差，神经网络应用于设备加工误差的控制有重要的理 论研究价值和广阔的应用前景。

表1 加工误差控制方法比较 /μm

［1］ 焦李成.神经网络的应用与实现［M］.西安:西安电子科技大学出版社，2003.

［2］ 尹红风.人工神经网络信息处理原理［M］.大连:大连理工大学出版社，1999.

［3］ 胡守仁.神经网络导论［M］.长沙:国防科技大学出版社，2005.

［4］ 孙宝元.切削状态智能监控技术［M］.大连:大连理工大学出版社，1998.

Neural Network Application in Machining Error Control

QIAO Pei－ping
(Mechanical Engineering Depantment，Shaanχi Industrial Vocational and Technical College，Xianyang Shaanχi712000，China)

Machining error control is one of the most difficult problems in automated processing technology，although the traditional control theory can not be solved，some problems.By artificial neural network，a machining automatic control system is established，the specific training network uses the offline training，after the sample data to be prepared for the Matlab，toolbox function can be completed，and applied to the actual cutting process.The results show that the neural network control system can effectively control the machining errors.

neural network;processing error;nonlinear systems;multiple input and output

TG702

A

1007－4414(2013)05－0079－02

2013－07－13

乔培平(1975－)，男，陕西咸阳人，讲师，主要从事设备控制技术、刀具切削状态智能监控技术方面的教学和研究工作。