集装箱正面吊变幅机构的铰点位置优化*

陈 桥，田明华

(1.湖南中铁五新重工有限公司，湖南长沙 410323;2.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083)

集装箱正面吊变幅机构的铰点位置优化*

陈 桥1，田明华2

(1.湖南中铁五新重工有限公司，湖南长沙 410323;2.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083)

集装箱正面吊变幅机构是正面吊大臂举升机构的核心，其变幅铰点位置的确定直接影响到整机的性能。通过对变幅机构受力特性的分析，以变幅油缸最大负载最小及变幅液压系统液压冲击最小为优化目标，建立变幅机构三铰点数学模型，采用分层排序法处理多目标问题的优化，利用Matlab粒子群算法对变幅铰点位置进行优化，结果表明优化后的铰点位置提高了正面吊整机性能，为变幅机构参数设计和改善提供了重要依据。

正面吊;变幅机构;Matlab粒子群算法;分层排序法

1 引言

集装箱正面吊(以下简称正面吊)是一种港口集装箱装卸、堆码和水平作业的特种工程设备，也用于铁路中专站和公路中专站的货物搬运。与叉车相比，它具有机动灵活，操作方便、稳定性好、堆厂利用率高等优势［1］。它主要由起重臂、车架体、轮胎、俯仰液压缸、伸缩液压缸、驾驶室、油箱、转向系统、液压系统、传动系统和吊具等组成［2］。

正面吊起升机构核心为三铰点变幅系统如图1所示，铰点位置的确定是正面吊整机设计的核心，直接关系到变幅油缸负载值及变幅系统压力冲击的大小，决定整机的稳定性和工作效率。

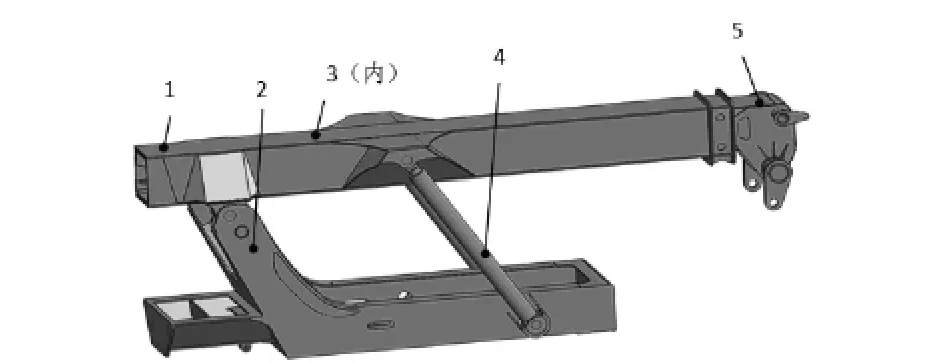
图1 正面吊起升系统组成

传统上变幅机构设计采用图解法，随着仿真学、遗传学和人工智能科学的发展，研究者们相继将遗传学、神经网络学原理应用到优化领域，结合计算机专业软件为正面吊变幅系统优化带来了新的方法［3］。笔者以变幅油缸最大负载最小及变幅液压系统液压冲击最小为优化目标，建立变幅机构的三铰点数学模型，采用分层排序法处理多目标问题的优化，利用Matlab粒子群算法工具箱对变幅系统铰点位置进行优化计算。

2 变幅机构运动及受力分析

正面吊起吊过程中，采用以变幅液压缸为主，伸缩液压缸为辅的主从模式进行协调控制［4］，使基本臂与伸缩臂联合运动，实现所起吊的集装箱垂直升降，提高了正面吊的工作效率。如图2，取正面吊臂架与车架体铰接点为原点建立坐标系，水平方向为χ轴，垂直方向为y轴。

油缸在变幅过程中，铰点B(χb，yb)沿BB'圆弧轨迹运动，臂架端部E(χe，ye)点即吊具重心垂直升降，A点为油缸下铰点，AB为变幅油缸，图中CE、CE'分别为臂架中心线在0度角和俯仰α角度的位置。臂架变幅过程中油缸受力为F，由于变幅过程中，速度比较慢，故不考虑臂架惯性力［5］。

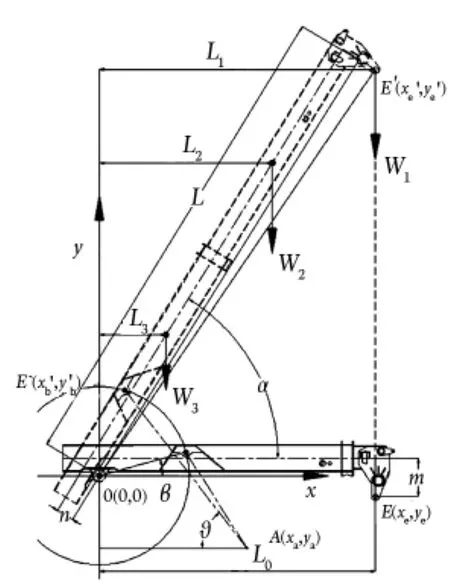
图2 变幅机构受力分析

式中:W1为吊重及吊具重;W2为伸缩臂及伸缩缸筒重;W3为基本臂与伸缩活塞重;F为俯仰油缸推力; L1为吊具及吊重力臂;L2为伸缩臂及活塞缸筒重力臂;L3为基本臂与伸缩活塞重力臂;n为俯仰油缸数量;φ1为起升冲击系数，取1.05;φ2为起升动载系数，取1.15;LP为俯仰油缸力臂。

根据臂架动力学分析可知，俯仰油缸运动过程中，F先变小，然后变大。当俯仰油缸下铰点A刚好在BB'连线上，俯仰油缸在水平位置和最大俯仰角αmax位置受力相等且为最大;当俯仰油缸下铰点A在BB'靠近原点一侧，油缸在最大俯仰角αmax受力最大;当俯仰油缸下铰点A在BB'远离原点一侧，油缸在水平位置受力最大。

3 优化设计目标函数

根据正面吊整机性能要求，选取变幅油缸最大负载最小及变幅液压系统液压冲击最小为优化目标进行设计优化。

3.1 设计变量

变幅系统三铰点有6个参数，选取其中一点为原点坐标，臂架在水平位置时，变幅油缸下铰点A(χa，ya)上铰点B(χb，yb)，考虑臂架实际空间位置及强度条件，变幅油缸上铰点距臂架中心线距离e作为常数处理，则本文引入3个优化参变量，其向量表达式如下:

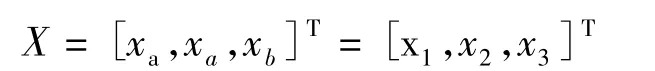
3.2 目标函数

(1)变幅油缸受力F可由给定的设计变量表示

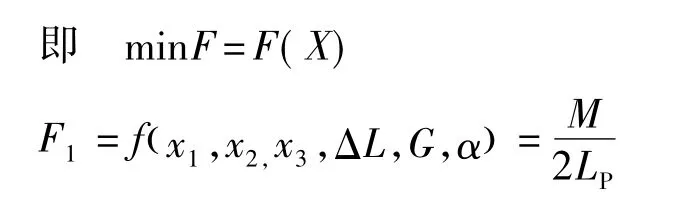
(2)液压油波动分析

变幅油缸最大工作压力Pmax＜Pmax'，在变幅过程中，根据油缸最大压差来衡量液压油的波动:

4 约束条件

(1)自变量上下限约束

根据实际问题要求，自变量有上下限的约束，即

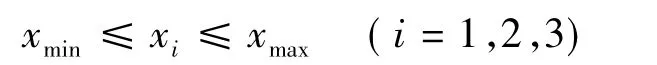
根据铰点空间位置选取自变量值域如表1所列。

表1 正面吊变幅铰点优化参数及可行域 /mm

(2)铰点位置约束条件

在变幅铰点优化之前，三个铰点位置无法确定，可根据臂架实际运动情况大致确定三个铰点的相对位置，如图2所示，该结构采用前支式三铰点，则铰点位置有如下约束条件:

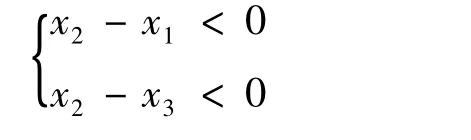
(3)油缸尺寸约束

为了保证油缸稳定性，需要对油缸长度尺寸进行约束，臂架在αmin到αmax俯仰过程中，油缸伸缩比λ= Lmax/Lmin，考虑到俯仰油缸制造问题，根据油缸设计规范，取液压油缸的伸缩比λ值为1.6≤λ≤1.7，得到约束条件如下:

(4)机构几何尺寸约束条件

伸缩臂位置在0°和60°典型位置上时，三铰点组成ΔOAB、ΔOAB'中，由两边之和大于第三边得到6个约束条件:

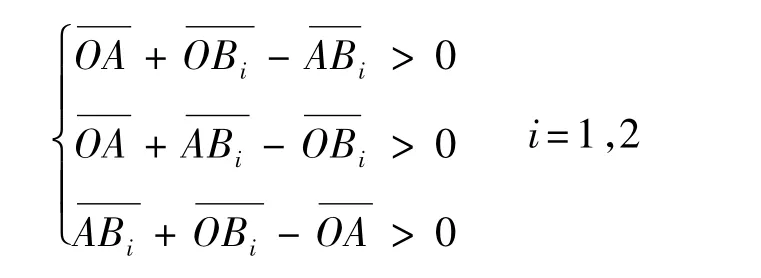
5 优化结果及分析

首先，将目标函数按照其重要性排序，俯仰油缸俯仰过程中受最大力最小为该多目标优化问题的关键，液压油波动问题是在俯仰油缸受力最小的基础上考虑的，则求解优先顺序minF=F(X)优于minF= Fmax(X)－Fmin(X)，正面吊在最大变幅角度受力最大，以该工况为研究对象进行优化计算。由于非线性约束问题最优解与其初始值的选取密切相关，不同的初始值会得到不同的局部最优解［6］;而正面吊变幅三铰点的可行解空间的确定是经过人工经验和单个变量参数反复优化才得到的数据，以WX45T型正面吊实际设计参数进行变幅三铰点优化仿真，采用粒子群算法工具箱进行优化计算，其主要优化参数选取:维数D=3;粒子数目N=100;最大迭代次数M=1 000;最大速度Vmax=1;学习因子C1、C2均为1.5;惯性权重Wmax=0.8、Wmin=0.2，其它基本参数见表2。

表2 正面吊变幅铰点优化基本参数

图3为俯仰油缸受载迭代收敛曲线，采用Matlab数学软件优化分析，得到正面吊臂架在最大仰角αmax位置处，各自变量与俯仰油缸载荷关系如图4～6所示。

图3 俯仰油缸受载迭代收敛曲线

通过对图4～6进行分析可知，臂架在最大仰角位置时，对俯仰油缸载荷影响最大的是自变量χ1、χ3，影响最小的是χ2，图4表明，俯仰油缸载荷随χ1增大近似比例减小;图5显示，χ2对俯仰油缸载荷影响较小，趋于线性关系;俯仰油缸载荷随着自变量χ3先减小，然后缓慢最大，且在2 615 mm处取得最小值，该参变量是臂架在最大仰角位置处俯仰油缸载荷关键影响因素。

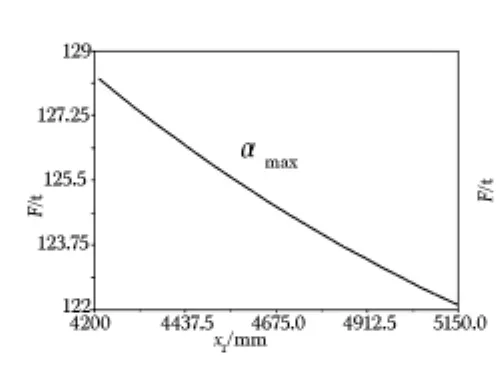
图4 油缸负载与χ1之间的关系

图5 油缸负载与χ2之 间的关系

通过Matlab粒子群算法工具箱进行优化计算，得到3个铰点最终优化结果，如表3所示。

表3 变幅机构参数优化后三铰点参数值

图7为优化前后俯仰油缸在最大仰角位置处受力与臂架俯仰角度之间变化关系曲线图。

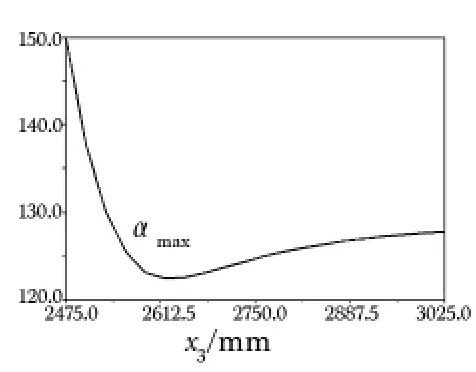
图6 油缸负载与χ3之间的关系

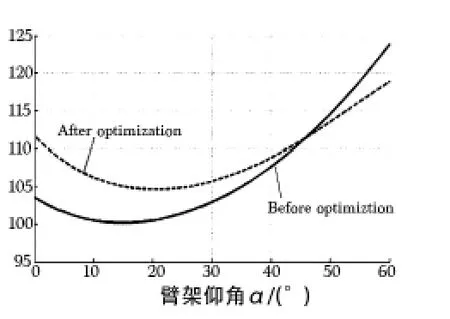
图7 优化前后俯仰油缸受 力与角度变化关系

通过对图形分析，俯仰油缸载荷先减小后增大，优化后，在臂架水平位置，俯仰油缸载荷增加4.8%，最大载荷仍然出现在臂架最大仰角位置处。优化前后对比，俯仰油缸受最大力相对于初始设计值降低了5.77%，压力波动值降低9.51%，如表4所示。

表4 优化前后俯仰油缸受力值

通过对变幅机构铰点位置参数进行优化，使臂架在最大仰角位置处俯仰油缸受力明显降低，同时优化结果使俯仰油缸在变幅过程中，最大受力与最小受力差值减小，使变幅系统压力变化趋于平稳，大幅度提高了正面吊起升机构的动态性能，改善了臂架结构受力特点，使臂架与油缸铰点处极限载荷降低。

［1］ 彭传圣，苏国萃.集装箱正面吊吊运机应用与发展［J］.装卸机械，2001(3):30－32.

［2］ 张连文.集装箱正面吊运机的ADAMS运动学分析［J］.工程机械，2007，38(7):19－21.

［3］ 冯 谦.伸缩臂装载机变幅机构的优化没计［J］.南京林业大学学报，1993，17(1):65－68.

［4］ 刘 宜，方 静.基于主一从模式的正面吊垂直升降协调控制方法［J］.中国工程机械学报，2011，9(2):181－184.

［5］ 曾立斌，候钟明.伸缩臂叉装车铰点位置的优化设计［J］，起重机运输机械，2008(3):22－25.

［6］ 张 武.MATLAB优化工具箱及其应用［J］.农业网络信息，2008(8):138－142.

Optimization of the Hinge Point Position of Leveling Mechanism for Reach Stacker

CHEN Qiao1，TIAN Ming－hua2
(1.China Railway Wuχin Heavy Industry Co.，Ltd，Changsha Hunan 410323，China;2.Key State Laboratory of
High Performance Compleχ Manufacturing，Ministry of Education Central South University，Changsha Hunan 410083，China)

The luffing mechanism of reach stacker is the core of arm luffing mechanism.Therefore，the hinge point's positions of leveling mechanism directly affects the whole performance.Through the force analysis of luffing mechanism，a mathematical model of three hinge points is established，which aims to reduce the max force of oil cylinder and decrease the oil pressure of oil system.The paper deals with multi－objective optimization problem by using hierarchical ordering method.The optimization calculation is presented by using the particle swarm optimization of Matlab.The results indicate that the optimized result can enhance the performance of the reach stacker.

reach stacker;luffing mechanism;the particle swarm optimization of Matlab;Hierarchical ordering method

TH213.6

A

1007－4414(2013)05－0031－03

2013－07－28

陈 桥(1983－)，男，贵州沿河人，工程师，主要从事港口起重机方面的设计研究工作。