冻融环境下变形钢筋与混凝土间黏结应力计算模型
2013-06-07谢晓娟
王 青,卫 军,徐 港,谢晓娟
(1.中南大学土木工程学院,湖南长沙 410075;2.三峡大学土木与建筑学院,湖北宜昌 443002)
冻融环境下变形钢筋与混凝土间黏结应力计算模型
王 青1,2,卫 军1,徐 港2,谢晓娟2
(1.中南大学土木工程学院,湖南长沙 410075;2.三峡大学土木与建筑学院,湖北宜昌 443002)
D OI:10.3880/j.issn.10067647.2013.01.007
为研究冻融作用对钢筋混凝土无箍筋试件黏结强度的影响,引入相应的损伤变量对Hsieh-Ting-Chen四参数混凝土破坏准则进行修正,确定冻融损伤下的混凝土破坏准则,建立冻融环境下黏结失效的理论计算模型。通过对钢筋肋间混凝土在挤压力、摩擦力等作用下的受力分析,给出冻融环境下变形钢筋与混凝土之间极限黏结应力的计算方法及锥面斜角、摩擦因数等参数的取值,详细阐述了极限黏结应力的求解思路。利用已有文献试验结果对该理论计算模型进行验证,结果表明冻融次数在一定范围内计算值与试验值吻合较好,模型精度较高。
混凝土结构;变形钢筋;黏结应力;冻融作用
处于北方寒冷地区的钢筋混凝土结构常常由于冻融作用引起耐久性劣化,导致建筑物提前发生破坏。国内外学者的相关研究成果表明,冻融作用是寒冷地区影响混凝土结构耐久性的重要因素,它不仅会降低混凝土的强度,而且对钢筋与混凝土之间的黏结性能有着重要影响。钢筋与混凝土之间的黏结力是二者能够共同工作的基础,Shih等[1-13]研究了冻融循环对钢筋与混凝土黏结性能的影响,得出了一些定性的结论,但是,冻融作用造成钢筋与混凝土黏结性能退化的计算模型在国内外却鲜有报道。该模型的研究对于钢筋混凝土结构在冻融环境下力学性能退化的理论和数值分析具有重要意义,同时也为完善受冻害地区钢筋混凝土结构的耐久性设计、评估和维修加固提供了必要的依据,具有重要的理论和实际意义。
1 黏结失效模型及应力状态
1.1 理论模型
变形钢筋与混凝土黏结破坏过程一般可分为微滑移段、滑移段、劈裂段、下降段及残余段5个阶段,对于无箍筋试件劈裂段即为其极限黏结应力对应的阶段。文献[14]对变形钢筋与混凝土黏结性能的试验研究和理论分析表明,黏结劈裂破坏可用如图1所示的劈裂-极限受力模型描述,并具有以下特点:变形钢筋受力后横肋挤压混凝土,使肋的背面与混凝土脱离形成裂缝,该裂缝向肋顶延伸形成肋顶斜裂缝,发展到约2倍肋高处停滞,此时斜裂缝及向前延伸的不可见微裂缝将握裹层混凝土切割成一系列斜向受压的圆锥状筒体,并在筒顶承受横肋斜向挤压,随着荷载的增大,钢筋横肋前的混凝土压碎堆积并挤压成楔状,形成新的挤压和滑移面,如图1所示,继续加载将发生劈裂破坏。假设试件经冻融后劈裂破坏特征不发生变化,根据上述特点,可采用劈裂-极限受力模型推导黏结失效的劈裂强度。

图1 劈裂-极限受力模型
当钢筋与混凝土发生相对滑动后,钢筋与混凝土之间的黏结力主要为机械咬合力,基圆部分与混凝土之间的胶着力和摩擦力影响较小,该部分作用忽略不计。锥楔挤压面的受力状态如图2所示,即在横肋前方的挤压力pj和横肋上的摩擦力fpj(f为挤压面和滑移面间的摩擦因数)。由于力的斜向作用使周围混凝土产生了径向压应力σr和环向压应力σθ。

图2 劈裂应力状态受力示意图
如图2(a)所示,将钢筋相邻两肋间的混凝土斜向压肢进行受力分析:将pj和fpj分别向混凝土咬合齿根截面投影,可得A点径向压应力σr和平均剪应力τ分别为


式中:γ为pj与斜裂缝的夹角;α为锥面斜角;β为肋顶斜裂缝倾角;Aj为锥楔挤压面面积;Ac为混凝土咬合齿根部(A点)的面积;d′、l、h分别为基圆直径、横肋间距和横肋高度,对于月牙纹钢筋,当钢筋直径为d时,d′=0.96d,l=0.6d,h=0.07d。
根据文献[14]提出的锥楔作用和环向应力梯形分布假定,可求得钢筋与混凝土交界面上的平均径向推力pt引起的混凝土咬合齿根部环向压应力σθ满足式(3):

式中:Kθ为环向应力系数,取决于相对保护层厚度c/d。
将pj、fpj分别向水平方向投影,可得发生劈裂破坏时的黏结应力τcr:
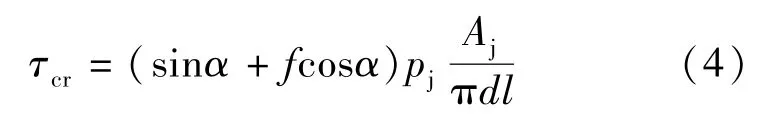
由式(4)知,如能确定pj和f,便可得到无横向约束钢筋混凝土试件的极限黏结应力。
1.2 参数的确定
a.α的确定。α的变化范围通常在10°~40°之间,未冻融前取平均值25°[14],随着冻融次数的增加,肋前堆积楔增多,α有增大趋势,假定混凝土强度降幅达1/3时对应的α为40°,其间按照线性内插,即

式中:fcu为冻融前混凝土立方体抗压强度;f′cu为冻融后混凝土立方体抗压强度。
b.β的确定。β主要与钢筋肋面倾角及钢筋与混凝土之间的摩擦因数有关,可由式(6)确定[14]:

式中:φ为钢筋肋面倾角,对于月牙纹钢筋,φ=π/4;μ为钢筋与混凝土之间的摩擦因数,一般可取0.213[15]。
c.f的确定。混凝土结构未损伤时f可取0.6[14],随着冻融次数的增大,f略有减小,但由于缺少实测资料,暂取为常数0.6。
2 冻融环境下的破坏准则和强度计算
混凝土斜向压肢上共有4种作用力,但独立变量只有pj。混凝土咬合齿根部处于复杂应力状态,因而应用多轴强度破坏准则判定混凝土是否破坏,通过求解混凝土强度准则公式即可得到pj。
2.1 混凝土多轴强度破坏准则
混凝土多轴强度破坏准则很多,但一般研究认为四参数、五参数准则能较全面地反映混凝土破坏曲面的特征[16],如文献[14]在分析无锈蚀钢筋黏结破坏特征时选用的是Ottosen四参数准则;文献[15]在分析锈蚀变形钢筋与混凝土的黏结应力模型时采用了Hsieh-Ting-Chen四参数准则。在比较分析多个破坏准则的基础上,笔者认为Hsieh-Ting-Chen四参数准则简洁,求解效率及精度较高。
Hsieh-Ting-Chen四参数准则[17]的表达式为

式中:fc为混凝土轴心抗压强度;参数k1~k4由试验确定,k1=2.010 8,k2=0.971 4,k3=9.141 2,k4= 0.2312;σ1为第一主应力;I1、J2分别为应力张量第一不变量和应力偏量第二不变量。
2.2 混凝土冻融损伤破坏准则
理论及试验研究表明,随着冻融次数的增多,不仅降低了混凝土强度,而且也改变了破坏准则。在冻融环境下,混凝土结构遭受反复冻融损伤,内部产生微裂纹并残留不可逆的残余膨胀变形。用D1和D2分别表征冻融后的体积损伤和畸变损伤,将混凝土内部损伤完全由冻融后的弹性模量和泊松比来表征[18]:

式中:E、分别为混凝土无损状态和冻融后的弹性模量;ν、分别为混凝土无损状态和冻融后的泊松比。
若假定冻融循环作用后混凝土仍然具有无损材料破坏面的特点,则由塑性力学基本原理,应用Cauchy应力不变量分别表示相应的有效应力不变量:

结合式(8),可得


要求解式(10),首先应求得各应力不变量,而由经典力学理论有

各主应力(σ1、σ2、σ3)与混凝土齿根部A点的应力(σr、σθ、τ)有如下关系:

将式(11)~(15)代入式(10),将式(1)~(3)代入式(10)可求出pj,再将求出的pj代入式(4)便可得到发生劈裂破坏时的黏结应力τcr。
3 试验验证
文献[19]采用中心拉拔试验对冻融作用后的黏结性能进行研究,采用该文献的试验数据对本文所建模型的适用性进行验证。该试验测得的冻融前混凝土立方体抗压强度平均值为30.71 MPa,冻融循环15次、30次、50次后混凝土立方体抗压强度平均值分别为25.86 MPa、23.20 MPa、20.00 MPa。
假设经受冻融循环作用前后混凝土的轴心抗压强度及弹性模量与立方体抗压强度间的换算关系不变,则可基于式(16)~(17)由不同冻融循环作用后的立方体抗压强度实测值换算得到冻融后的混凝土轴心抗压强度和弹性模量:

基于以上材料参数,按前述理论编程计算出极限黏结应力,并与文献[19]中的实测值进行比较,如表1所示。

表1 冻融后极限黏结应力计算值与实测值的比较MPa
分析表1中数据可知,计算值与实测值较为接近,进一步计算可得3组数据的相关系数分别为0.9719、0.9682、0.993 2,说明相关性良好,该模型精度较高。
4 结 论
a.在引入冻融损伤变量和冻融损伤演化方程的基础上,对Hsieh-Ting-Chen四参数混凝土破坏准则进行修正,得到了混凝土冻融损伤破坏准则。
b.以无横向约束的变形钢筋混凝土试件为研究对象,建立了冻融环境下黏结失效的理论计算模型,得到了冻融环境下变形钢筋与混凝土之间极限黏结应力的计算方法,并给出了锥面斜角、摩擦因数等参数的取值。
c.利用文献[19]的中心拉拔试验结果对该模型进行验证,结果表明,当冻融次数在一定范围内(混凝土强度降幅在1/3以内时)模型计算值与试验实测值较为接近且相关性良好。
[1]SHIH T S,LEE G C.Effect of freezing cycles on bond strength of concrete[J].Journal of Structural Engineering, 1988,114(3):717-726.
[2]张燕,曹大富.冻融循环对钢筋与混凝土黏结性能的试验研究[J].山西建筑,2007,33(31):73-74. (ZHANG Yan,CAO Dafu.Experimental research on the bond performance between reinforcing bars and concrete during freeze-thaw cycle[J].Shanxi Architecture,2007, 33(31):73-74.(in Chinese))
[3]赵娟,邹超英.冻融作用后钢筋与混凝土之间黏结性能研究[J].沈阳建筑大学学报:自然科学版,2007,23 (5):719-722.(ZHAO Juan,ZOU Chaoying.Study on bonding property between steel rebars and concrete caused by freeze thaw action[J].Journal of Shenyang Jianzhu University:Natural Science,2007,23(5):719-722.(in Chinese))
[4]GUO Yuxia,GONG Jinxin.Degradation of bond between steel bar and freeze-thaw concrete after electrochemical chloride extraction[J].Journal of Central South University of Technology,2010,17(2):388-393.
[5]赵娟,巴恒静,邹超英,等.冻融环境下钢筋混凝土间黏结界面的显微结构[J].武汉理工大学学报,2009, 31(19):78-80.(ZHAOJuan,BAHengjing,ZOU Chaoying,etal.Microstructureofbondinginterface betweenreinforcementandconcreteinfreeze-thaw environment[J].JournalofWuhanUniversityof Technology,2009,31(19):78-80.(in Chinese))
[6]冀晓东,宋玉普.冻融循环作用后钢筋与混凝土黏结性能试验研究[J].大连理工大学学报,2008,48(2): 240-245.(JIXiaodong,SONGYupu.Experimental research on bond behaviors betweensteelbarsand concrete after freezing and thawing cycles[J].Journal of Dalian University of Technology,2008,48(2):240-245. (in Chinese))
[7]周志云,孙敏,吕礼春.混凝土冻融变形的试验研究[J].混凝土,2010(4):20-27.(ZHOU Zhiyun,SUN Min,L¨U Lichun.Deformations of concrete under different freeze-thaw test conditions[J].Concrete,2010(4):20-27.(in Chinese))
[8]牛荻涛,肖前慧.混凝土冻融损伤特性分析及寿命预测[J].西安建筑科技大学学报:自然科学版,2010,42 (3):319-322.(NIU Ditao,XIAO Qianhui.Analysis of cumulative damage characteristics and life prediction for the concrete in freezing-thawing circumstance[J].Journal of Xi'an University of Architecture&Technology: Natural Science,2010,42(3):319-322.(in Chinese))
[9]KAMYAB Z H,PETER U,KARIN L.Experimental study of the material and bond properties of frost-damaged concrete[J].Cement and Concrete Research,2011,41 (3):244-254.
[10]SHUI Z H,XU H G,ZHAN B J.Freeze-thaw resistance of concrete in seawater[J].Journal of Wuhan University of Technology,2010,32(17):108-111.
[11]LASSE P,LUDGERL,MARIAAP.Influenceof freezing-and-thawing damage on behavior of reinforced concrete elements[J].ACI Materials Journal,2007,104 (4):369-378.
[12]CHO T J.Prediction of cyclic freeze-thaw damage in concrete structures based on response surface method[J]. Construction and Building Materials,2007,21:2031-2040.
[13]孙景路,刘丽佳,程卫国.冻融循环对混凝土铰接板摩擦性能的影响[J].水利水电科技进展,2009,29(增刊1):239-240.(SUN Jinglu,LIU Lijia,CHENG Weiguo. The impactoffreeze-thawcycleonperformanceof concrete hinged-plate friction[J].Advance in Science and Technology of Water Resources,2009,29(Sup1):239-240.(in Chinese))[14]徐有邻.变形钢筋-混凝土黏结锚固性能的试验研究[D].北京:清华大学,1990.
[15]徐港,卫军,王青.锈蚀变形钢筋与混凝土黏结应力模型研究[J].工程力学,2008,25(12):123-126.(XU Gang,WEI Jun,WANG Qing.Modelling bond strength of corroded deformed bar in concrete[J].Engineering Mechanics,2008,25(12):123-126.(in Chinese))
[16]江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005.
[17]HSIE S S,TING E C,CHEN W F.Plasticity-fracture model for concrete[J].International Journal of Solids and Structure,1982,18(3):181-197.
[18]唐光普,刘西拉.混凝土冻融损伤破坏面的研究[C]//邢峰.沿海地区混凝土结构耐久性及其设计方法.北京:人民交通出版社,2004.
[19]冀晓东.冻融后混凝土力学性能及钢筋混凝土黏结性能的研究[D].大连:大连理工大学,2007.
A model of calculating bond strength between deformed bar and concrete in freeze-thaw environment
//WANG Qing1,2,WEI JUN1,XU Gang2,XIE Xiaojuan2(1.College of Civil Engineering,Central South University,Changsha410075,China;2.College of Civil Engineering and Architecture,China Three Gorges University,Yichang443002,China)
The influence of freeze-thaw action on the bond strength between reinforcing steel bars and concrete without stirrups was investigated,and the damage variables were introduced to modify the four-parameter Hsieh-Ting-Chen failure criterion of concrete.Based on it,the failure criterion of concrete in a freeze-thaw environment was determined,and a theoretical model for the bond failure after freezing and thawing was proposed.Based on stress analysis of the concrete corbel between the ribs under normal compressive pressure and friction pressure,a method of calculating the ultimate bond strength between deformed bars and concrete in a freeze-thaw environment was deduced,and the parameters such as the oblique angle on the cone surface and friction coefficient were determined.In addition,the solution procedure of the ultimate bond strength is illustrated in detail.The theoretical model is verified by test results from some existing literatures, and it can be concluded that,within a certain range of freeze-thaw cycles,the calculation results of this model are in good agreement with the test results,and that the accuracy of the model is high.
concrete structure;deformed bar;bond strength;freeze-thaw action
TU432
A
10067647(2013)01003304
2012-04-18 编辑:骆超)

国家自然科学基金(51109121,51174291);中国水利水电科学研究院开放基金(IWHRKF201009)
王青(1976—),女,江苏无锡人,副教授,博士研究生,主要从事混凝土结构耐久性研究。E-mail:postwq@163.com
