山区宽窄相间河道平面二维水流数值模拟

周苏芬,易子靖,闫旭峰,杨青远,2,王协康

(1.四川大学水力学与山区河流开发保护国家重点实验室,四川成都 610065; 2.香港城市大学土木与建筑工程系,香港 310027)

山区宽窄相间河道平面二维水流数值模拟

周苏芬1,易子靖1,闫旭峰1,杨青远1,2,王协康1

(1.四川大学水力学与山区河流开发保护国家重点实验室,四川成都 610065; 2.香港城市大学土木与建筑工程系,香港 310027)

针对山区河道受地质条件及河床演化的影响,其平面形态常呈现宽窄相间的渐变形态特征,采用贴体坐标法剖分正交贴体曲线网格求解域,用有限体积法离散控制方程,以SIMPLER计算程式求解耦合方程,建立山区宽窄相间河道平面二维水流数学模型。将模型计算值与宽窄相间水槽水流试验实测值及水动力学SMS软件计算结果进行比较,结果表明:该模型能够较好地模拟宽窄相间河道平面二维水流运动特性,宽窄相间河道河宽渐变将引起水深和流速的变化,在河道最窄处水深降到最低,流速最大;在河道最宽处水深达到峰值,流速最小。

宽窄相间河道;平面二维数值模拟;贴体坐标;有限体积法;SIMPLER算法

山区河流在峡谷地区受地质条件约束,经过极长时间调整常形成宽窄相间形态,如岷江金马河段最宽处为1010m,而其他地方河宽多在300～600 m之间。宽窄相间的平面形态显著影响河道水沙运动及其演化特性。Lucy等[1]基于野外调查认为河道宽度变化是影响河床演化的关键因素之一。Singha等[2]基于试验指出,河道形态变化将重新调整水流紊动能的分布特性。Armellini等[3]基于数值计算得出,受岸滩形态的影响,水流结构出现极为明显的分离区。Paiement-Paradis等[4]通过试验表明河道宽窄变化引起的水流减速或加速运动对泥沙推移质输移有重要影响。闫旭峰等[5]基于室内试验指出渐变河道形态显著影响宽窄相间区域的局部水头损失。

目前,平面二维水流数学模型得到了较成熟的发展,为利用数值模型研究宽窄相间河道的水流特性奠定了较好的基础。早期有荷兰德尔夫特水力研究所的RIVMOR 2D模型,美国爱荷华大学水利所的MOBED2模型,德国卡尔斯鲁厄大学的FAST2D模型及美国陆军工程兵水利工程实验室和杨百翰大学等合作开发的水动力学SMS模型及丹麦水利所的MIKE21模型。Arruda等[6-8]将IB法(Immersed boundary method)应用于平面二维水流数值模拟计算中,并取得了较好的结果。李大鸣等[9]考虑上、下游洪水边界的控制条件及糙率随河道流量变化的调整,提出了河道洪水演进的二维水流数学模型的计算方法。张细兵等[10]采用质量集中的简化处理和预估校正的时间推算法,较好地解决了平面二维水流泥沙数值求解的速度问题。张大伟等[11]通过有限体积法建立了反映大坝瞬时溃决水流特点的数学模型,并以Malpasset水库对模型进行验证。叶如意等[12]利用平面二维水动力学模型对曹娥江至宁波的引水工程进行模拟,同时对模型进行验证和优化。方神光等[13]结合纯隐格式的混合有限分析法及干湿判别标准与冻结法建立了二维水流数学模型并将其应用于实际工程中,取得了较准确的计算结果。王君超[14]利用有限体积法建立了平面二维水沙数值模型,计算结果能较好地反映天然河床的变形规律。为了更深入地探讨宽窄相间河道的水流特性,本文在前人研究的基础上,以宽窄相间水流运动为研究对象,通过室内水槽试验及数值模拟,进一步研究平面二维水流模型以模拟山区河道水流的运动特性。

1 正交贴体曲线网格的生成

采用椭圆形方程法生成二维正交贴体曲线网格,为避免产生波状速度场,动量方程的离散采用交错网格体系,即将流速布置在控制体积的交界面上,与水深、水位等错开半个网格。

物理平面上的不规则区域与计算平面上的规则区域之间的坐标变换满足Possion方程:

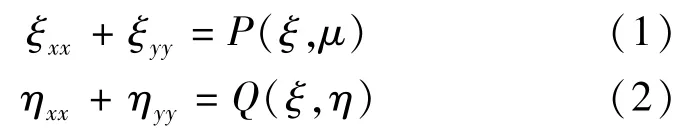
式中:x、y为笛卡儿坐标系下求解域网格节点坐标;ξ、η为贴体坐标系下求解域网格节点坐标;P、Q为调节因子,即网格密度控制函数,其作用是调节网格线位置的变化,使网格的疏密根据需要分布并可使变换后的网格曲线更好地拟合边界,保证正交,P、Q采用Thompson等[15]建议的函数表达式。

通过求解Possion方程生成试验渐变河段网格,见图1。

2 山区河道平面二维数值模型

2.1 控制方程

针对山区河道渐变特点,采用贴体坐标法对生成的二维正交贴体曲线网格求解域进行剖分,利用有限体积法离散控制方程,以SIMPLER计算程式求解耦合方程。

将水流连续方程和动量方程写成统一的偏微分方程:

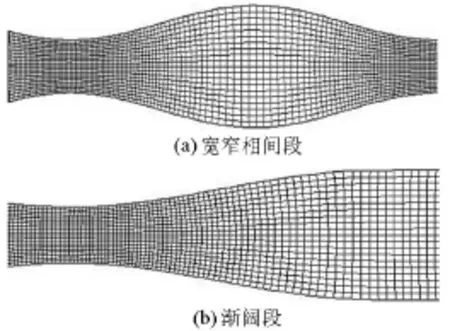
图1 试验渐变河段网格

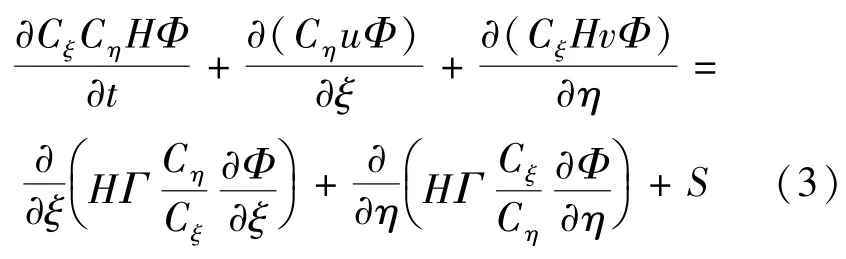
式中:Cξ、Cη为拉梅系数;H为水深;Φ为通用变量;t为时间;u、v分别为x、y方向的流速;Γ为扩散系数;S为源项。

对S进行负坡线性化处理,即S=SC+ΦOSO(SC为源项的常数部分;SO为系数;ΦO为中心点的变量)。根据有限体积法,将通用偏微分方程(式(3))在控制体积内积分,得到离散方程如下[16]:

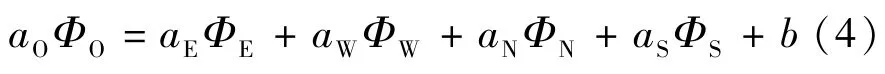
式中:a为系数;Φ为节点处变量;b为相邻节点变量与源项产生的常数;下标O、E、W、N、S表示节点位置,O表示中心点,E、W、N、S分别表示东、西、北、南节点。

离散格式采用的是由Patankar[17]提出的幂函数格式,则表示如下:

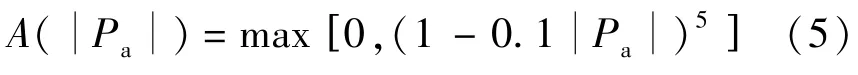
式中:Pa为派克里特数,为对流强度与扩散强度之比。

计算初始流速场为零,初始水位场根据已知进出口断面初始水位内插出求解域中各点的初始水位,断面不考虑横比降。计算河段进口边界给定流量,下游出口边界给定各点水位过程线。

2.2 模型的建立

基于Visual C++语言建立平面二维水流数值模型,模型涉及的主要变量和参数有各点水流流速u、v,床底高程zb,水位z,初始流速u0、v0,初始水位z0,各网格点x、y、z坐标,正交曲线坐标系中的拉梅系数Cξ、Cη及河床的糙率n。

3 模型的验证与计算

通过模型计算、试验测量以及SMS软件[5]计算结果的比较来验证模型的可靠性,其中,SMS软件计算数据采用文献[5]中的计算成果。

3.1 SMS软件

SMS软件包括RMA2、TABS-MD、AD-CIRC、CGWAVE、STWAVE、HIHEL等计算模块。RMA2是一个沿水深积分后平均的二维有限元水动力数值模型,可以用于计算具有自由表面缓流的水面高程、水深、平面流速的二维流场,适用于恒定流和非恒定流。该模块根据Galerkin的残值权重理论的有限元法及Newton-Raphson迭代法求解,再根据Navier-Stokes方程推求水深,其中综合糙率用曼宁公式计算。RMA2基于静水条件假定运行,并忽略重力方向的平均加速度,它仅局限于水平面上的二维数值模拟。

3.2 试验工况

宽窄相间河道模型水槽位于四川大学山区河流开发保护国家重点实验室模型实验场A区的渐变水槽自循环系统中(图2)。水槽内壁采用水泥光滑抹面,糙率为0.013。水槽全长28 m,坡度为0.2％。水槽进口断面处为砖砌花墙,能起到平缓水流的作用;花墙距离渐变起始点5.5m;最后一个最窄断面至水槽末端7.5m;水槽最宽为1.4 m,最窄为0.6 m;水槽边墙高0.5 m,边线为正弦曲线。水流方向如图2所示。试验采用美国SonTec公司的16M声学多普勒流速仪(ADV)测量三维瞬时流速,整个水槽共设37个测量断面(图3),在河宽扩展处水流比较平稳,断面间距较大,在缩窄处测量断面较密集,每个断面随槽宽的渐变设置不同数量的测量垂线。试验有两种工况:工况1流量为0.112 m3/s,下游为自由出流;工况2流量为0.100 m3/s,下游为自由出流。

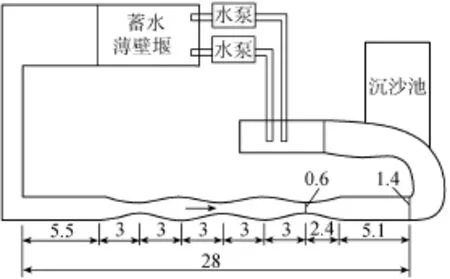
图2 渐变水槽自循环系统(单位:m)

3.3 模型验证

将工况1实测断面中轴线上的平均流速和水深测量结果分别与本文模型计算结果及SMS软件计算结果进行比较,见图4和图5(图中¯u为平均流速)。从图4和图5可以看出在进出口段,本文模型计算结果比SMS软件计算结果与实测结果吻合得更好。总体来说,平均流速和平均水深的模型计算值与实测值及SMS软件计算值较为一致。由此可知,该模型对渐变水流特性的模拟效果较好。

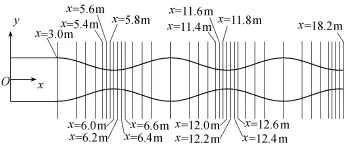
图3 试验测量断面分布

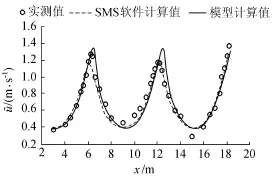
图4 实测断面中轴线沿程平均流速比较

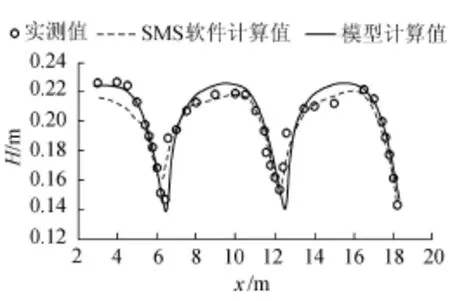
图5 实测断面中轴线沿程水深比较

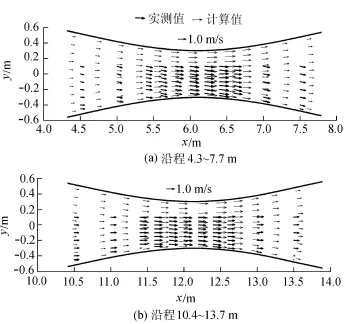
图6 缩窄断面速度场比较

图6 为典型缩窄断面速度场计算值与实测值的比较。由于所测水槽水流对称,故仅测量水槽一半宽度的流速。造成图中测量点与计算点坐标之间差异的主要原因是计算网格的疏密程度与测量断面疏密程度不一致,如果计算网格足够密,将能找到与测量断面一致的计算断面。从图中可以看出,计算速度场与实测速度场的分布规律及大小基本相同,即流速顺着边界方向变化而变化,在河宽缩窄段速度场出现收缩,流速增大;在河宽渐扩段场出现扩散,流速减小,这些现象进一步验证了模型的可靠性。

3.4 模型计算

利用数值模型模拟工况2的水流特性,计算结果与实测值的比较如图7～9所示。从图7可知,流速和水深会随着河宽变化而发生相应的变化,在最窄断面处水深最小,流速最大。从图8可以看出,工况2最窄断面处Fr最大,并且其值大于1.0,随着河道逐渐展宽,Fr逐渐减小,其值小于1.0,可见在河宽缩窄段水流处于急流状态,在河宽渐阔段水流处于缓流状态。由此可以说明,河宽的改变会影响水流的流态。从流速等值线(图9)也可以看出,在最窄断面处流速最大,但在河段最宽断面靠近边壁附近对称地出现了相对于原断面较低流速的区域,此时形成了回流区。

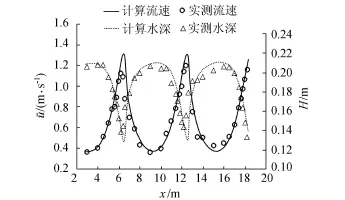
图7 断面中轴线沿程平均流速与水深

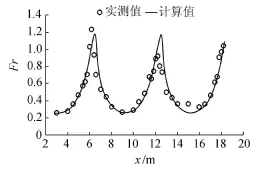
图8 Fr沿程变化曲线

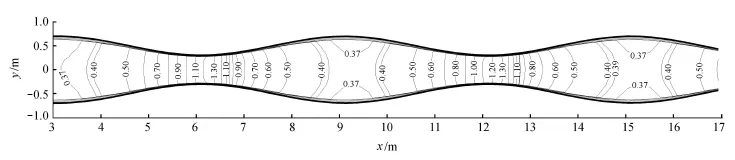
图9 流速等值线(单位:m/s)

4 结 语

针对山区河道宽窄相间的特点,采用贴体坐标法将河道不规则的边界区域转化成规则的计算区域,并利用SIMPLER计算程式求解耦合方程,基于Visual C++语言建立了山区宽窄相间河道平面二维水流数值模型。模型计算值与实测值及SMS软件计算值的比较表明:①宽窄相间河道河宽渐变将引起水深和流速的变化,在河道最窄处水深降到最低,流速最大;在河道最宽处水深达到峰值,流速最小。此外,水流运动方向随着边界的收缩和扩散将出现相应的偏移。②本文建立的平面二维水流模型对于模拟宽窄相间河道水流特性具有较高的可靠性。③该模型较好地揭示了宽窄相间河道水流流态的变化特征及其回流区特性。

[1]LUCY C,QUINE T A,NICHOLAS A.An experimental investigation of autogenic behavior during alluvial fan evolution[J].Geomorphology,2010,115(3/4):278-285.

[2]SINGHA A,BALACHANDAR R.Structure of wake of a sharp-edged bluff body in a shallow channel flow[J]. Journal of Fluids and Structures,2011,27(2):233-249.

[3]ARMELLINI A,CASARSAL,GIANNATTASIOP. Separated flow structures around a cylindrical obstacle in a narrow channel[J].Experimental Thermal and Fluid Science,2009,33(4):604-619.

[4]PAIEMENT-PARADIS G,MARQUIS G,ROY A.Effects of turbulence on the transport of individual particles as bedload inagravel-bedriver[J].EarthSurface Processes and Landforms,2011,36(1):107-116.

[5]闫旭锋,易子靖,刘同宦,等.渐变河道水流结构及局部水头损失特性分析[J].长江科学院院报,2011,28 (9):1-5.(YAN Xufeng,YI Zijing,LIU Tonghuan,et al.Flow structure and characteristics of local head loss in transition channel[J].Journal of Yangtze River Scientific Research Institute,2011,28(9):1-5.(in Chinese))

[6]ARRUDA J M,LIMA E-SILVA A L F,NETO A S,et al. Numerical simulation of channel flows using the immersed boundary method[C]//IDELSOHN S R,SONZOGNI V E,CARDONAA.South-AmericanCongresson Computational Mechanics.Santa Fe-Paraná,Argentina: [s.n.],2002.

[7]LIMAE-SILVA A F E,NETO A S,DAMASCENO J J R. Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method [J].Journal of Computational Physics,2003,189(2): 351-370.

[8]LIMAE-SILVA A F E,SILVAAR R D,NETO A S. Numerical simulation of two-dimensional complex flows around bluff bodies using the immersed boundary[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering,2007,29(4):379-387.

[9]李大鸣,陈虹,李世森.河道洪水演进的二维水流数学模型[J].天津大学学报,1998,31(4):439-446.(LI Daming,CHEN Hong,LI Shishen.A 2-D numerical model of propelling flood in the river[J].Journal of Tianjin University,1998,31(4):439-446.(in Chinese))

[10]张细兵,殷瑞兰.平面二维水流泥沙数值模拟[J].水科学进展,2002,13(6):665-669.(ZHANG Xibing,YIN Ruilan.Planar 2-Dflowandsedimentmathematical modeling[J].Advances in Water Science,2002,13(6): 665-669.(in Chinese))

[11]张大伟,程晓陶,黄金池.大坝瞬时溃决水流数值模拟:以Malpasset水库为例[J].水利水电科技进展,2009, 29(5):1-4.(ZHANG Dawei,CHENG Xiaotao,Huang Jinchi.Numerical flow modeling of instant dam failure:a case study of the Malpasset Reservoir[J].Advances in Science and Technology of Water Resources,2009,29 (5):1-4.(in Chinese))

[12]叶如意,王攀.曹娥江至宁波引水工程平面二维水流数值模拟[J].水资源保护,2010,26(5):24-28.(YE Ruyi,WANG Pan.Two-dimensional numerical simulation of flow for water diversion project from Cao'e River to Ningbo[J].Water Resources Protetion,2010,26(5):24-28.(in Chinese))

[13]方神光,黄胜伟.纯隐格式的混合有限分析法在广雅桥水流数值模拟中的应用[J].水利水电科技进展,2010, 30(6):53-57.(FANG Shenguang,HUANG Shengwei. Application of implicit schemehybridfiniteanalytic method in numerical simulation of flow effect by Guangya Bridge[J].Advances in Science and Technology of Water Resources,2010,30(6):53-57.(in Chinese))

[14]王君超.平面二维河流数值模拟方法及其应用[J].中国科教创新导刊,2010(11):93-94.(WANG Junchao.A two-dimensional numericalsimulationmethodandits application in the river[J].China Education Innovation Herald,2010(11):93-94.(in Chinese))

[15]THOMPSON J F,WARSI Z U A,WAYNE C M. Numerical grid generation:foundation and applications [M].New York:Elsevier Science Publishing Co.,1985.

[16]陈月华.干支流交汇河段水流特性计算研究[D].南京:南京水利科学研究院,2007.

[17]PATANKAR SV.Acalculationprocedurefortwodimensionalellipticsituations[J].NumericalHeat Transfer,1981,4(4):409-425.

Two-dimensional numerical simulation of flows in wide and narrow alternated channels in mountainous areas

// ZHOU Sufen1,YI Zijing1,YAN Xufeng1,YANG Qingyuan1,2,WANG Xiekang1(1.State Key Laboratory of Hydraulics and Mountain River Engineering,Sichuan University,Chengdu610065,China;2.Department of Civil and Architectural Engineering,City University of Hong Kong,Hong Kong310027,China)

The plane configuration of river channels in mountainous areas often exhibits gradual characteristics of wide and narrow alternated variations under the effect of geological conditions and riverbed evolution.A two-dimensional mathematical model for wide and narrow alternated river channels in mountainous areas was established by dividing computational domains using the body-fitted coordinates,discretizing governing equations using the finite volume method and solving equation by the SIMPLER algorithm.The model simulations were compared with the observations of flume experiment and the calculated ones by use of the hydrodynamic surface water modeling system(SMS).The results show that the proposed model can satisfactorily depict the two-dimensional flow motion characteristics of wide and narrow alternated river channels.The gradual wide variations of river channels will lead to change of their water depth and velocity. The flow velocity at the narrowest section reaches is the largest and the depth is the smallest.The flow velocity at the widest section is the smallest and the depth is the largest.

wide and narrow alternated channel;two-dimensional numerical simulation;body-fitted coordinates;finite volume method;SIMPLER algorithm

10.3880/j.issn.10067647.2013.01.005

TV131.3

A

10067647(2013)01002205

2012-03-06 编辑:骆超)

国家自然科学基金(41171016);四川大学水力学与山区河流开发保护国家重点实验室开放基金(1008)

周苏芬(1989—),女,江西新余人,硕士研究生,主要从事水力学及河流动力学研究。E-mail:512595913@qq.com

王协康(1970—),男,江西吉安人,研究员,主要从事水力学及河流动力学研究。E-mail:wangxiekang@scu.edu.cn