WASMOD水文模拟残差统计特征检验
2013-06-07李占玲徐宗学
李占玲,徐宗学,周 训
(1.中国地质大学(北京)水资源与环境学院,北京 100083;2.北京师范大学水科学研究院,北京 100875)
WASMOD水文模拟残差统计特征检验
李占玲1,徐宗学2,周 训1
(1.中国地质大学(北京)水资源与环境学院,北京 100083;2.北京师范大学水科学研究院,北京 100875)
针对采用普通最小二乘法对水文模型进行参数估计时,模型残差需满足一定的内在统计假定的要求,分别选用Levene检验、Kolmogorov-Smirnov检验和残差自相关系数图等方法对水量平衡模型WASMOD的模型残差的同方差性、正态性以及相互独立性等统计假定进行了检验。结果表明:当对原始数据未经变换而直接采用普通最小二乘法进行参数估计时,得到的模型残差满足相互独立假定,但并不满足同方差性和正态性假定;对原始流量数据进行开根号变换,可以很好地解决模型残差的异方差性和非正态性问题。在模型残差统计假定得以满足的条件下,在月时间尺度上WASMOD模型可以为莺落峡流域的流量模拟与预报提供良好的工具。
WASMOD;参数估计;普通最小二乘法;模型残差;水量平衡模型;莺落峡
由于对时间和空间尺度的依赖,无论是何种类型的水文模型都有部分参数无法通过试验直接确定,而必须借助参数估计方法来确定[1-2]。在进行水文模型参数估计时,其中一种假定是假设最优参数存在且唯一[2],此时模型参数估计问题就转化成一个最优化问题,通常采用优化方法求解,而优化方法大多都包含一些统计假定在内[3-4]。普通最小二乘法(ordinary least square,OLS)是常用的一种水文模型参数估计方法,采用该方法进行参数估计时,需假定模型残差序列相互独立且服从均值为零、方差稳定的正态分布[4]。但很少有研究对这些内在的统计假定进行检验,且已有研究表明这些假定多数情况下都得不到满足,这将意味着由此得到的最优参数并不一定最优[4-6];另外,一个模型对流域的降雨径流关系描述的成功与否通常由模型残差来表征,这进一步说明了在建模及模型应用过程中对残差的有关统计假定进行检验的必要性。本文以水量平衡模型WASMOD[7](thewater andsnowbalance modeling system,以下简称WASMOD模型)为例,选用OLS对模型进行参数估计,在此基础上探讨模型残差的一些统计特性。
1 WASMOD模型
WASMOD模型是由Xu等[7]开发的集总式概念性水量平衡模型,目前该模型已经在不同气候和土壤条件下的20多个国家的200多个流域进行了应用和验证[7],在我国黑河流域[8-9]以及南部东江流域[6]也得到了很好的应用。该模型既可以用于流量序列的外延和流域水量平衡计算,也可以用来模拟和预测气候变化条件下的水文响应及周、月尺度流量预测等。
WASMOD模型结构如图1所示。根据气温的不同,降水分为降雨和降雪。降雨作为有效降水进入到土壤含水层之前,有一部分被蒸发掉。降雪被加入到积雪层,其中有一部分降雪融化,进入土壤含水层。土壤含水层中的水分一部分蒸发,一部分形成地表径流,还有一部分形成基流。以月时间尺度为例,WASMOD模型输入数据包括研究区的月降水、月潜在蒸散发和月平均气温;输出包括径流和其他水量平衡要素,如实际蒸散发、地表径流、基流等。模型主要包括积雪、融雪、实际蒸散发、基流、地表径流、总径流和流域水量平衡等计算模块。有关该模型原理、结构及应用详见文献[7]。
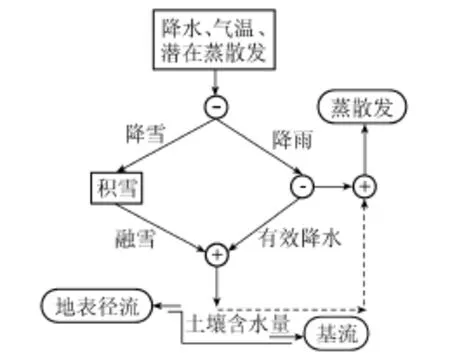
图1 WASMOD模型结构
2 研究区概况及数据资料
以黑河上游莺落峡流域为研究区。该流域面积1.0万km2,河道长303 km,河道两岸山高谷深,河床陡峻,气候阴湿寒冷,植被较好,多年平均气温不足2℃,年降水量为350 mm,是黑河流域的产流区。流域内及周边有6个雨量站(野牛沟、扎木什克、祁连、托勒、张掖、莺落峡)和4个气象站(野牛沟、祁连、托勒、张掖),站点位置如图2所示。选择流域控制站莺落峡站的流量数据率定和验证WASMOD模型,数据选用时段为1987年1月—2000年12月,其中,1987—1989年的数据作为预热期,1990—1996年的作为率定期,1997—2000年的作为验证期。数据取自中国西部环境与生态科学数据中心(http://westdc.westgis.ac.cn/)和数字黑河(http:// heihe.westgis.ac.cn/)。

图2 黑河流域及其上游莺落峡位置示意图
为准备WASMOD模型的输入数据,根据泰森多边形法,由6个雨量站月降水数据计算得到流域面月降水数据;由4个气象站的月气温数据计算得到整个流域气温数据;采用Penman-Monteith方法计算流域的潜在蒸散发[10-11]。将以上计算得到的流域面降水量、气温和潜在蒸散发数据作为WASMOD模型的输入数据。
3 模型参数估计及残差统计特征分析方法
采用OLS进行参数估计时,模型残差et需满足以下条件[4,12]:①无偏差;②方差稳定;③取值在时间上相互无关;④服从正态分布。当模型残差存在异方差时,参数的OLS估计量不再是具有最小方差的估计量;参数估计量的方差是有偏的,参数的假设检验也并非最有效,这会降低模型估计和预测的精度。当残差项存在自相关时,会夸大估计参数的显著性。因此,有必要对模型残差的同方差性、相互独立性和正态性等统计假定进行检验。
3.1 同方差性检验
采用Levene检验方法检验残差序列的同方差性[13-14]。计算Levene检验统计量F:

式中:P为样本组数;mj为第j(j=1,2,…,P)组样本数;xij为第j组第i个原始数据经数据转换后的新的变量值。Levene检验统计量F服从自由度为P-1 和N-P-1(N为各组样本数之和)的F分布。当F≥F(α,P-1,N-P+1)时,则在α=0.05或α=0.01显著性水平下拒绝H0(各组样本之间具有同方差性),接受H1,可认为各样本方差不全相等;当F<F(α,P-1,N-P+1)时,则不拒绝H0,可以认为各样本方差齐性。
3.2 正态分布检验
Kolmogorov-Smirnov(K-S)检验方法是可以用来检验单一样本是否来自某一特定分布的非参数检验方法[15-16]。设理论累积频率分布为F0(x)(这里的理论分布是正态分布),一组随机样本的经验累积频率分布为FN(x),FN(x)=k/N,其中k为样本出现的累积次数。把样本观测值从小到大排列,计算理论累积分布函数F0(x)和经验累积分布函数FN(x)。设D 为F0(x)和差距的最大值:
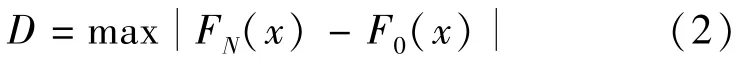
当实际观测D>D(N,α)(D(N,α)为显著性水平为α、样本数为N时,D的拒绝临界值),则拒绝H0(样本来自的总体分布服从某特定分布);反之则接受H0假设。
3.3 相互独立性检验
残差的相互独立性可以通过残差自相关系数图来判断[4,8]。残差序列et的k阶自相关系数ρk=E[(et-¯e)(et+k-¯e)]/σ2,其中,¯e和σ2为残差项的均值和方差。ρk的估计量^ρk为

当N很大而k很小时,N/(N-k)→1,则k阶自相关系数ρk的估计量为
在α=0.05显著性水平下,一个相互独立序列的自相关系数的置信区间为


4 结果分析与讨论
4.1 残差序列et的统计假定检验
定义模型残差et=Yobs,t-^Yt,其中Yobs,t为流量观测值,为流量模拟值,t=1,2,…,N。模型率定时目标函数为残差平方和最小。基于此目标函数,求出最优参数及对应的残差序列,并对此残差序列的同方差性、相互独立性和正态性进行检验。
首先将残差序列et分成3组:第1组,Yobs,t<0.9对应的残差序列,序列长度m1;第2组,0.9≤Yobs,t≤1.1对应的残差序列,序列长度m2;第3 组,Yobs,t>1.1对应的残差序列,序列长度m3。通过计算可得令,其中eij为原始残差数据,为原始残差数据中第j组(j=1,2,3)样本的算术平均。由原始残差序列生成新的序列{xij}并计算Levenes检验统计量F。计算得到F=11.18,查F分布表得到其临界值为F(0.01,2,60)=4.98,F(0.01,2, 120)=4.79。由于F=11.18>F(0.01,2,82),因此在α=0.01显著性水平下,拒绝H0,认为残差序列et不具有同方差性。
图3(a)为残差序列et的经验累积频率曲线和理论累积频率曲线以及二者差距的最大值D值,可以看出,两条累积频率曲线并不十分接近,计算得到的D=0.184>D(84,0.05)=0.148,所以拒绝H0假设,即残差序列et来自的总体分布不服从正态分布。
图4(a)为残差序列et的自相关系数图,可以看出,,即在α=0.05显著性水平下,模型残差序列et满足相互独立假设。
上述研究表明,如果定义模型残差为et=Yobs,t-,模型率定时目标函数为残差平方和最小,则得到的模型残差序列et满足相互独立但不满足同方差性和正态性假定。
4.2 残差序列ut的统计假定检验
对于方差异性的模型残差,常常需要对原始流量数据进行某种变换,如开根号变换、Box-Cox变换、取对数变换等[4-5,8]。Xu[4]研究发现,对模型验证数据做开根号变换可以很好地解决WASMOD模型残差方

图3 残差序列et和ut的经验累积频率曲线和理论累积频率曲线

图4 残差序列et和ut自相关系数

同样采用Levene检验方法对残差ut的同方差性进行检验,方法及步骤同前。计算得到对应新的残差序列ut统计量F=3.48,由于F<F(0.01,2,82),因此,可以认为在α=0.01显著性水平下,新的残差序列ut具有同方差性。
采用K-S方法检验残差序列ut来自的总体分布是否服从正态分布。图3(b)为残差序列ut的经验累积频率曲线和理论累积频率曲线以及二者差距的最大值D值,可以看出,两条累积频率曲线很接近,计算得到的D=0.082<D(84,0.05)=0.148,接受H0假设,即残差序列ut来自的总体分布服从正态分布。
通过残差自相关系数图来判断新构建的残差序列是否相互独立。图4(b)为残差序列ut的自相关系数图,可以看出,,即在0.05显著性水平下,模型残差序列ut也相互独立。
以上检验说明,变换后的残差序列满足同方差性、正态性和相互独立性等统计假定,模型参数的OLS估计量是具有最小方差的估计量,此时该模型对本研究区的流量具有良好的模拟和预测能力。
4.3 流量模拟结果
基于变换后的目标函数,得到模型参数的最优值以及模型对流量模拟的最优值。图5为流域莺落峡站实测与模拟月径流过程的对比以及流域月降水量分布,可以看出,莺落峡站的月模拟流量过程线与实测流量过程线在趋势上吻合较好。在率定和验证过程中,流量模拟的Nash-Sutcliffe有效性系数分别达到0.942和0.928,流量模拟相对误差[8]分别为-0.4%和-4.0%,在±5%以内,说明模型模拟的总体水量平衡效果较好。其中,率定期1996年、1990年、1991等年份月流量过程模拟的最好,ENS分别达到0.984、0.973和0.958,相对误差分别为-2.50%、-4.10%和3.10%;验证期中1998年效果最好,ENS达到0.943,流量模拟相对误差为-3.80%。比较未做变换时对应的流量序列模拟值,在率定期和验证期ENS分别为0.938和0.920,说明对流量数据进行变换后模型的模拟效果并没有降低。总体而言,WASMOD模型在黑河莺落峡流域的径流模拟方面具有良好的适用性,在月时间尺度上可以为研究区域的径流模拟与预报提供良好的工具。

图5 WASMOD模型对莺落峡站月流量过程模拟结果
5 结 语
OLS是较为常用的水文模型参数估计方法之一,然而以往的研究中在采用OLS进行参数估计时,往往缺乏或忽略了对模型残差需满足的一些内在统计假定进行检验。如果模型残差的这些统计假定不能满足,则由此得到的最优参数并不一定最优,导致模型的模拟和预测出现偏差。本文采用OLS对水量平衡模型WASMOD进行了参数估计,并选用Levene检验、Kolmogorov-Smirnov检验和残差自相关系数图等方法对模型残差的同方差性、正态性以及相互独立性等统计假定进行了检验。结果表明,当对原始数据未经任何变换而直接采用OLS进行参数估计时,得到的模型残差满足相互独立假定,但并不满足同方差性和正态性假定;当把原始数据进行开根号变换时,得到的残差序列满足同方差性和正态性假定。在此统计假定得以满足的条件下,对黑河上游莺落峡流域的流量进行了模拟,结果表明,在月时间尺度上WASMOD模型可以很好地模拟莺落峡流域的流量过程。
[1]REFSGAARD J C,SETH S M,BATHURST J C,et al. Application of the SHE to catchments in India:partⅠ: general results[J].Journal of Hydrology,1992,140:1-23.
[2]王书功.水文模型参数估计方法及参数估计不确定性研究[D].北京:中国科学院研究生院,2006.
[3]WANG Y,DIETRICH J,VOSS F,et al.Identifying and reducing model structure uncertainty based on analysis of parameter interaction[J].Advances in Geosciences,2007, 11:117-122.
[4]XU Chongyu.Statistical analysis of parameters and residuals of a conceptual water balance model-methodology and case study[J].Water Resources Management,2001,15:75-92.
[5]YANG Jing,REICHERT P,ABBASPOUR K C,et al. Hydrological modelling of the Chaohe Basin in China: statistical model formulation and Bayesian inference[J]. Journal of Hydrology,2007,340:167-182.
[6]LI Lu,XU Chongyu,XIA Jun,et al.Uncertainty estimates by Bayesian method with likelihood of AR(1)plus normal model and AR(1)plus multi-normal model in different time-scales hydrological models[J].Journal of Hydrology, 2011,406:54-65.
[7]XU Chongyu.WASMOD:the water and snow balance modelling system[M]//SINGH V P,FREVERT D K. Mathematical Models of Small Watershed Hydrology and Applications:Chapter 17.Chelsea,Michigan,USA:Water Resources Publications,LLC,2002:555-590.
[8]LI Zhanling,XU Zongxue,LI Zhanjie.Performance of WASMOD andSWATonhydrologicalsimulationin YingluoxiawatershedinnorthwestofChina[J]. Hydrological Processes,2011,25:2001-2008.
[9]李占玲,徐宗学.黑河流域上游山区径流模拟及模型评估[J].北京师范大学学报:自然科学版,2010,46(3): 344-349.(LIZhanling,XUZongxue.Assessmenton hydrological models for runoff simulation in the upper reaches of the Heihe River Basin[J].Jonrnal of Beijing Normal University:Natural Science,2010,46(3):344-349.(in Chinese))
[10]MONTEITH JL.Evaporation,theenvironment[C]// XIXth symposia of the society for Experimental Biology in the State and Movement of Water in Living Organisms. Cambridge:Cambridge University Press,1965:205-234.
[11]左德鹏,徐宗学,程磊,等.渭河流域潜在蒸散量时空变化及其突变特征[J].资源科学,2011,33(5):975-982. (ZUO Depeng,XU Zongxue,CHENG Lei,et al.Spatialtemporalvariationsandmutationsofpotential evapotranspirationintheWeiheRiverBasin[J]. Resources Science,2011,33(5):975-982.(in Chinese))
[12]单明,聂燕萍.最小二乘法直线拟合基本假定的几点讨论[J].大学物理实验,2008,21(4):63-65.(SHAN Ming,NIE Yanping.Discussion on assumptions of least square linear fitting[J].Physical Experiment of College, 2008,21(4):63-65.(in Chinese))
[13]龚秀芳,冯珍珍.几种异方差检验方法的比较[J].菏泽师范专科学校学报,2003,25(4):19-23.(GONG Xiufang,FENGZhenzhen.Comparingseveraltesting methodsofheteroscedasticity[J].JournalofHeze Teachers College,2003,25(4):19-23.(in Chinese))
[14]郭显光.方差齐次性检验的方法[J].统计教育,2005 (4):32-33.(GUOXianguang.Testingmethodsfor homoscedasticity[J].Statistical Education,2005(4):32-33.(in Chinese))
[15]褚健婷,夏军,许崇育,等.海河流域气象和水文降水资料对比分析及时空变异[J].地理学报,2009,64(9): 1083-1092.(CHU Jianting,XIA Jun,XU Chongyu,et al. Comparisonandspatial-temporalvariabilityofdaily precipitation data of weather stations and rain gauges in Haihe River Basin[J].Acta Geographica Sinica,2009,64 (9):1083-1092.(in Chinese))
[16]孙鹏,张强,陈晓宏.鄱阳湖流域枯水径流演变特征、成因与影响[J].地理研究,2011,30(9):1702-1712. (SUN Peng,ZHANG Qiang,CHEN Xiaohong.Changing propertiesoflowstreamflow:possiblecausesand implications[J].Geographical Research,2011,30(9): 1702-1712.(in Chinese))
[17]NASH J E,SUTCLIFFE J V.River flow forecasting through conceptual models:partⅠ:a discussion of principles[J].Journal of Hydrology,1970,10,282-290.
[18]张利平,曾思栋,王任超,等.气候变化对滦河流域水文循环的影响及模拟[J].资源科学,2011,33(5):966-974.(ZHANG Liping,ZENG Sidong,WANG Renchao,et al.Impacts of climate change on the hydrological cycle in the Luan River Basin[J].Resources Science,2011,33 (5):966-974.(in Chinese))
Check of statistical features of model residuals of WASMOD
//LI Zhanling1,XU Zongxue2,ZHOU Xun1(1.College of Water Resources and Environment,China University of Geosciences,Beijing100083;China;2.College of Water Sciences,Beijing Normal University,Beijing100875,China)
When the parameters for hydrological models are estimated by using the ordinary least square method,the model residuals should satisfy certain statistical assumptions.The Levene test,Kolmogorov-Smirnov test and autocorrelation coefficient are employed to check the statistical assumptions of model residuals of the conceptual lumped Water And Snow balance MODeling system(WASMOD)such as homoscedasticity,normality and independence features.As the original discharge values without any transformation are calculated by using the ordinary least square method,the yielded model residuals are proved to be independent,which greatly deviate from the features of homoscedasticity and normality. However,a square root transformation for the discharge values is capable of solving the problems of heteroscedasticity and non-normality in model residuals.The proposed WASMOD model may be satisfactory tool for the simulation and predication of discharge in Yingluoxia watershed on monthly temporal scale when the statistical assumptions of the model residuals are satisfied.
WASMOD;parameter estimation;ordinary least square method;model residual;water balance model; Yingluoxia watershed
10.3880/j.issn.10067647.2013.01.003
P333.6
A
10067647(2013)01001305
2012-04-26 编辑:熊水斌)
国家自然科学基金(41101038);中央高校基本科研业务费专项(2011YXL038)
李占玲(1980—),女,内蒙古赤峰人,讲师,博士,主要从事水文及水资源研究。E-mail:zhanling.li@cugb.edu.cn
