水电站励磁系统参数优化研究

刁晓虹，夏潮

（中国电力科学研究院，北京市 100192）

0 引 言

西部某水电站装机容量3600MW，安装6台单机容量600MW的混流式水轮发电机组，是国家“十五”重点建设项目［1－2］。由于电网建设与电源建设、负荷发展存在时间差，现有网架结构和地区用电负荷难以满足该水电送出的需求；水电送出需求和地区用电需求难以充分满足。其次，该电网区外特高压线路、区外部分重要输电断面的潮流及方向以及区外电网的阻尼特性显著地影响该电网的稳定水平，从而对该电网交流外送通道及区域内主要水电送出通道的送电能力构成压力，限制了水电站的送电能力。2009年底，电网稳定计算结果表明：该水电站只要有1台机组额定负荷运行，在该区域某断面N－1故障时，系统就会失去动态稳定。系统的动态稳定性问题可以通过优化并网机组的电力系统稳定器（power system stabilization，PSS）参数来得到改善。本文在综合考虑系统需求及机组稳定性的基础上，首先确定PSS参数优化方案，然后对该电站5、6号机组进行PSS参数优化后现场试验验证工作［3］，最后对PSS参数优化后该水电站的送出能力进行计算，和原始参数下水电站的送出能力进行比较，以证明PSS参数优化方案的有效性和可行性［4］。

1 励磁系统原始参数及原始参数下水电站的送出能力

1.1 励磁系统原始参数

水电站G1、G3、G5采用通用电气加拿大公司生产的600MW水轮机，G2、G4、G6采用东方电机有限公司生产的600MW水轮机。G1G6发电机均采用东方电机有限公司的600MW水轮发电机，励磁系统采用自并励励磁系统，励磁调节器为ABB公司的UNITROL 5000型微机励磁调节器，该励磁调节器是双通道励磁调节器，励磁调节器控制方式采用的是比例积分微分（proportional integral derivative，PID）＋PSS控制。PID环节的数学模型如图1所示，PSS可使用4型PSS，传递函数如图2所示。图1中：Ut为发电机机端电压；TR为电压采样环节时间常数；Uref为参考电压；UPSS为PSS输出；UP＋为 AVR 输出上限；UEF为调节器输出电压；UP－为AVR输出下限；KR为增益；TC1、TC2、TB1、TB2为超前、滞后环节时间常数。图2中：ω0、PG0为角速度和功率参考值；ωG、PG分别为发电机角速度和功率；Trw为角速度控制时间常数；Kr为功率控制增益；Trp为功率控制时间常数；TW为惯性环节系数；TW1、TW2、T5、T6、T7为隔直环节时间常数；T9、T10、T12为高频滤波环节时间常数；T1、T2、T3、T4、T13、T14为超前、滞后环节时间常数；KP为增益；Usmax、Usmin为PSS最大、最小输出。

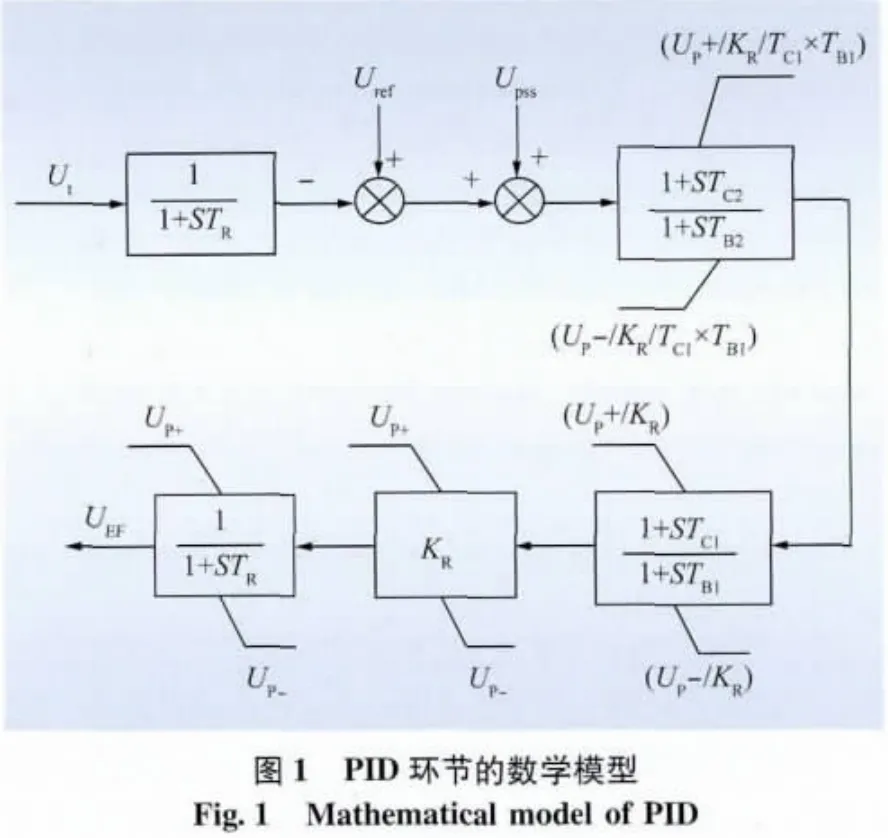
图2中，PSS的原始参数为：T5＝T6＝T7＝5s；Trw＝0.02s；T9＝0.6s；T10＝T12＝0.12s；Kp＝3；Kr＝0.15；Tw＝0.54s；Tw1＝5s；Trp＝0.02s；Tw2＝5 s；T1＝0.25s；T2＝0.04s；T13＝T14＝0.1s；T3＝0.3s；T4＝0.03s；Usmax＝0.1pu；Usmin＝－0.1pu。

1.2 原始参数下水电站的送出能力

电力系统动态稳定性的研究方法包括频域法［5－9］和时域法［7－9］，本项目在计算研究工作中以频域法为主，并用时域法加以校验。通过时域法和频域法对水电站机组PSS阻尼效果进行评估，对比小干扰及大干扰稳定计算时的阻尼比。其中大干扰暂态计算只对省间某双回联络线进行了三相短路N－1故障的校验，故障点设置在500kV母线2%的位置，故障时间100ms。小干扰稳定计算结果见表1。

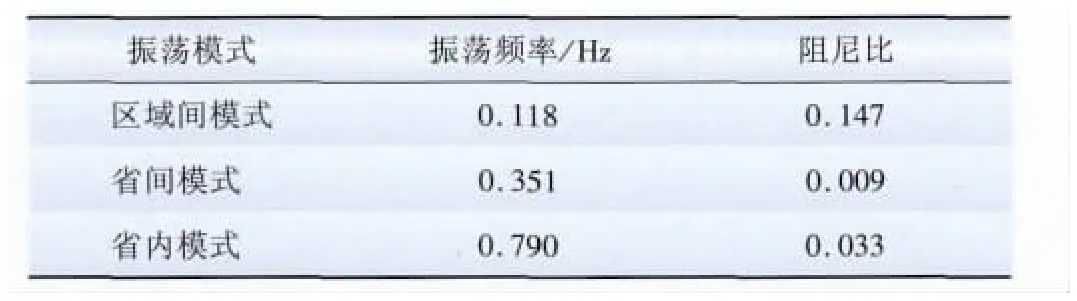
表1 小干扰稳定计算结果Tab.1 Calculation results of small signal stability

联络线三相短路N－1暂态稳定计算结果见图3，大干扰阻尼比为－0.329。

图3 水电站6号机与三峡左岸1号机相对功角Fig.3 Opposite power angle of No.6generator in hydropower station and No.1generator in Three Gorges Left Bank Station

仿真结果表明：考虑水电站自带旋转备用，直流外送通道外送300MW时，水电站及相邻电站最大输出电力为1765MW，直流外送通道不外送时最大输出电力为1365MW。

2 励磁系统参数优化方案

2.1 PSS针对主要振荡模式进行重点补偿

按丰水期该电站4台机和相邻电站1台机的开机方式研究系统的动态稳定水平，通过对该电网进行小干扰稳定分析，针对系统存在的与水电站强相关的振荡频率约0.33Hz的振荡模式进行研究。

2.2 提高PSS临界增益

对电站励磁系统PSS模型参数进行优化研究，以提高PSS临界增益进而提高机组运行增益。优化后PSS的参数有更平缓的幅频特性，有效地降低了PSS高频段的幅值，可以提高PSS的临界增益。

2.3 PSS改用2B模型

此次优化没有对PID参数做出调整，因此励磁系统无补偿特性仍采用原始数据，PSS模型在原有PSS2A模型上增加一级超前滞后环节，改造为PSS2B模型［10］。使用多目标鲁棒参数优化专用仿真软件对该电站PSS参数进行优化。优化后5、6号机的PSS参数为：TW1＝TW2＝TW3＝T7＝5s；TW4＝0s；T1＝0.1s；T2＝0.06s；T3＝0.5s；T4＝0.12s；T10＝0.2s；T11＝0.07s；T8＝0.6s；T9＝0.12s；M＝5；N＝1。参数优化后的PSS较大幅度地降低引起发电机励磁闭环系统电磁振荡的因素，提高增益。

2.4 阻尼效果校核

分别在现场发电机带约50%负荷和100%负荷时进行优化试验研究，进行优化参数后的PSS效果检验。

3 PSS参数优化后的仿真计算及现场试验

3.1 有补偿励磁系统频率响应特性仿真

根据PSS模型和仿真计算得到5、6号机PSS环节的频率特性“φe”和励磁系统的有补偿特性“φe＋φpss”，计算结果如图4所示。

图4 相频特性Fig.4 Phase－Frequency characteristics

由图4可见，在0.12.0Hz的频率范围内，由PSS产生的电磁力矩的阻尼分量为正（在0.1Hz附近，PSS2B模型参数比原始参数相位补偿效果略有下降），PSS对地区振荡频率和联网系统振荡频率都具有较好的阻尼，PSS相位补偿可以满足要求。

3.2 PSS增益调整试验

理论上讲，在正确的相位补偿下，PSS的增益越大，其提供的正阻尼越强，但实际上，电力系统是一个高阶的复杂系统，增加PSS的增益虽然可以增加某些机电振荡的阻尼，但如果PSS增益过大，也可能引起PSS调节环振荡，使系统出现不稳定，此时，发电机的励磁电压和无功功率可能出现明显摆动甚至是等幅或增幅摆动，因此，PSS实际存在一个能稳定运行的最大增益，即临界增益。PSS的运行增益一般取临界增益的1／51／3，以留有足够的增益裕度，水电站的运行增益取临界增益的1／2，增益裕度略低于这个水平。这主要是考虑到2个因素：（1）系统动态稳定的需要；（2）运行增益KS1为15时，励磁闭环系统运行正常，发电机未出现无功波动现象，励磁电压稳定。5、6号机的PSS运行增益Ks1为15时，录波图见图5。

图5 取Ks1＝15时的录波图Fig.5 Recorded diagram as Ks1＝15

图中：UAB为发电机机端线电压；P为发电机有功功率；Q为发电机无功功率；UFD为发电机励磁电压；IFD为发电机励磁电流。

3.3 PSS阻尼效果校核试验

发电机并网运行，先将PSS切除，进行2%的电压阶跃试验，同时启动WFLC录波，记录有功功率的摆动幅值和次数。将PSS投入，同样工况下重复以上试验，记录和观察2次的录波图，PSS投入运行时，有功功率的摆动幅值和次数应减少。

图6为水电站5、6号机PSS退出和投入2种情况下的电压阶跃试验录波图。由图6可以看出，PSS对于发电机组机的本机振荡有明显的抑制作用。

图6 机端电压2%阶跃时的录波图Fig.6 Recorded diagram as 2%step of generator voltage

3.4 反调试验

PSS的原理是通过励磁系统的作用抑制有功功率的低频振荡，可以说PSS是通过无功功率的波动来抑制有功功率的波动，所以，在正常情况下，投入PSS后较不投PSS时无功功率的波动要大一些，只要无功功率的波动在合适的范围内，就可认为正常。另外，用电功率作为输入信号的PSS在原动机功率发生变化时，由于PSS自己不能区分系统波动和原动机功率波动，仍然作用于励磁系统，造成无功功率波动，这种现象就叫“反调”［11－13］，如果反调的影响太大，就需要在执行增减有功功率操作时闭锁PSS的作用。PSS采用IEEE－2B模型从原理上讲，是不会有“反调”的。

5、6号机组反调试验结果如图7所示。5号机组PSS无功反调试验时，有功功率从344MW下降到290MW，再从290MW上升到344MW，无功反调现象不明显。6号机PSS无功反调试验时，有功功率从344MW下降到320MW，再从320MW上升到344MW，无功反调现象不明显。

图7 PSS反调试验Fig.7 Reverse action test of PSS

4 PSS参数优化后水电站的送出能力

4.1 水电站送出1台机

用电力系统综合分析程序（PSASP）对水电站PSS参数优化前后电网的稳定性进行分析［8］，小干扰稳定计算结果为：优化前，振荡频率0.351Hz，阻尼比0.009，为弱阻尼；优化后，振荡频率0.348Hz，阻尼比0.040，为中等阻尼。

联络线三相短路N－1暂态稳定计算结果见图8。

4.2 水电站送出4台机

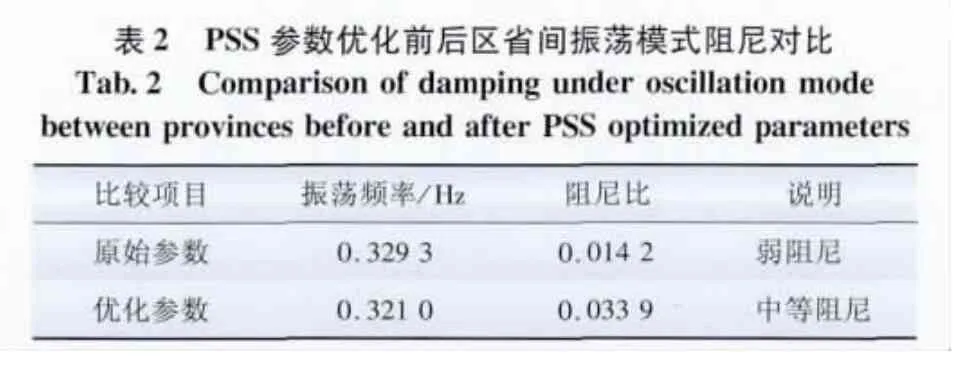
水电站开机方式选择为4台机组，相邻水电站开机方式为1台。故障设置为500kV双回联络线一回线路靠近一端500kV母线侧三相短路接地，线路跳闸。表2给出了优化前和优化后的暂态稳定计算结果。从暂态稳定计算结果看，优化后省间振荡模式的大扰动阻尼比明显提高。

?

图9为水电站机组相对于三峡水电站机组的相对功角曲线，优化前在系统最严重的N－1故障下，系统动态稳定失稳。优化后参数在系统最严重的N－1故障下，系统没有失去稳定。

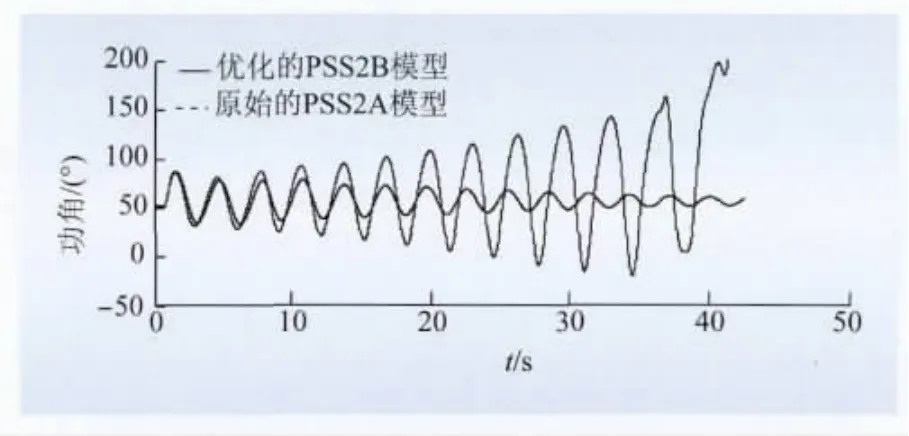
图9 水电站6号机对于三峡电站左1号机的相对功角曲线Fig.9 Opposite power angle of No.6generator in hydropower station and No.1generator in Three Gorges Left Bank Station

4.3 考虑旋转备用

仿真计算结果表明：采用优化的PSS2B模型，考虑水电站自带旋转备用，直流外送通道外送300MW时，水电站和相邻电站最大输出电力为2900MW，直流外送通道不外送时最大2700MW，分别比原始参数提高输送能力31.4%和26.7%。

5 结 论

（1）水电站投运初期，机组并网满发时，系统中存在1个阻尼很弱的省间振荡模式，该模式与该水电站送出能力强相关，严重威胁区域电网的安全。计算结果表明即使水电站自带旋转备用，水电站和相邻电站最大输送电力仅为1765MW，仅为2电站总装机容量的41%。水电站机组投产初期，该振荡模式频率为0.351Hz，阻尼比为0.009的弱阻尼模式，这是限制水电站5、6号机组电力送出的主要原因。（2）对PSS参数优化，是提高系统阻尼最有效、最经济快捷的手段。PSS参数优化方案为提高PSS的临界增益，将PSS模型由原有的PSS2A模型改造为PSS2B模型，增加1级超前滞后环节。参数优化后的PSS高频段幅值降低，减轻引起发电机励磁闭环系统电磁振荡的因素，提高了运行增益。（3）通过现场试验以及2010年典型方式计算结果验证了优化方案的有效性和可行性，确定了PSS优化参数。（4）优化后的参数提高了该电网夏季丰水期电网的系统阻尼，保证了水电站满负荷运行4台机组和相邻电站满负荷运行1台机组方式下该电网的动态稳定性，可以将该水电站和相邻电站开机极限功率由1765MW提高到2900MW，达到总装机容量的68.1%，提高量为总装机容量的31.4%。

［1］夏潮，郭文波，沈成平.国电大渡河瀑布沟水电站励磁系统参数优化研究［R］.北京：中国电力科学研究院，2010.

［2］夏潮，郭文波，沈成平.四川电网现有结构下系统动态稳定性对瀑布沟和深溪沟电站电能消纳能力影响分析及应对策略研究［R］.北京：中国电力科学研究院，2010.

［3］李基成.现代同步发电机励磁系统设计及应用［M］.北京：中国电力出版社，2009：76－82.

［4］中国电力科学研究院.电力系统分析综合程序说明书［R］.北京：中国电力科学研究院，2004.

［5］刘取.电力系统稳定性及发电机励磁控制［M］.北京：中国电力出版社，2007：306－310.

［6］黄顺礼.抑制机组振荡用国际典型电力系统稳定器［J］.电力建设，2002，23（9）：38－41.

［7］竺士章.发电机励磁系统试验［M］.北京：中国电力出版社，2008：124－145.

［8］Kundur P.电力系统稳定与控制［M］.北京：中国电力出版社，2002：766.

［9］李文锋，李莹，吴琛.云南电网励磁系统参数评估与PSS参数优化研究［R］.北京：中国电力科学研究院，2009.

［10］韩石成.小浪底水电厂电力系统稳定器无功反调现象及分析［J］.水电能源科学，2007，25（2）：116－118.

［11］杨立强，王亮，赵红光，等.加速型电力系统稳定器的研制［J］.电网技术，2004，28（23）：57－60，80.