关注学生的认知基础 注重知识的形成过程——有感于《折线统计图》一课的教学

■ 王 钊

关注学生的认知基础 注重知识的形成过程
——有感于《折线统计图》一课的教学

■ 王 钊

在武汉市“课内比教学”的活动中，作为我区数学中段（三、四年级）的参赛选手——武汉市育才二小的高巍娟老师，抽到的教学内容是义务教育课程标准实验教科书四年级下册第7单元《统计》的第一课时。这节课的教学目标是通过对数据的简单分析，使学生进一步体会统计在生活中的意义和作用，认识单式折线统计图，了解折线统计图的特点，会看折线统计图，并能根据统计图回答简单的问题。

在此之前，学生已经具备了一定的收集数据、整理数据的能力，认识了统计表和条形统计图，会根据统计图表发现问题并解决问题。

基于学生已具备的认知基础和生活经验，我们创设了学生熟悉的科技馆机器人表演的情境，从一名学生的“数学日记”中提炼数学信息，从而整理出数据，绘制条形统计图，很好的与新知接轨。

认识折线统计图，我们更加关注知识的形成过程：从认识横轴、纵轴表示的意义、到形成格子图；从描点、连线、标数、到形成折线，在折线统计图的形成过程中，学生对折线统计图的特点（不仅能反映数量的多少，还能清晰地看出数量的增减变化）的了解就水到渠成了。

下面，我就借助以下两个教学片段具体诠释：

【教学片段】

片段一：源自情境，勾连旧知

师：大家看，这是什么场景？

（播放武汉市科技馆机器人演奏会的视频。）

生1：机器人演奏会。

生2：我看过，是科技馆的机器人演奏会。

师：随着科学技术的发展，科技馆里高科技的表演也越来越多了，我们班的刘宇浩同学看了这个表演后，写了一篇非常精彩的数学日记。我们一起来看看！（展示学生的数学日记）

师：现在老师想知道1998～2003年每年中小学参观科技馆的人数，你能立刻告诉我吗？

生3：有点困难，要找一下。

生4：还没有想好。

师：那能用我们学过的知识来解决这个问题吗？

生5：可以先从日记中整理出数据，再用统计表表示。

生6：还可以用条形统计图绘制出来，这样就能看得很清楚了。

师：你们所说的都是“统计”的知识。（板书单元课题——统计）统计是我们的老朋友了，想知道1998～2003年每年参观科技馆的人数，我们可以先整理出数据，绘制成统计表和条形统计图。

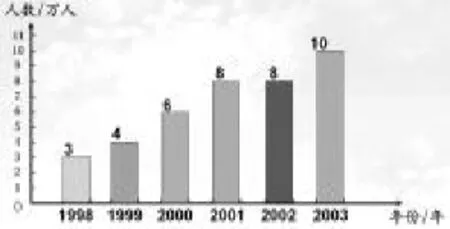
XX市中小学生参观科技展人数统计图（1998-2003年）

师：看一看，从中你获得那些信息呢？

（学生回答略）

师：我们已经知道，条形统计图能让我们清楚的看出数量的多少。

片段二：关注过程，促进认识

1.格子图的形成

师：你们知道吗？统计图还可以这样画。

XX市中小学生参观科技展人数统计图（1998-2003年）

XX市中小学生参观科技展人数统计图（1998-2003年）

XX市中小学生参观科技展人数统计图（1998-2003年）

XX市中小学生参观科技展人数统计图（1998-2003年）

师：请大家观察，什么没有变？

生1：它的标题、横轴和纵轴没有变。

师：那横轴和纵轴分别表示的是什么？

生2：横轴表示1998年到2003年的年份。

生3：纵轴表示人数，单位是万人。（举例说明每条横线和竖线对应的含义）

师：有了这样的横线和竖线，一张格子图就形成了。看看接下来出现了什么？

2.点和折线的形成

XX市中小学生参观科技展人数统计图（1998-2003年）

XX市中小学生参观科技展人数统计图（1998-2003年）

XX市中小学生参观科技展人数统计图（1998-2003年）

生4：原来的直条变成了一个个点。

师：看这个点（指着第一个点），你知道它表示什么意义吗？

生5：它纵向对应年份，横向对应人数。

生6：对！第一个点表示1998年参观科技馆的人数有3万人。

师：说得太好了！你们能像这样说说其余几个点表示的具体含义吗？

（学生踊跃发言，逐个说清每个点表示的含义。）

师：接下来，这些点要“手拉手”连起来了。这样一条条线段连接起来，形成了一条折线。

3.折线统计图的形成

师：这样一幅新的统计图就形成了。你们知道这样统计图叫什么吗？

生7：折线统计图！师：看来你真是见多识广！(板书：折线统计图)下面，我们一起来认识它。

【案例评析】

《折线统计图》属于“统计与概率”领域的内容，旨在增强学生的统计意识，提高统计素养，能运用统计知识解决简单的数学问题。这节课的内容难度不大，而且与生活实际密切联系，学生学习起来基本能达到教学目标。但教学中始终感觉有些缺憾：我们更多地关注到成型后的折线统计图的识图，而忽视了它的各个部分：横轴、纵轴、点、线、数的形成过程及含义；我们更多地关注到折线统计图与条形统计图特点的结论语，而忽视了对折线统计图特点的体验和提炼过程。基于此，我们对本节课的教学设计进行了再修改。

一、关注学生的认知基础，经历统计的全过程

美国心理学家奥苏伯尔认为，当学习新的知识时，如果在学生原有知识结构中，能找到适当的可以用于同化新知识的原有知识，那么该学生的认知结构就具有原有知识的可利用性。他认为，原有知识的可利用性是是影响新的学习和迁移的最重要因素，也是最重要的认知结构变量。在学习折线统计图之前，学生会进行简单的数据收集与整理，会完成统计表和条形统计图的制作，并会根据统计图表解决问题。基于学生已具备的认知基础和生活经验，我们创设了学生熟悉的科技馆机器人表演的情境，从一名学生的“数学日记”中展开，通过老师的一句精妙的提问“现在我想知道1998～2003年每年中小学参观科技馆的人数，你能立刻告诉我吗？”这个问题驱使着学生摒弃其它无关因素，从日记中提炼数学信息，对数据进行整理加工，实际上就是运用统计的知识来解决这个问题。使我不由得想起古希腊学者普罗塔戈说过的一句话：头脑不是一个需要被填满的容器，而是一把需要被点燃的火把，而点燃这个火把的火星就是教师的提问。然后学生根据整理出的数据，绘制条形统计图，很好地与新知接轨，为认识折线统计图奠定坚实的基础。

二、关注知识的形成过程，了解折线统计图的特点

最初的设计，我们在条形统计图的基础上直接端出折线统计图，让学生观察后概括其特点。这样的设计虽然也能基本实现教学目标，但是学生在理解条形统计图及折线统计图的内在联系与各自特点上还是存在盲点。为什么条形统计图能清楚地反映数量的多少？而折线统计图不仅能反映数量的多少，还能清楚地看出数量的变化情况？这是由于这两种统计图自身的表现形式决定的：条形统计图是通过直条的高低来表示数量的多少；折线统计图一方面通过点的高低位置显示数量的多少，另一方面又通过折线的平缓和陡峭来折射数量的变化情况。因此，识图的过程中，我们将折线统计图的形成过程一步步展示在学生面前：在条形统计图的基础上，逐渐淡化直条，保留横轴和纵轴。从认识横轴、纵轴表示的意义、到形成格子图；从描点、连线、标数、到形成折线，在折线统计图的形成过程中，学生对折线统计图的特点的了解就水到渠成了。

现在，很多教师追求课堂的开放和多样化，我觉得这并不意味着可以随心所欲。教师必须遵循学生的认知规律和课堂教学的基本规律，所谓千变万变，万变不离其宗。关注学生的认知基础，注重知识的形成过程，这样的课堂一定是学生向往的课堂！

（作者单位：武汉市江岸区小学教研室）

责任编辑向保秀