基于复影响系数的载重轮胎动平衡机标定算法
2013-06-05刘迎澍尹建华巫上清
刘迎澍,尹建华,巫上清
基于复影响系数的载重轮胎动平衡机标定算法
刘迎澍1,尹建华1,巫上清2
(1. 天津大学电气与自动化工程学院,天津 300072;2. 中兴通讯股份有限公司微电子研究院,深圳 518052)
动平衡是检测轮胎质量的重要技术指标.研究了载重轮胎动平衡检测设备的核心技术,即系统参数标定算法.针对轮胎-轮辋-主轴动力学系统的复影响系数方程,提出了基于最小二乘的标定算法来解算影响系数.验证实验中在轮辋上安装砝码,来检测参数标定精度,其质量计算误差在±1%的范围内.与传统的参数标定方法相比,本算法能够更有效地消除系统误差的影响,求解得出的影响系数方程能够更准确地表征轮胎不平衡质量与主轴支承振动信号间的对应关系.
动平衡机;参数标定;复影响系数
动平衡是评价轮胎质量的重要技术指标,轮胎动平衡性能的优劣将直接影响到车辆行驶的舒适性、稳定性和安全性.我国是轮胎制造大国,各类轮胎产品的产量及出口量居世界前列,但是在高精度检测设备方面长期依赖进口.近年来,我国在轮胎动平衡检测设备的研发和制造领域取得了长足进步,相继推出了一系列具有自主知识产权的研究成果[1-7],改变了国内轮胎制造企业单纯依赖进口检测设备的状况.但是,在大型轮胎(如载重轮胎、工程轮胎等)检测设备的总体设计、核心算法等关键技术方面还有待提高,这也是我国轮胎检测装备制造业当前所面临的一个严峻挑战.
大型轮胎动平衡检测设备结构复杂,长时间处于高负荷运行状态,与之相关的诸多复杂因素所造成的系统误差对于检测的精度和一致性具有很大影响.参数标定算法是动平衡检测系统的核心技术,因为轮胎的不平衡量是通过测量动平衡机主轴支承振动的方法间接得到的,需要通过参数标定来解算不平衡量与振动信号之间的关系.影响系数法是转子动平衡领域最常用的建模方法,其特点是将整个测量系统的内部结构看作一个黑箱,仅通过影响系数来表征转子不平衡量与支承振动之间的线性耦合关系,因此无需复杂的系统建模.
该方法广泛应用于高速主轴自动平衡装置[8]、中小型电机转子动平衡校正[9-10]、盘状零件数控加工过程的主轴减振[11]等领域.文献[12]还通过查询转子在不同转速下的影响系数表来计算电磁平衡器的控制量,以实现减振效果.影响系数的计算方法有多种:文献[13]用凸优化方法来解算柔性转子的影响系数方程;文献[14]用自适应参数估计法求解汽车起动电机的影响系数方程;文献[15]将贝叶斯法用于影响系数的在线估计.
对于动平衡检测设备的影响参数标定来说,传统的影响系数求解过程是通过解析解直接得到的,如文献[5]所采用的复影响系数求解法.这种方法不能适应因设备运行环境、部件磨损等多方面原因所引起的系统模型变化,因此在实际运行中计算精度会受到一定影响.文献[6-7]研究了基于最小二乘和实影响系数方程的多传感器标定算法,求解精度优于直接求解法,但由于省略了影响系数中的相位信息,因而对支承系统阻尼引起的相移无补偿能力.针对上述问题,笔者建立了轮胎不平衡量与主轴支承振动信号之间的复影响系数方程,研究了基于最小二乘的求解算法,从而使影响系数的计算精度得到进一步提高.
1 轮胎动平衡检测系统
载重轮胎动平衡检测设备如图1所示,检测系统的构成如图2所示.

图1 载重轮胎动平衡检测装置Fig.1 Tire dynamic balance testing machine
动平衡机的参数标定过程包括以下步骤:①通过闭环伺服驱动系统(由主轴伺服电机、伺服驱动器、工控机、高速计数卡、I/O接口卡以及与主轴同轴安装的高精度旋转编码器构成),使主轴的转速保持在400,r/min,转速波动被控制在±0.2%范围内;②对压电传感器(经电荷放大器)输出的主轴振动信号进行同步采样和频谱分析,高阶FIR滤波和高精度FFT算法有效保障了振动信号的幅值和相位的计算精度;③采用最小二乘影响系数法进行参数标定实验.

图2 轮胎动平衡检测系统Fig.2 Block diagram of tire dynamic balance testing system
2 轮胎-轮辋-主轴系统影响系数方程
由于轮辋的加工精度非常高,与被测轮胎相比,其不平衡量可忽略不计.因此可将充气后的轮胎和轮辋看作一个整体,以简化系统模型.根据刚性转子的两面平衡原理,轮胎自身的不平衡量可等效为其两个胎侧面(即刚性转子的两个校正面)上的不平衡量.
轮胎-轮辋-主轴系统受力情况如图3所示,各变量定义为
Mu、Ml分别为上、下校正面上的不平衡量;
φu、φl分别为上、下不平衡量的相位角;
Fu、Fl分别为上、下不平衡量产生的离心力;
Uu、Ul分别为上、下支承传感器的测量信号.
传感器的测量信号与轮胎不平衡量之间关系可表示为

式中k1、k2、k3、k4就是测量系统的影响系数,是受诸多复杂因素影响的特征矢量.将k1、k2、k3、k4、Mu、Ml、Uu、Ul分解成虚部与实部,即
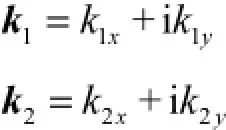

式中的k1x、k2x、k3x、k4x、k1y、k2y、k3y、k4y就是需要标定的参数.

图3 轮胎-轮辋-主轴系统动力学模型Fig.3 Model of tire-rime-spindle dynamics
3 基于最小二乘的参数标定算法
3.1 用于参数标定的数据采集
1) 不加砝码测量
为计算影响系数,需要采集3组数据.首先在上、下轮辋均未安装校正砝码时采集传感器的振动信号,影响系数方程如式(1)所示.
设Uu和Ul的离散信号序列分别为Uui(i=0,1,…,N-1)和Uli(i=0,1,…,N-1),其中N为采样点数.计算出Uu和Ul的幅值Uu、Ul和初相位φu0、φl0,再求出Uui和Uli所在x、y轴的分量Uuxi、Uuyi、Ulxi和Ulyi(i=0,1,…,N-1).
2) 上轮辋安装砝码
在上轮辋0°位置加装质量为m0的校正砝码,设上、下传感器的输出分别为Uˆu和Uˆl,则影响系数方程为

由式(2)-式(1)得到

计算出Uˆu和Uˆl的离散序列在x轴和y轴的分量Uˆuxi、Uˆuyi、Uˆlxi和Uˆlyi(i=0,1,…,N-1),设N0为主轴每转一周的采样点数,则对应的离散方程为

式中

3) 下轮辋安装砝码
在下轮辋0°位置安装质量为m0的砝码,设上、下传感器的信号为uU˜和lU˜,因而有

由式(8)-式(1)得到
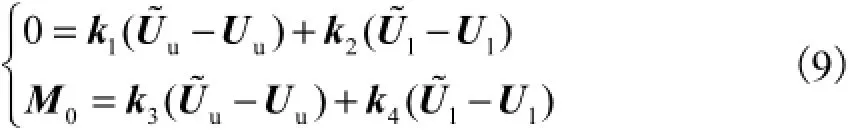
计算出U˜u和U˜l的离散序列在x轴和y轴的分量U˜uxi、U˜uyi、U˜lxi和U˜lyi(i=0,1,…,N-1),则对应的离散方程为
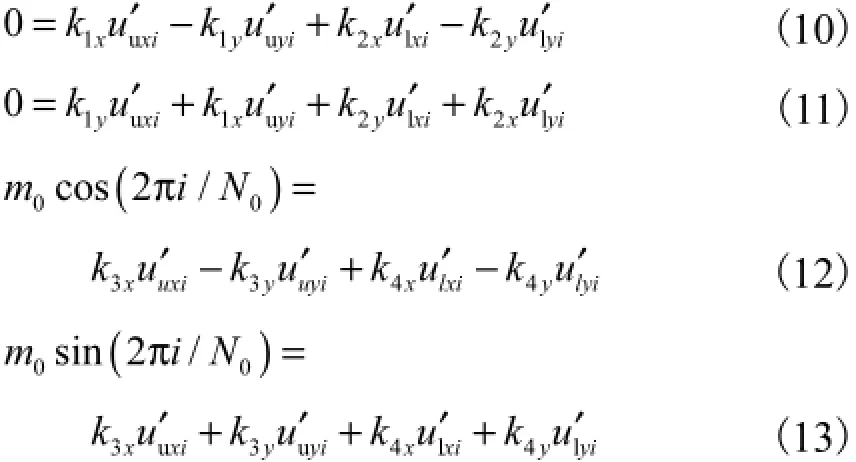
式中

3.2 基于最小二乘的影响系数求解算法
考虑形如y=ax1+bx2+cx3+dx4的等式,设其中yi、x1i、x2i、x3i、x4i为测量值,i=1,2,3,…,m,m为测试数据的点数.该式的方差为
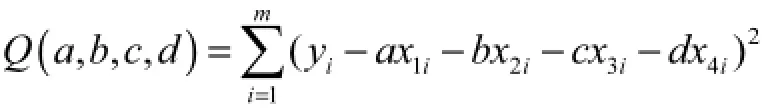
当Q(a,b,c,d)满足以下条件时方差最小,即

同理,考虑式(4)的方差计算,分别对系数k1x、k2x、k1y、k2y求导可得
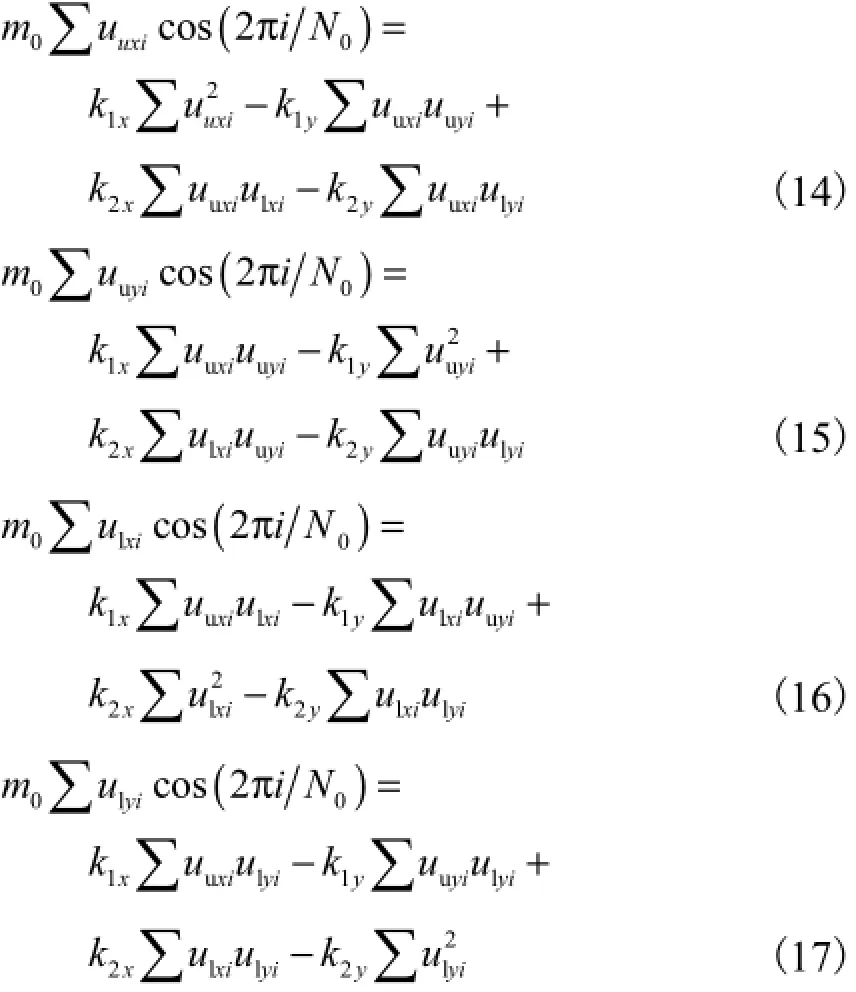
考虑式(10)的方差计算,分别对系数k1x、k2x、k1y、k2y求导可得
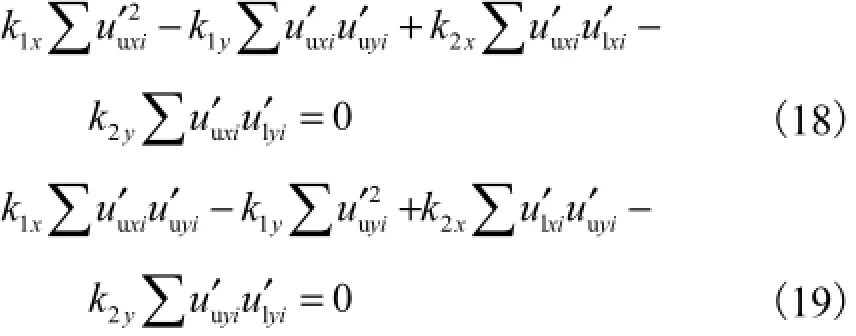

由式(18)+式(14)得到

由式(19)+式(15)得到

由式(20)+式(16)得到

由式(21)+式(17)得到

令yi(i=1,2,3,4)替代式(22)~式(25)中等号左边的部分,x1i、x2i、x3i、x4i(i=1,2,3,4)分别代替等号右边与系数k1x、k1y、k2x、k2y相乘的部分,从而将式(22)~式(25)改写为由此可计算得到影响系数k1x、k2x、k1y、k2y的值,用同样方法可计算出k3x、k4x、k3y、k4y的值.

3.3 实验验证及结果分析
实验过程中,分别在载重轮胎动平衡机的上轮辋0°和下轮辋180°位置安装100,g砝码,并将本算法的计算结果与直接求解复影响系数方程的结果进行比较.实验数据如表1和表2所示.
造成测量误差的原因主要有:动平衡机的制造与装配误差、轮胎与轮辋的配合误差、传感器与电荷放大器误差、以及各种现场设备对测试系统的干扰等.直接求解影响系数方程在很大程度上受到这些因素的影响,使计算出的影响系数偏离真值,不平衡量的计算误差随之增大.基于最小二乘的算法能够有效消除上述因素所引起的系统误差,因此计算精度优于直接求解法的结果.

表1 上轮辋安装砝码的测试结果Tab.1 Test results with weight on the upper rim

表2 下轮辋安装砝码的测试结果Tab.2 Test results with weight on the lower rim
依据不同的型号与质量等级,载重轮胎的不平衡量通常在50~300,g.实验结果表明,本文中所提出的标定算法具有很高的精度,砝码质量的测量误差在±1%范围内.本算法成功应用于具有自主知识产权的载重轮胎检测设备,该设备在轮胎生产线上经过长期工程实践验证,检测精度完全符合轮胎制造商的要求.
4 结 语
研究了载重轮胎动平衡机的参数标定算法.通过基于复影响系数的动力学方程来表征轮胎不平衡质量与主轴支承振动信号之间的对应关系,并提出了一种基于最小二乘的算法来计算影响系数.实验结果表明,提出的标定算法克服了影响系数方程直接求解法的不足之处,能够有效消除各种系统误差的影响,可实现很高的不平衡量测量精度,并成功应用于具有自主知识产权的载重轮胎检测设备中.
[1] 彭熙伟,李占宏,王 洪,等. 车轮动平衡的数字检测方法及其比较[J]. 汽车工程,2003,25(4):418,F003,329.
Peng Xiwei,Li Zhanhong,Wang Hong,et al. Digital detection methods for wheel dynamic balancing and their comparison[J]. Automotive Engineering,2003,25(4):3418,F003,329(in Chinese).
[2] 刘迎澍.基于数据变化率的胎面轮廓曲线还原算法[J].天津大学学报,2009,42(11):975-979.
Liu Yingshu. Changing rate based tire tread profile restoring algorithm[J].Journal of Tianjin University,2009,42(11):975-979(in Chinese).
[3] 巫上清. 动平衡机测量及远程监控系统研究[D]. 天津:天津大学电气与自动化工程学院,2009.
Wu Shangqing.Research on Measurement and Remote Monitoring System of Dynamic Balancing Machine[D]. Tianjin:School of Electrical Engineering and Automation,Tianjin University,2009(in Chinese).
[4] 陈振东. 载重轮胎动平衡机若干关键技术的研究[D].天津:天津大学电气与自动化工程学院,2007.
Chen Zhendong.Key Techniques Research for Loaded Tire Dynamic Balancing Machine [D]. Tianjin:School of Electrical Engineering and Automation,Tianjin University,2007(in Chinese).
[5] 张宏辉,张万利.基于影响系数法的车轮平衡机检测系统[J]. 机械设计与制造,2007(7):167-168.
Zhang Honghui,Zhang Wanli. A detecting system for wheel balancer based on the effect coefficient method [J].Machinery Design and Manufacture,2007(7):167-168(in Chinese).
[6] 都 强,杭柏林.最小二乘法在多传感器测量标定中的应用[J].传感技术学报,2005,18(2):244-246.Du Qiang,Hang Bailin. Application of least squares in multisensor measure specifying[J]. Chinese Journal of Sensors and Actuators,2005,18(2):244-246(in Chinese).
[7] Hang B L,Sun L M. Instrumentation model and data processing of tire dynamic balance using multi-sensors [C]//Proceedings of the 3rd International Conference on Innovative Computing Information and Control.Dalian,China,2008:531.
[8] Moon J D,Kim B S,Lee S H. Development of the active balancing device for high-speed spindle system using influence coefficient [J]. International Journal of Machine Tools and Manufacture,2006,46(9):978-987.
[9] 刘 健,潘双夏,杨克己,等.动平衡机系统误差分析及标定方法研究[J]. 组合机床与自动化加工技术,2002(4):1-4.
Liu Jian,Pan Shuangxia,Yang Keji,et al. Study on calibration method and system error compensation of balancing machines[J]. Modular Machine Tool and Automatic Manufacturing Technique,2002(4):1-4(in Chinese).
[10] 刘 健,潘双夏,杨克己,等. 全自动动平衡机关键技术研究[J]. 浙江大学学报:工学版,2006,40(5):777-782.
Liu Jian,Pan Shuangxia,Yang Keji,et la.Research on key technologies of automated balancing machines[J]. Journal of Zhejiang University:Engineering Science,2006,40(5):777-782(in Chinese).
[11] 伍良生,李 俊,肖毅川,等. 基于盘状加工件在线动平衡技术的研究[J]. 北京工业大学学报,2011,37(6):811-815.
Wu Liangsheng,Li Jun,Xiao Yichuan,et al. Online dynamic balancing technique basing on discal work [J]. Journal of Beijing Polytechnic University,2011,37(6):811-815(in Chinese).
[12] Zhou S,Dyer S,Shin K,et al. Extended influence coefficient method for rotor active balancing during acceleration[J]. Journal of Dynamic Systems,Measurement and Control,Transactions of the ASME,2004,29(1):219-223.
[13] Untaroiu C D,Allaire P E,Foiles W C. Balancing of flexible rotors using convex optimization tech-niques:Optimum min-max LMI influence coefficient balancing [J]. Journal of Vibration and Acoustics,2008,130(2):1-5.
[14] Tseng C H Y,Shih T W,Lin J T. Dynamic balancing scheme for motor armatures [J]. Journal of Sound and Vibration,2007,304(7):110-123.
[15] Zhang Jian,Wu Jianwei,Ma Zhiyong. Hierarchical bayesian calibration and online updating method for influence coefficient of automatic dynamic balancing machine[J]. Chinese Journal of Mechanical Engineering,2009,22(6):876-882.
Complex Influence Coefficients Based Calibration Algorithm of Tire Dynamic Balance Testing Machine
Liu Yingshu1,Yin Jianhua1,Wu Shangqing2
(1. School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China;2. Research Institute of Microelectronics,ZTE Corporation,Shenzhen 518052,China)
Dynamic balance performance is a standard specification to determine whether a tire “qualifies”. The system parameter calibration algorithm, a key technology of tire dynamic balance testing machine, is investigated elaborately. The tire-rim-spindle dynamics is demonstrated by the complex influence coefficient plant model, and a least square based calibration algorithm is developed to calculate influence coefficients. Additional weight is added to the rim to verify the accuracy of parameter calibration. Experimental results show that the mass calculation error of unbalanced weight is within the range of ±1%, which demonstrates that the presented algorithm is more effective in correcting instrumental systematic errors than traditional methods. As a result, the derived influence coefficient plant model is more accurate in demonstrating the relationship between tire unbalanced mass and spindle bearing vibration signals.
dynamic balance testing machine;parameter calibration;complex influence coefficient
TQ330.4
A
0493-2137(2013)06-0565-06
DOI 10.11784/tdxb20130616
2011-11-29;
2012-05-03.
天津市20项自主创新产业化重大基金资助项目.作者简介:刘迎澍(1971— ),男,博士,副教授.
刘迎澍,liu_ysh@tju.edu.cn.
