移圈针扩圈片安装过程的应力场模拟

程 静，丁 浩，朱世根

（东华大学 机械工程学院，上海 201620）

移圈针扩圈片安装过程的应力场模拟

程 静，丁 浩，朱世根

（东华大学 机械工程学院，上海 201620）

为了解决移圈针上扩圈片安装过程中出现的冲头崩裂和安装不牢固问题，采用有限元软件ABAQUS对不同倒角半径的冲头在扩圈片安装过程中的应力应变场，及扩圈片和其安装槽之间接触力的影响规律进行模拟和分析.结果表明，随着倒角半径的增大，冲头上所受的应力呈现整体下降的趋势，扩圈片与其安装槽的接触应力也在减小.经比较分析得知，最佳的倒角半径为0.11 mm，此时，既能保证冲头拥有较长的使用寿命，又能保证扩圈片的安装牢固度.将模拟结果应用于移圈针的实际生产，单枚冲头的使用寿命与之前相比提高了5倍，且扩圈片的安装牢固率达到了100%.

移圈针；冲头；ABAQUS；应力场；接触应力

随着机械技术和电子技术的不断发展，电脑横机逐渐取代了手动横机成为羊毛衫生产行业的主要机种［1］，这对作为电脑横机上标准件之一的移圈针提出了越来越高的质量要求.

目前电脑横机上的装机移圈针大多进口于德国、韩国等生产技术较为成熟的国家，国内移圈针的制造虽已初具规模，但移圈针的生产稳定性差，成品率较低.

移圈针工作时需要完成成圈和移圈，因此，扩圈片是不可缺少的关键零件.因针杆和扩圈片性能参数的差异，需要在各自完成热处理后进行组装.由于两者材料的特殊性以及相关位置精确要求，使得焊接方式无法完成组装，因此，采用类似于铆接的机械装配方式将两者安装为一体.在扩圈片的安装过程中常出现扩圈片安装不牢固、针杆和扩圈片产生不同程度的变形以及冲头出现裂纹或破碎导致使用寿命较低等现象.

为解决上述问题，有必要对扩圈片安装过程中冲头、针杆和扩圈片上的应力应变场的规律性进行研究.本文采用有限元软件ABAQUS对不同倒角半径的安装冲头进行安装模拟，通过分析安装过程中安装冲头上应力场分布及扩圈片和针杆的接触力，得出不同的倒角半径对冲头的使用寿命和扩圈片安装牢度的影响，选择最佳的冲头倒角半径，为实际的安装过程提供了技术依据.

1 物理模型及边界条件的确定

1.1 物理模型

扩圈片的安装是扩圈片、针杆、安装冲头和下模具4体间相互作用的过程，如图1所示.首先将扩圈片放在针杆上的安装槽内，通过扩圈片上的定位孔和槽内定位销的配合来保证二者之间的相互位置.将两者放入下模具内，依靠安装冲头提供的大于针杆金属屈服强度的安装力，使针杆金属在塑性条件下进行体积转移［2］，形成如图2所示的压痕，利用近似于铆接的形式将扩圈片固定在针槽中.

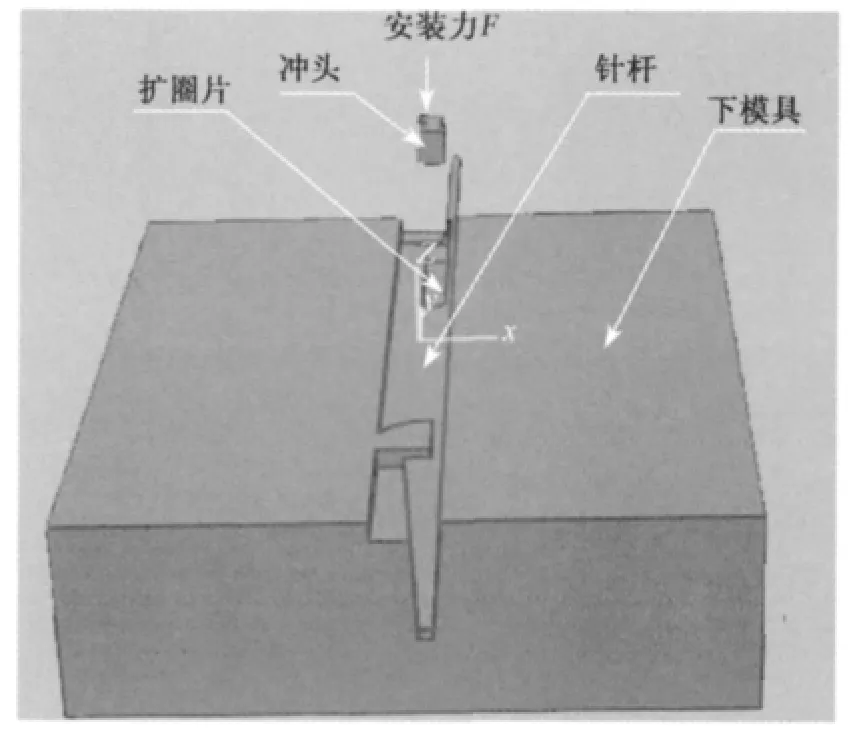
图1 扩圈片安装示意图Fig.1 The spring's installation

在扩圈片的安装过程中，针杆和扩圈片可能产生塑性变形.因此，在不考虑温度对材料变形影响的前提下，针杆和扩圈片均采用弹塑性材料模型.钢的普朗特-劳依斯本构关系［3］如式（1）所示.

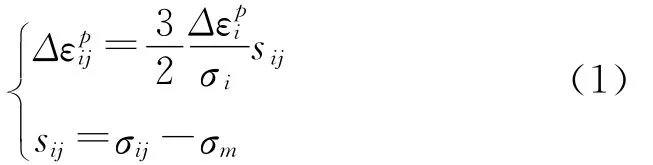
图2 针杆上的压痕示意图Fig.2 Indentation in needle

其中：σi为应力为i和j方向上的塑性应变增量为i方向上的塑性应变增量；σij为参考应力；σm为平均正应力，sij为参考应力与平均应力的差值，i和j取值为1和2.

在安装时针杆和扩圈片均已进行热处理，因此，冲头需要采用硬度更高且在安装过程中不会屈服的材料.本文采用了 WC-Co类硬质合金割制冲头，在数值模拟时采用弹性材料模型近似替代冲头的物理模型.另外，下模具采用了与冲头近似的材料模型，即弹性材料模型.弹性材料的物理本构方程关系［4］如式（2）所示.

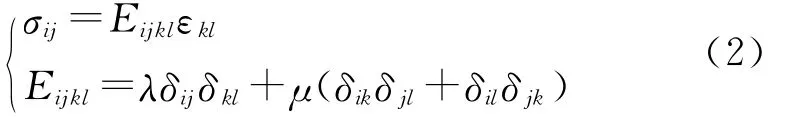
其中：i，j，k，l取值范围为1，2，3，4；σij为应力；εkl为相应的应变量；λ和μ为Lame系数.

1.2 边界条件

边界条件的确定是实现数值模拟计算的关键.扩圈片的安装是下模具、针杆、扩圈片和冲头4体间相互作用的过程，因此，本文中边界条件的确定如下所述.

下模具装在冲压机工作台上，用定位销和螺栓进行定位和锁紧，在机架这一固定坐标系中，y和z方向可以按照第二类边界条件处理，即位移为0.而在x方向上下模具只与针杆接触，符合作用力与反作用力的关系，属于第一类边界条件，此时Fx＝F1，其中F1为针杆与下模具的作用力.

移圈针的针杆装在下模具沟槽内，针杆底面与沟槽底面接触，针杆的侧面与下模具沟槽两侧之间初始有间隙存在.在冲压过程中，局部可能产生接触，针杆的侧面和下模具沟槽侧面在x方向始终是作用力等于反作用力的关系，即边界条件为Fx＝F1＋F2，其中F2是扩圈片侧面与针杆上安装槽侧面的接触力.针杆在z方向受到冲头的安装力F的作用.

扩圈片被安装在针杆上的安装槽内，最后被由冲头在针杆的扩圈片槽侧面压出的凸点夹紧，扩圈片的底面与槽底面一直接触，而上表面可能被凸点局部覆盖，存在接触关系.

冲头为工字型，整体安装在夹持系统中，受到夹持系统给予的位移边界条件，冲头的底面与针杆上的扩圈片槽侧面接触，受到针杆对其的反作用力，其大小为F，方向向上；中间部分与扩圈片的上表面接触，而接触关系随着冲压过程的进行而产生或消失.

2 数值模拟的关键技术

2.1 有限元算法的选用

有限元数值分析中，常用的算法有Lagrangian算 法、Euler 算 法、Arbitrary Lagrangian-Euler（ALE）算法以及Smooth Partcle Hydrodynamic（SPH）算法等，每一种算法各有优劣，所应用的范围也有所不同.如Lagrangian算法能够非常精确地描述结构边界的运动，常用于处理小变形问题，而对于大变形问题，由于自身特点的限制，将会出现严重的网格畸变现象，不利于计算的进行.Euler算法是处理大变形问题的一种非常有效的手段，但在数值模拟过程中，各个迭代过程中计算数值的精度较低.

在扩圈片安装过程中，压痕处金属发生弹塑性变形，属于局部大变形问题.在数值模拟过程中，此处的六面体网格会发生严重的畸变，使计算由于收敛问题而中断，同时由于需要较高的模拟精度，单纯选用Lagrangian算法或Euler算法无法解决网格畸变和高精度问题.对于大变形且需要精确模拟的问题，ALE算法是最有效的算法.这种算法兼具Lagrangian方法和Euler方法的特长，即在模拟过程中网格可以根据定义的参数在求解过程中适当调整位置，使得网格不会出现严重的畸变，同时又能保证足够的模拟精度，使得计算更高效、更稳定［5］.

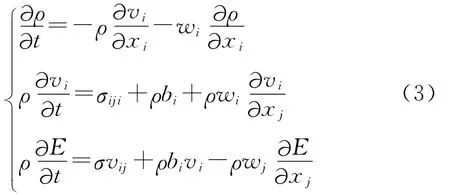
针对ALE方法的控制方程［6］（质量、动量和能量守恒方程）如式（3）所示：其中：ρ为密度；v为物质速度；w为对流速度；b为单位体积物体上所受到的力；σ为柯西应力张量；E为能量；t为时间；i和j取值范围为1和2.

在数值模拟过程中，只有当冲头接触到针杆表面并形成压痕的过程中，金属才产生严重的变形，其余过程如冲头从原始位置到开始接触针杆表面以及冲头返回原始位置的过程中，网格均只产生极小的变形.由于ALE算法的计算成本较高，因此只在冲头接触到针杆表面形成压痕的过程中采用了ALE算法，其余过程均采用Lagrangian算法.

2.2 Partition Cell分割技术

实体模型的离散化是进行数值模拟的重要步骤，本文采用C3D8R单元类型进行网格划分.对于安装冲头而言，由于存在大量的倒角使其形状非常不规则，因此在使用智能网格划分功能之前，需采用Partition Cell功能对冲头进行分割，将每一个圆角都当作一个完整的个体分割出来，保证每个个体均是规则的形状.分割后的冲头如图3（a）所示，然后采用C3D8R单元类型进行网格的划分.针杆上虽无圆角，但其形状不规范，在划分网格之前，同样需要对模型进行分割，分割后的针杆如图3（b）所示.

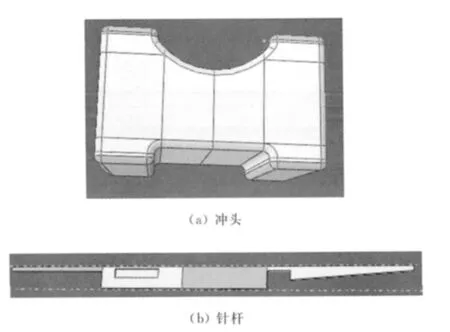
图3 冲头和针杆分割后的模型图Fig.3 Punch and needle bar for partition

对于分割后的零部件，不仅可以选用精度较高的六面体网格，而且可以在不同的区域布置不同的网格密度.同时，Partition Cell功能为无法采用智能网格划分的复杂模型的网格划分提供了一个有效的解决方法.

3 数值模拟结果及分析

3.1 安装冲头应力场的模拟

在安装冲头宽度为2.4 mm和倒角半径为0.11 mm的条件下，用ABAQUS软件对扩圈片的安装过程进行模拟.在本次模拟中扩圈片的安装主要是依靠冲头的运动来实现，将冲头一个周期内的运动过程分解为3个step，以便载荷的施加.step 1指冲头从原始位置运动到针杆表面；step 2指冲头从针杆表面继续向下运动至一定深度，以便形成压痕；step 3指冲头从step 2的结束返回至原始位置，结束一个周期的运动.

图4为安装冲头所有节点在step 2中某一位置下数值模拟得到的应力分布情况.由图4可知，安装冲头的主要受力区域为压痕所对应的4个局部区域，这与试验过程中冲头的失效部位是一致的，图5为破碎的冲头图片.在扩圈片安装过程中，在正常情况下工字形安装冲头的中间部位并未与针杆或扩圈片接触，属于不受力区域，而冲头上部靠近侧面0～0.2 mm宽度范围内的区域，则是直接与针杆上的金属相接触并迫使金属流动形成压痕，因此是冲头上的主要受力区域.在冲头运动过程的3个step中，step 2是安装冲头承受应力的主要时间段，所受应力值主要集中在1 081～1 709 MPa.

3.2 不同倒角半径时冲头应力场的模拟

为了研究不同倒角半径对安装冲头应力场的影响，在保证冲头宽度、网格等级等参数不变的前提下，当倒角半径分别为0，0.02，0.04，0.05，0.07，0.09，0.10，0.11，0.12，0.13，0.14 mm时，模拟安装冲头上应力场的分布情况.

图6为不同倒角半径的冲头在step 2中同一时间增量步时的应力场分布趋势图.由图6可知，冲头边角从无倒角到有半径为0.02 mm的倒角时，主要应力值从1 608 MPa剧增到5 208 MPa.究其原因，主要是理论上冲头的边角处是两个侧面的交线，则曲率半径应为0 mm，但实际上冲头的边角处是一个圆弧［7］，如图7所示.理论上的冲头边角处为一条边，因此形成同样的压痕，作用在冲头上的反作用力较小，所以当倒角半径为0 mm时，冲头上的应力值较小.在实际制造过程中，硬质合金材料的零件一般在边角处存在0.02～0.03 mm 的半径［8］，所以当冲头边角处的倒角半径为0.02 mm时，由于应力集中现象较严重使得应力值非常大，此时的应力值相当于无倒角冲头的应力值.当倒角半径在0.02～0.11 mm范围内逐渐增大时，冲头上主要受力区域的应力值逐渐降低；倒角半径为0.12～0.14 mm时，随着半径的增大，安装冲头主要受力区域的应力值呈现平稳上升的趋势.倒角的存在使得冲头边角处应力集中的现象得以缓解，应力值减小.但当倒角半径增大到一定值时，安装冲头上实际参与压制压痕的面积减小了，使得在同样的安装力作用下应力值有所增大.

图6 不同倒角半径的冲头在step 2中时间增量步为0.5 s时的应力场分布Fig.6 The stress distribution in different chamfer radius’punch at incrementation step being 0.5 s of step 2

图7 安装冲头边角图Fig.7 The corner edge in punch

在扩圈片的安装过程中，冲头的主要失效形式是出现裂纹或破碎，因此，应将冲头上所受的应力值作为其使用寿命长短的主要评价标准.由模拟结果可知，当倒角半径为0.11 mm或0.12 mm时，冲头上的应力值主要集中在1 091～1 727 MPa.由文献［9］可知，经放电等离子技术烧结出的 WC-Co类普通硬质合金的抗拉强度可达到1 860 MPa，当倒角半径为0.11 mm或0.12 mm时，冲头上的应力值在WC-Co类硬质合金钢所能承受的范围内，此时安装冲头是有较高的使用寿命.

3.3 倒角半径对扩圈片安装牢度的影响

倒角半径的选择不仅应使安装冲头具有较长的使用寿命，还应保证扩圈片的安装牢度，因此，扩圈片的安装牢度是选择冲头倒角半径的另一主要参考标准.将安装过程结束后扩圈片与针槽的接触力作为扩圈片能否被装牢的衡量标准，由文献［10］可知，接触力应大于85 N.

扩圈片与针槽的接触力随冲头倒角半径变化的数值模拟结果如图8所示.由图8可知，随着倒角半径的增大，扩圈片与针槽的接触力逐渐降低，但接触力的大小均集中在130～200 N，此值均可保证扩圈片被安装牢固.由于扩圈片工作时需要反复地张开-闭合，这种特殊的工作状态使得扩圈片的脱落成为移圈针非正常失效的主要原因之一，因此，要求移圈针上的扩圈片必须具备绝对的安装牢度，即在一定范围内扩圈片和针槽的接触力越大越好.当倒角半径为0.11和0.12 mm时，二者的接触力差值为16 N，所以倒角半径为0.11 mm时更合适.

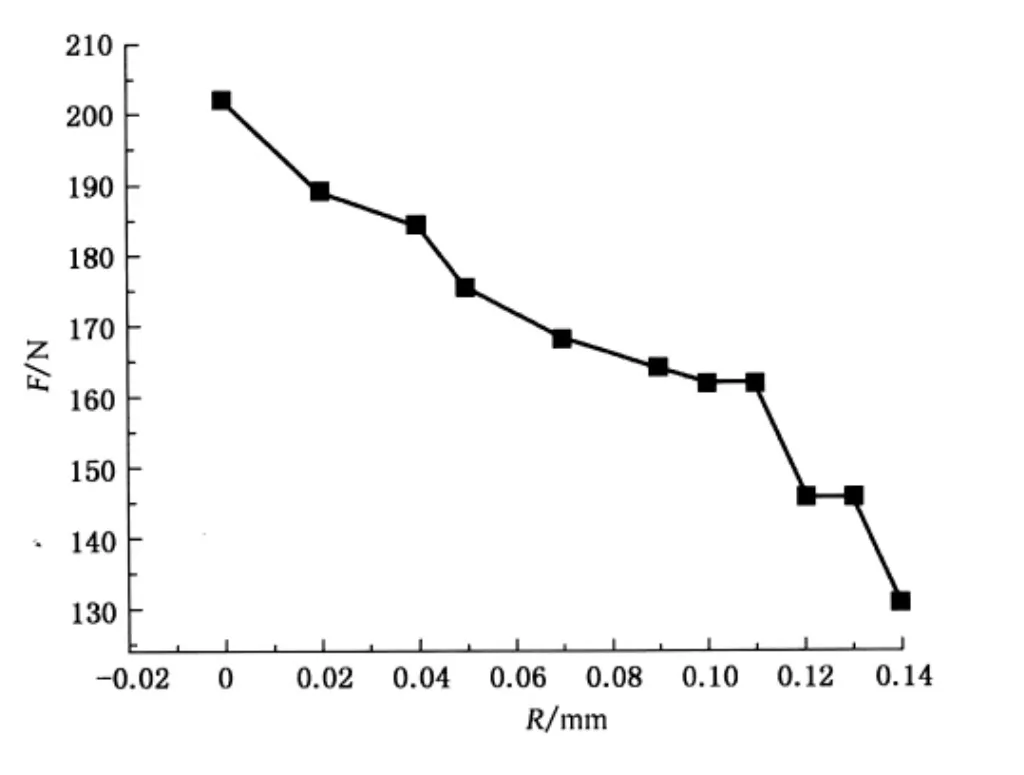
图8 不同倒角半径时的接触力Fig.8 The contact force in difference chamfer radius

综合倒角半径对安装冲头应力场分布和扩圈片与针槽接触力的影响，最适宜的倒角半径为0.11 mm，此时既能保证安装冲头的使用寿命，又能使得扩圈片被牢固安装在针槽中.

将以上的研究结果应用于实际生产中，对冲头进行边角控制，有效地解决了冲头的崩裂和扩圈片安装不牢固问题.实际应用表明，在针杆和扩圈片尺寸符合技术要求的前提下，单枚冲头的使用寿命与之前相比提高了近5倍，且扩圈片的安装牢固率达到100%.即通过选用合适倒角半径能很好地保证冲头的使用寿命和扩圈片安装牢度.

4 结 语

（1）随着冲头倒角半径的增加，扩圈片安装时冲头所受应力整体呈大幅下降趋势，而倒角半径为0.12～0.14 mm时，其缓慢上升，即随着倒角半径的增大，冲头的使用寿命可得到提高.

（2）扩圈片与针槽的接触力随着倒角半径的增大呈整体下降趋势，即随着倒角半径的增大，扩圈片的牢固度降低.

（3）综合考虑倒角半径对冲头使用寿命和扩圈片安装牢度的影响，得知冲头边角处的倒角半径最佳值为0.11 mm.

（4）将模拟结果应用于实际生产中，冲头的使用寿命与之前相比提高了近5倍，且扩圈片的安装牢固率达到100%.

［1］刘国华.针织大圆机和横机的销售量［J］.国际纺织导报，2002（4）：46-47.

［2］缪宏，左敦稳，张敏，等.飞机起落架高强度钢内螺纹冷挤压成形金属流动规律研究［J］.中国机械工程，2010，21（14）：1714-1715.

［3］SHEN L J.Studies on constitutive relations of isotropic and kinematic hardening materials at finite elastic-plastic deformation［J］.宁波大学学报：理工版，2001，14（4）：7-19.［4］程尧舜.弹性力学基础［M］.上海：同济大学出版社，2009：54-63.

［5］USAMA U，XIE L J，WANG X B.Finte element analysis for chip formation in high speed turning operations by arbitrary Lagrangian Eulerian method［J］.Chinese Journal of Mechanical Engingeering，2006，19（4）：480-482.

［6］LIU W K，CHEN J S，BELYTSCHKO T，et al.Adaptive ALE finite elements with particular reference to external work rate on frictional interface ［J］.Comput Meths Appl Mech Engrg，1991，93（2）：189-216.

［7］原一高，朱世根.纤维切割过程中切断刀锋利性能分析［J］.纺织学报，2004，25（6）：34-35.

［8］XIE Y F，WANG X Q，CHEN L D，et al.Preparation of superfine-cemented carbide by spark plasma sintering［J］.Journal of Wuhan University of Technology：Material Science Edition，2006，21（1）：42-45.

［9］赵世贤，宋晓艳，王名胜，等.预处理工艺对放电等离子烧结超细晶WC-Co硬质合金组织和性能的影响［J］.稀有金属材料与工程，2010，39（5）：896-901.

［10］FZ／T 97005.3—1991针织用舌针横机针［S］.

Stress Field Simulation on the Spring Installation Process of Transfer-Needle

CHENGJing，DINGHao，ZHUShi-gen

（College of Mechanical Engineering，Donghua University，Shanghai 201620，China）

To solve the cracking of the punch and the shedding of the spring in the process of spring installation，influence law of the punch's chamfering radius on the stress value and contact force between spring and groove was simulated and analyzed with the finite analysis software of ABAQUS.The results showed that with the increase of the chamfering radius，the stress values in punch followed a whole descending trend and the contact force gradually decreased.The longest service life for punch and the optimum installing effect for spring were obtained in the punch with a chamfering radius of 0.11 mm.The results were applied and examined in the actual production of transfer-needle，a punch's service life increased 5 times longer than before，and the spring's installation rate reached 100%.

transfer-needle；punch；ABAQUS；stress field；contact stress

TH 164

A

2012-04-09

“十一五”国家科技支撑计划“电脑横机移圈针高性能化关键技术研究”资助项目（2007BAF24B04 4）

程 静（1986—），女，河南周口人，硕士研究生，研究方向为机械制造及其自动化.E-mail：chengjing04241＠126.com

丁 浩（联系人），男，副教授，E-mail：dinghao＠dhu.edu.cn

1671-0444（2013）02-0214-05