动不平衡激励下光滑非线性车辆摆振系统建模分析

胡 辰，卢剑伟，许 生

(合肥工业大学 机械与汽车工程学院，合肥 230009)

汽车前轮摆振可分为强迫振动和自激振动，前者由周期性干扰力引起，摆振频率与作用在车轮上的干扰力频率一致;后者不需要周期性干扰力，偶遇冲击(如路面凸凹不平)发生偏转之后，车轮的振动并没有衰减，而是变成稳定持续的振动。

前轮摆振对汽车动力性、燃油经济性、操纵稳定性、行驶平顺性及行车安全都有极大的负面影响，国内外学者对摆振机理及控制进行了大量研究，取得了很多有价值的成果。Stépán 等［1］基于作用在轮胎上的外力矩所产生的机械功考察了自激摆振的条件;Demic［2］考虑转向系与悬架耦合分析了转向系参数对自己摆振的影响;Kimura［3］通过试验和仿真分析了某轻卡自激摆振问题;Takács等［4］分析了轮胎迟滞效应对摆振的影响。宋健等［5］讨论了前轮定位参数与轮胎特性对摆振的影响;林逸等［6］以常微分方程稳定性理论为基础，阐明了自激型摆振是一种Holf分岔后出现的稳定极限环运动。

本文在前期自激振动研究的基础上对车轮动不平衡激励下的三自由度光滑非线性摆振系统动力学响应进行分析，并通过和前期自激振动研究的结果进行对比以明确动不平衡激励对摆振系统动力学行为的影响，为转向轮摆振控制提供支持。

1 考虑动不平衡的摆振动力学模型

设汽车在平坦路面上以速度v直线行驶，oxyz为模型坐标系，其中x轴指向汽车前进方向，z轴垂直向上，y轴指向汽车左侧，前桥质心为坐标原点。

为简化分析过程，仅考虑右前轮有偏心，并假定偏心力作用于车轮中性面上。忽略车轮弹性变形及其它参数的影响。对于前轮定位参数，只考虑对摆振影响较大的主销后倾角，则该系统有3个自由度:右前轮转角θ1、左前轮转角θ2及前桥侧摆角φ，模型示意图见图1。

图1 三自由度摆振模型示意图Fig.1 Schematic diagram of3 DOF model of shimmy

基于以下假设建立系统动力学模型:

(1)不考虑运动副间隙、干摩擦等因素，只考虑轮胎侧偏特性这一光滑非线性因素。

(2)忽略风阻、纵拉杆及转向器质量对系统的影响，转向纵拉杆到方向盘简化为一弹簧阻尼器。

(3)不考虑轮胎滑移，前后轮侧向力相等。

(4)汽车行驶方向及车速不变。

图2 车轮动不平衡力示意图Fig.2 Schematic diagram of dynamic unbalance on the wheel

由于滚动阻力力矩和翻转力矩至多在转向轴上产生正弦分量，是二阶次要影响，在转向系力矩分析中可以忽略，因此动不平衡对摆振的影响主要体现在回正力矩上［7］。主销后倾角是形成转向轮回正力矩的重要因素，如图2所示，当存在偏心的车轮转动时，将产生随旋转方向不断改变的周期性的离心力，其大小为:

式中:m0为偏心质量;e为偏心距;ω为车轮转动圆频率。当旋转的离心力和主销不平行时，车轮上便产生了周期性的回正力矩Td:

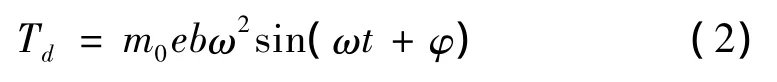
式中:b为主销到车轮中心面的距离;φ为偏心力的初始相位角;

结合上述分析，可得到右轮动不平衡激励下摆振系统的运动微分方程为:

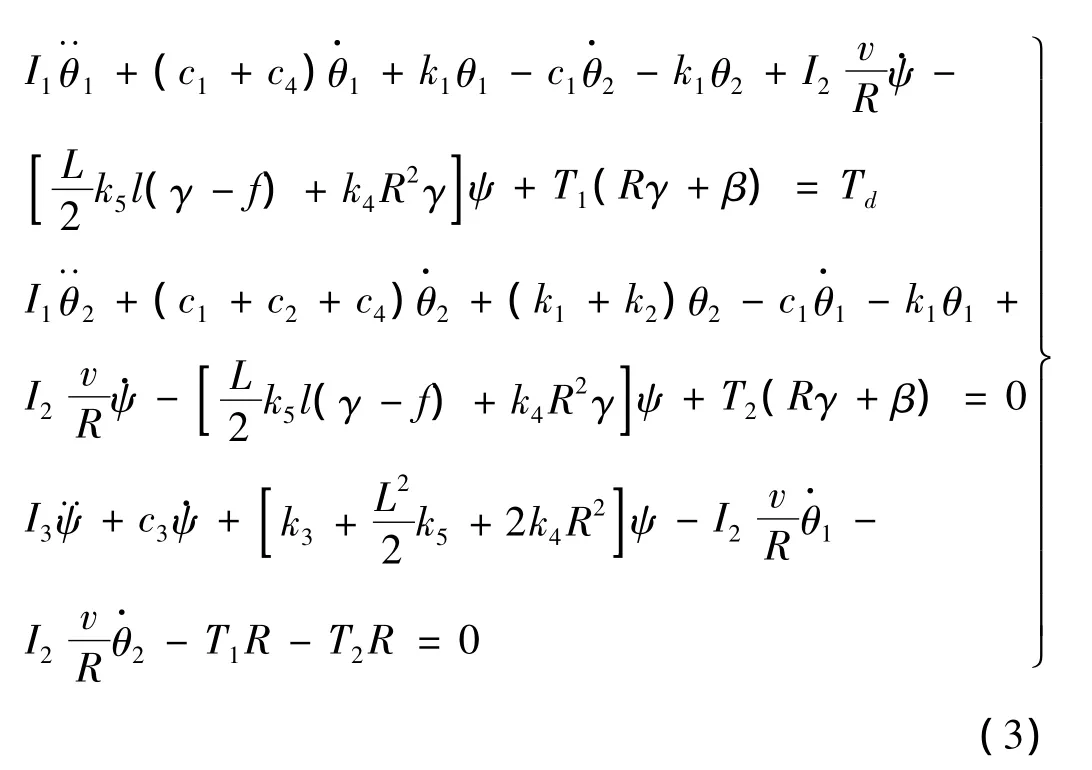
式中:参数含义及取值见表1，前轮侧向力T1、T2由魔术公式给出:

式中:α2，α1为左、右车轮的侧偏角，Sx，Sy，C，D，E 为常数。据文献［6］，取 Sx=0，Sy=0，B=9.302 rad－1，C=1.29，D= －5.25 kN，E= －0.801，轮胎侧偏角与车轮摆角之间约束为:

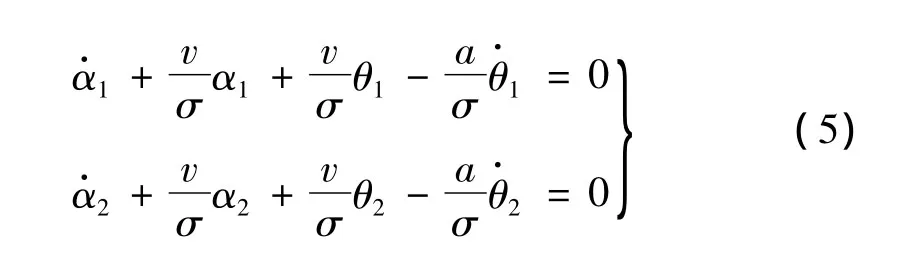
2 仿真分析及结果

假定动不平衡由车轮重心偏移引起，偏心质量m0即为车轮质量30kg，并设右轮上动不平衡力的初始相位角φ=0。应用四阶龙格－库塔法进行数值求解，考察右轮上不同偏心距的动不平衡激励对摆振系统响应的影响。

图3 右轮摆角随车速的分岔特性Fig.3 Bifurcation characteristics of swing angle on right wheel

图3(a)～3(c)分别为偏心距 e=0.4，4，40 mm 时右轮随车速变化的分岔图;图3(d)为无动不平衡激励，但右轮存在初始扰动摆角为0.01 rad时，右轮摆角随车速的分岔图。从图中摆振车速区间(47－70 km/h)内的分岔特性可以看出，当偏心距为0.4 mm时，由于激励强度较小，车轮摆角的分岔特性和无外激励时的自激振动相似，但运动形态要复杂些;当偏心距为4 mm时，摆振形态更加复杂，但在车速约为52 km/h处出现了一个跃变的窗口，该窗口内的摆振形态比较简单，而摆振幅值大幅高于其他车速下的幅值;偏心距达到40 mm时，摆振幅度虽大幅增加，但摆振形态反而变得简单了。在此需要说明的是，虽然车轮实际偏心距通常不会达到40 mm，但是该分析结果无疑能够说明对于给定车型参数，存在一个临界偏心距，并伴随着摆振车速内进入单周期运动且摆振幅度大幅增加，如果车型参数发生变化，这个临界偏心距也数值会变化。

表1 某非独立悬架汽车摆振模型参数Tab.1 Parameters of a dependent suspension vehicle

此外，偏心距为4 mm时，在原来并不摆振的高车速区间(70～110 km/h)也开始有了微小的摆振，对比低车速区间(10～47 km/h)的运动形态可以发现，高速时摆振现象要比低速时明显;偏心距为40 mm时，车轮在整个车速区间内均发生不同程度的摆振，但高速区间摆振幅值比低速区间的大。

为进一步考察车轮摆角的运动特性，结合时间历程、功率谱、相图和庞加莱截面对车速为55 km/h时的右轮摆角进行分析。图4～图6分别为偏心距e=0.4，4，40 mm时右轮摆振运动特性;图7为无动不平衡激励，但右轮存在初始扰动摆角0.01 rad时右轮摆角。

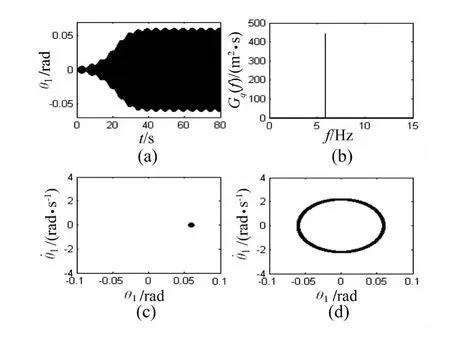
图4 右轮摆角响应(e=0.4 mm)Fig.4 Dynamic response of right front wheel(e=0.4 mm)

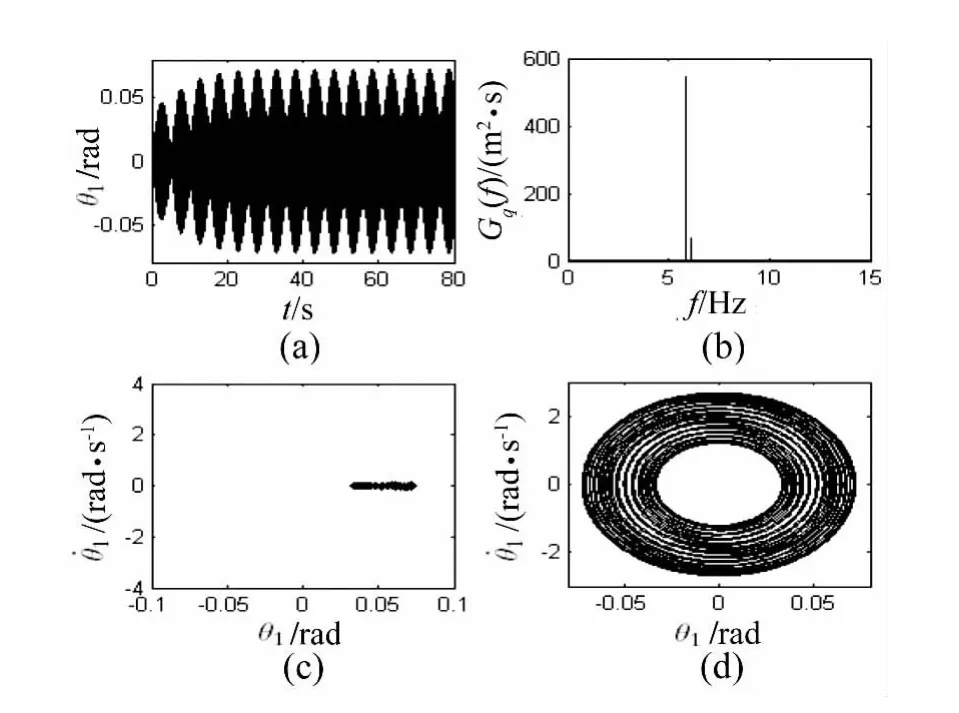
图5 右轮摆角响应(e=4 mm)Fig.5 Dynamic response of right front wheel(e=4 mm)

从图4～图6可看出，由于轮胎的非线性特性，偏心距为0.4 mm和4 mm时，外激励作用下摆振均呈现拟一周期状态，比图7自激振动时的单周期运动要复杂，从时域图和频谱图看，由于运动中同时包含了自激频率成分和强迫振动频率成分，且两个频率相近，这两个状态下振幅随时间作周期性缓慢变化，即发生了拍振现象。但当偏心距再增加为40 mm时摆振运动反而回到了类似自激振动的简单的单周期运动。

图6 右轮摆角响应(e=40 mm)Fig.6 Dynamic response of right front wheel(e=40 mm)

图7 自激振动下的右轮运动特性Fig.7 Motion characteristics of right wheel under the self-excited vibration

强迫振动的摆振形态是由外激励和系统自身结构特性共同决定的，而系统自身结构特性体现在响应的自激振动频率成分中，摆振中是自激振动成分占主导，还是外激励引起的强迫振动成分占主导，对摆振的形态有重要意义。图8(a)～图8(c)分别为动不平衡偏心距e=0.4，4，40 mm，外激励频率、最大功率谱对应的频率和无外激励时的振动频率随车速变化对比图，通过对其频率成分的分析以期解释上面的摆振现象。

从图8a可以看出，偏心距为0.4mm时，在摆振区间之外，有外激励作用时的最大功率谱对应的频率和系统自激频率是一致的，这和自激振动下，摆振频率和车速几乎无关形成了对比。同时，摆振区间内的摆振最大功率谱对应的频率和自激振动状态时的摆振频率一致，这说明在偏心距较小时，此区间内系统自身结构产生的自激振动是振动的主导因素，这解释了为何图3a中的摆振区间内的摆振形态和自激振动时的分岔图3(d)的摆振形态极其相似;当车速约为52 km/h，强迫振动和自激振动频率相同，根据拍振理论此时振幅达到最大值，这和图3(a)中得到的结果一致。

从图8(b)可以看出偏心距增加为4 mm时，摆振区间内大部分车速下摆振的最大功率谱所对应的频率和自激频率保持一致，但随着外激励的强度的加大，出现了和外激励频率一致的区间窗口，这解释了为何分岔图3(b)中车速为52 km/h处出现跳跃的窗口，幅值突然增大，运动形态变为单周期运动。

从图8(c)可以看出偏心距再增加为40 mm时，整个车速区间内的最大功率谱所对应的频率都和激励频率一致，这解释了为何图3c中整个车速区间内都呈现单周期运动。从这三个不断加大偏心距的频率对比图可以看出摆振由系统自身结构起引起的自激振动成分占主导因素逐步到由外激励占主导因素的变化过程。

图8 不同偏心距下的频率对比Fig.8 Comparison of frequencies under different eccentricity

3 结论

(1)考虑动不平衡激励的车辆摆振系统，通常情况下其摆振响应中同时包含强迫摆振与自激摆振两种成分。

(2)动不平衡激励作用下的摆振系统响应分析结果显示，强迫摆振与自激摆振两种成分在摆振系统响应中所占比例主要取决于车速和动不平衡激励大小。

(3)和自激振动相似，强迫振动下系统也有一定的摆振车速区间，高车速区间内的摆振比低车速区间内的摆振明显，因此研究动不平衡对行驶车速较高的车辆有更重要的意义。

(4)当强迫振动的频率和自激振动频率相近时，会发生拍振现象，即车轮摆角的振幅会随时间作周期性缓慢变化。

［1］Stépán G，Goodwine B.Chaotic motion of wheels［J］.Vehicle System Dynamics，1991，20(6):341 －351.

［2］DemiéM.Analysis of influence of design parameters on steered wheels shimmy of heavy vehicle［J］.Vehicle System Dynamic，1996，26(5):343－362.

［3］Kimura T， Hanamura Y. Analysis of steering shimmy accompanied by sprung mass vibration on light duty truckfundamental mechanism［J］.JSAE Review，1996，17(3):301－306.

［4］Takács D，Orosz G，Stépán G.Delay effects in shimmy dynamics of wheels with stretched string － like tyres［J］.European Journal of Mechanics A/Solids，2009，28:516–525.

［5］宋 健，管迪华.前轮定位参数与轮胎特性对前轮摆振影响的研究［J］.汽车工程，1995，17(3):13－25.SONG Jian，GUAN Di-hua.The study of the influence of front wheel alignment patameters and tire characteristics on shimmy［J］.Automotive Engineering，1995，17(3):13 －25.

［6］林 逸，李 胜.非独立悬架汽车转向轮自激型摆振的分岔特性分析［J］.机械工程学报，2004，40(12)，187 －191.LIN Yi，LI Sheng.Bifurcation character analysis of self excited shimmy on steering wheel of independent suspension vehicle［J］.Chinese Journal of Mechanical Engineering，2004，40(12)，187 －191.

［7］Gillespie T D.Fundamentals of vehicle dynamics［M］.New York:Society of Automotive Engineers，2000.