Valid hydrodynamic interaction regions of multiple ships advancing in waves*

XU Yong (许勇), DONG Wen-cai (董文才)

Department of Naval Architecture, Naval University of Engineering, Wuhan 430033, China, E-mail: nancy23670@163.com

Valid hydrodynamic interaction regions of multiple ships advancing in waves*

XU Yong (许勇), DONG Wen-cai (董文才)

Department of Naval Architecture, Naval University of Engineering, Wuhan 430033, China, E-mail: nancy23670@163.com

(Received October 19, 2012, Revised January 16, 2013)

Based on the 3-D surface panel method combined with the translating-pulsating source Green function, an approximate approach is developed to solve the hydrodynamic interacting problem of multiple ships advancing parallel in waves. Focus is on improving the calculating efficiency. In this approach, each ship is assumed to be in each other’s far-field, and the near-field term in this Green function is neglected if the source point falls on one ship and the field point on others. Further, a matching relationship between the far-field waves and the interfered regions, which are defined as the overlapping areas between the mean wetted body surface of one ship and the propagating regions of the waves generated by another ship, is introduced to avoid the unnecessary computation of the relative terms of the Green function, if the field point is not in the overlapping areas. The approach is validated through studying the hydrodynamic terms and the free motions of two or three ships in side-by-side arrangement by comparing the obtained results with the model tests and the predictions of the exact method. The average calculating speed for the present approximate method is about 1.65-1.8 times of that for the exact method for solving the hydrodynamic interaction problem of two ships, and 2.56-2.73 times for that of three ships.

wave pattern, translating-pulsating source, calculation efficiency, model test, multiple ships

Introduction

Unlike the single ship case, the numerical simulation of the wave loads and the free motions of multiple ships advancing in waves is complex because the hydrodynamic interaction due to the presence of the other ships should be taken into account. Thus, each ship produces and scatters the radiation and diffraction waves which would excite other ships’ motions and interfere each other. Therefore, theoretically, the solution to this problem is to determine the wave loads excited by these complex waves around these ships. The patterns of the radiation-diffraction waves generated by a ship with forward and oscillatory motions, are known to change drastically and dependent on the value ofτ(whereτ=Uωe/g,Uis the forward speed,eωis the oscillating frequency, andgis the gravity acceleration)[1]. There are three wave patterns, that is, the ring wave pattern, the inner V and outer V wave pattern for 0τ＜＜0.25, and the ring-fan wave pattern. The fan wave pattern and the inner V wave pattern exist in the total waves forτ＞0.25 (see Fig.1). Except for the ring wave, other waves have a cusp, and the cusp angle is a function ofτ[1].rθ,fθ,oθandiθare defined as the the cusp angles of the ringfan wave, the fan wave, the outer V wave and the inner V wave, respectively. The method for calculating these cusp angles can be found in Ref.[1].

The 3-D surface panel method is usually applied to solve the seakeeping problem for ships with forward and oscillatory motions in waves[2-5]. With the linearized and the potential flow assumptions, the velocity potential of the radiation and diffraction waves generated by a ship can be constructed by means of the 3-D translating-pulsating source Green function for solving the boundary integral equation. This Green function satisfies the classical linearised free surface condition, and represents the velocity potential induced by a per unit strength source travelingat a forward speedUand oscillating at a frequencyeω. So it serves as a basic tool to describe the radiation and diffraction wave potentials in the present study. However, it is usually time consuming when applying this Green function in practice because the integrands of this function are oscillatory with high frequency[6,7], and very small integration steps are required to obtain a desired accuracy. In addition, a great number of panels are required to capture the important influence of the drastic waves especially for short waves e.g., the inner V waves for large values ofτ[1]. Therefore, it may be more time consuming in dealing with the present problem because the total number of the panel elements for multiple ships is much larger than that of a single ship. Many numerical techniques, such as the fast integration method for calculating the Green function[8,9], the analytical quadrature of the Green function over a panel or a segment[10], and the spline panel element method[11,12], were proposed to improve the calculation efficiency.

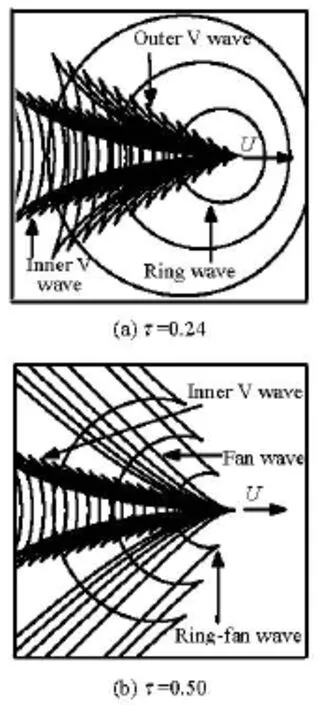
Fig.1 Definition of the diffraction-radiation wave patterns

In this paper, another method based on the 3-D surface panel method with the Havelock form Green function is proposed, which is characterized by the improvement in the calculating efficiency. A main feature of the approach is the neglect of the local flow component in the expression for the Green function in the computation of the influence coefficients associated with the interaction between the ship hulls. The numerical results demonstrate that this far field approximation is well justified, with a significant computational saving.

1. Mathematical formulas

1.1Velocity potentials

To analyze the hydrodynamic interaction for two ships, an earth-fixed system -OXYZand two body coordinate systemsoa-xayazafor ship-a andob-xbybzbfor ship-b are established, as shown in Fig.2. The origin of each system is placed on the undisturbed free surface, and thex-axis is positive in the direction of the speedU.xDandyDare defined as longitudinal and transverse distances between the two ships, respectively.

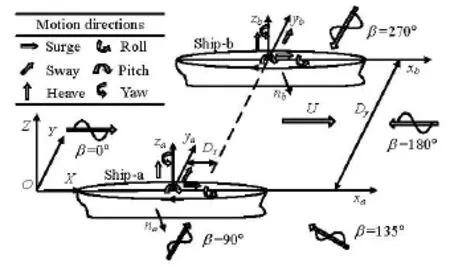
Fig.2 Coordinate systems

The fluid is assumed to be ideal and incompressible with a constant densityρ. The flow is assumed irrotational throughout, with surface tension effects neglected. The water depth is infinite. The two ships are assumed rigid and each of them oscillates in six degrees of freedom about their mean positions in regular waves. The incident wave amplitudeζis assumed to be small so that unsteady motions of these two ships are sinusoidal in time with the encounter frequencyeω. Then an unsteady potentialΦdue to incident waves, diffraction and radiation waves can be introduced

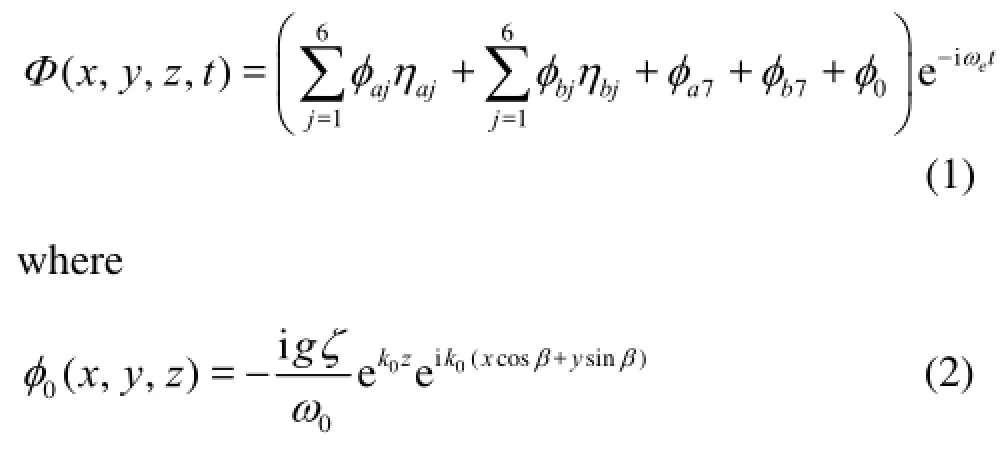
in which0φis the incident wave potential,0ω,0kandβare the frequency, the wave number and the incidental angle of the incident wave,ajφis the radiated wave potential due to the per unit amplitude motion inthe thjmode of ship-a while oscillations of ship-b is fixed,bjφis that of ship-b while oscillations of ship-a are fixed,ajη,bjηare the complex amplitudes in the thjmode motion of ship-a and ship-b, where the cases =1,2,6j… correspond to surge, sway, heave, roll, pitch and yaw, respectively, and7aφ,7bφare the diffraction potentials due to ship-a and ship-b, respectively.

1.2Boundary conditions

With the basic linear assumption, these diffraction and the radiation wave potentials must satisfy the Laplace’s equation in the fluid domain together with the boundary conditions on the free surface and the bottom, and the radiation condition in the far field. In addition, these potentials should satisfy the body boundary conditions on the mean wetted body surfacesaSandbS

where (na1,na2,na3)=na, (nb1,nb2,nb3)=nb, (na4,na5,na6)=ra×na, (nb4,nb5,nb6)=rb×nb,naandnbare the unit normal vectors outward to the mean wetted surfaces of the two ships,arandbrare the position vectors of a field point on the mean wetted surfaces pointing to the gravity center of ship-a and ship-b. Terms ofmaiandmbjare defined as follows:mai= 0 andmbj=0 forj=1-4,ma5=Una3,ma6=Una2,mb5=Unb3andmb6=-Unb2. Equations (4) shows that the two diffraction potential7aφand7bφcan be considered as a whole, which is defined as7φ.

2. Numerical implementation

2.1Boundary element integral equation

The solution of the above potentials can be constructed by means of the 3-D translating-pulsating source Green function for the boundary integral equation, which is formed by the surface integral over the mean wetted body surfaces and the free-surface contour integral along the intersection curvesaCandbCbetween the body surfaces and the undisturbed free surface

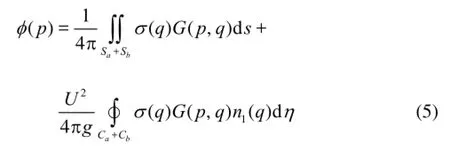
whereφcan be replaced byφaj,φbjandφ7.G(p,q) is the translating-pulsating source Green function at the field pointp(x,y,z) due to a source of unknown strengthσ(q) at the source pointq(ξ,η,ζ). This Green function can be expressed as Eq.(6) in so called Havelock form

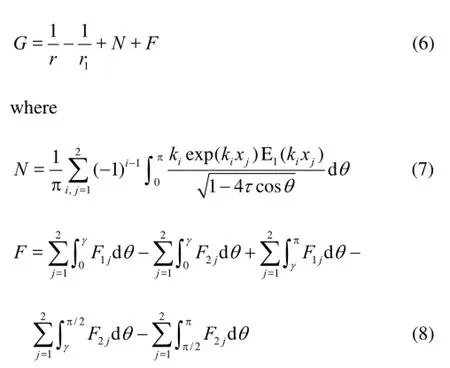
where 1/ris the Rankine source and 11/ris its image about the mean free surface.NandFare defined as the near-field component and the wave component of the Green function.1E is the exponential integral function. The five integral expressions ofFare defined as15-FF, respectively, and their integrandsijFare given as

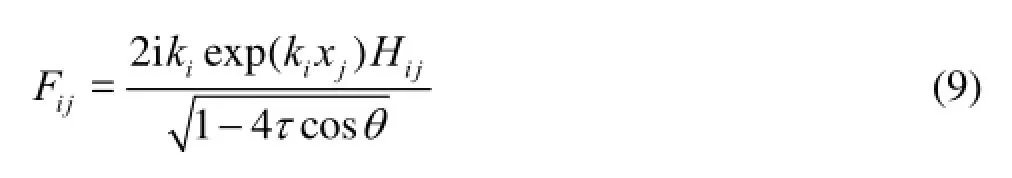
whereijHare defined as the control factors and their expressions can be found in Ref.[9]. The other parameters in Eq.(9) are defined by

By the method of Hess and Smith, the mean wetted body surfaces of these two ships can be discreted as a series of quadrilateral surface panels. Assuming that the source strength on each panel is equivalent and the control point (field point) is located at the centroid of the panel, then Eq.(10) can be discretized as

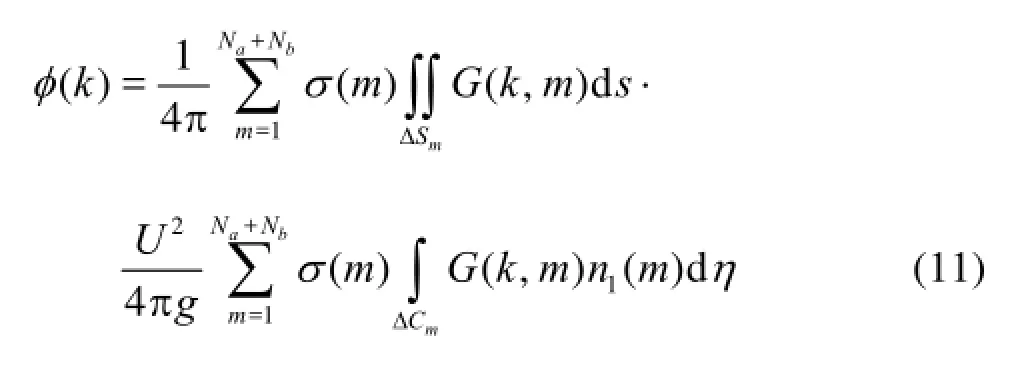
whereaN,bNare the total numbers of panels for ship-a and ship-b,mSΔ,mCΔ stand for the thmsurface panel and the waterline segment. It should be mentioned that when any side of the surface panel is not along the waterlines, the term about the waterline segment disappears, which otherwise should be considered. The method for calculating the waterline integral term can be found in Ref.[13]. Equation (11) can then be expressed in a matrix form as

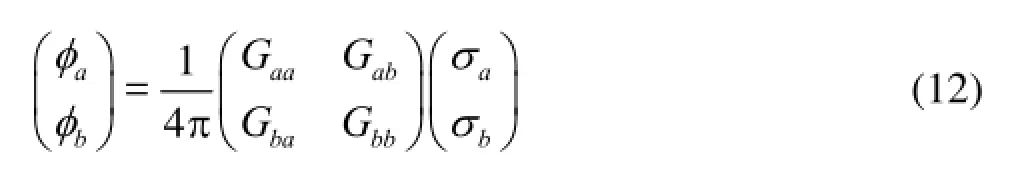
whereaaGis the influence submatrices of the Green

function when both the field point and the surface panel fall on ship-a,Gbbis that when both the field point and the surface panel fall on ship-b,Gabis that when the field point falls on ship-a and the surface panel is on ship-b, andGbais that when the field point falls on ship-b and the panel is on ship-a. Similarly, Eqs.(10) can be discretized as

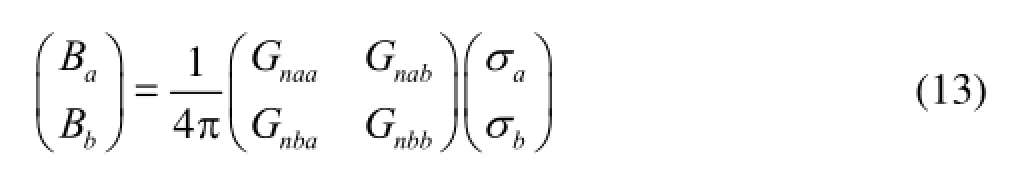
wherenaaG,nbbG,nabGandnbaGare the influence submatrices for the Green function gradient, for calculating the integrals of the partial derivatives of this Green function over the surface panels. Details of these partial derivatives together with their numerical calculation method can be found in Ref.[9].aBandBbare the body surface conditions on ship-a and shipb, whose values depend on the problem considered. The calculation of these influence matrices is the most important yet time-consuming step in the 3-D surface panel method. In this paper, an approximate method based on the performances of the Green function is proposed to improve the calculating efficiency, which is now explained as follows.

2.2Simplifying the calculation of the influence matrices

For large values ofX2+Y2, the exponential integral function can be expressed in the form

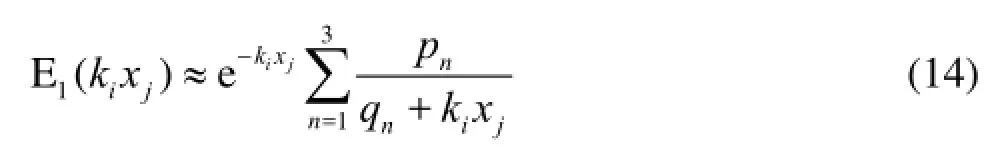
where1=p0.711903,2=p0.278518,3=p0.010389,1=q0.415775,2=q2.29428,3=q6.29000. Lettingqn+kixj=an+ibn(wherean,bnare real numbers), whenX2+Y2→∞, the termbn→∞, we obtain

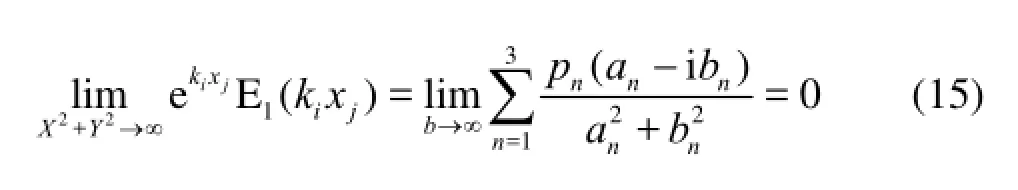
Equation (15) suggests that the contribution of the termNis not dominant as the distance between the source point and the field point is large. Therefore, the two ships can be considered to be in each other’s farfield, and the near-field component in the influence submatricesabG,baG,nabG,nbaGcan be neglected.

Now the focus turns to identify the interfered regions and the matching relationship between these regions and the wave patterns. By applying the stationary phase analysis to the phase functionsijψ, the wavepatterns for15-FFcan be obtained, and the details of this analysis can be found in Ref.[14]. For 0τ＜＜0.25,1Fand2Fare zero, and35-FFcorrespond, respectively, to the ring wave, the outer V and the inner V wave patterns. Forτ＞0.25, (F1+F4), (F2+F3) and correspond, respectively, to the fan wave, the fan-ring wave and the inner V wave patterns. Figure 3 shows the contourlines of the total potential together with its components for =τ0.5 on the free surface with the source located at (0,0,1)-. The distribution of the potentials on the free surface is consistent with the wave patterns shown in Fig.1(b).

Fig.3 Decomposition of the potential induced by the source

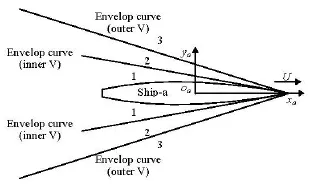
Fig.4 Decomposition of the propagating region for 0τ＜＜0.25

Figure 1 shows that the propagating region of each wave pattern can be determined at certain value ofτ. Taking ship-a for example, when 0＜τ＜0.25, the ring waves produced by this ship spread in all directions of the free surface, but the inner V and outer V wave patterns are confined to two wedge regions, respectively. Therefore, the propagating region of the total wave produced by ship-a can be divided into three regions which are denoted as 1-3 and depicted in Fig.4. As shown in this figure, all three type waves can propagate in area 1, the ring waves and outer V waves can spread in area 2, and only the ring wave can spread in area 3. The dividing lines between areas 1 and 2 are the pair envelop curves of the inner V wave, and those between areas 2 and 3 are the envelop curves of the outer V wave pattern. These two pair dividing lines can be expressed in the form of Eqs.(16) in the coordinate systemsoa-xayazaas

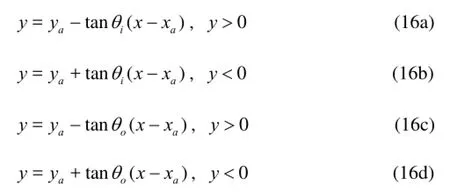
whereax,ayare the coordinates of the endpoint of the ship bow. Similarly, a decomposition can be made whenτ＞0.25 as shown in Fig.5. It should be pointed out that whenτ＞1.38, the positions of the dividing lines for the fan wave pattern and those for the inner V pattern should be exchanged because the cusp anglefθis smaller thaniθat this condition. By this decomposition, it would be easy to determine on which type area among those depicted in Fig.4 or Fig.5 each of the panel elements of ship-b falls, and the relative terms about the wave component of the Green function together with their partial derivatives can be chosen to match these areas, as given in Table 1. The match relationship shown in Table 1 is useful in determing whether each surface panel of ship-b is interfered or not by each wave pattern generated by ship-a, to avoid unnecessary computation for the non-interfered panel elements so as to improve the calculation efficiency. For ship-b, similar match relationship can be also obtained.

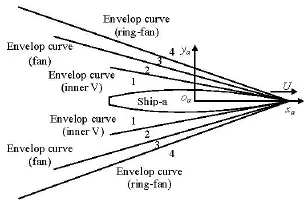
Fig.5 Decomposition of the propagating region for 0.25τ＜＜1.38

Table 1 Relationship between15-FFand propagating regions

2.3Hydrodynamic wave loads

The hydrodynamic pressure amplitude at any point on the mean wetted body surface of each ship can be obtained by using the potentials in the linearized Bernoulli’s equation

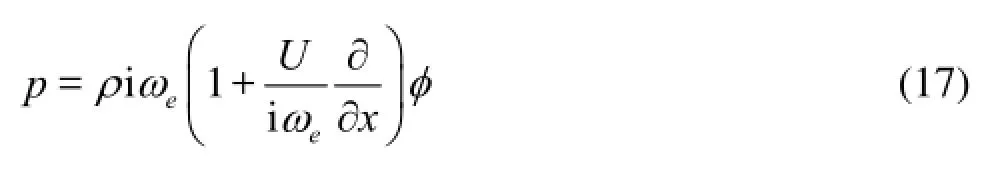
By taking the potentialφas the incident wave potential, the diffraction wave potential and the radiation potentials, the corresponding hydrodynamic pressure can be obtained. Then, the relative wave load can be obtained by integrating the relative pressure over the mean wetted surface of each ship

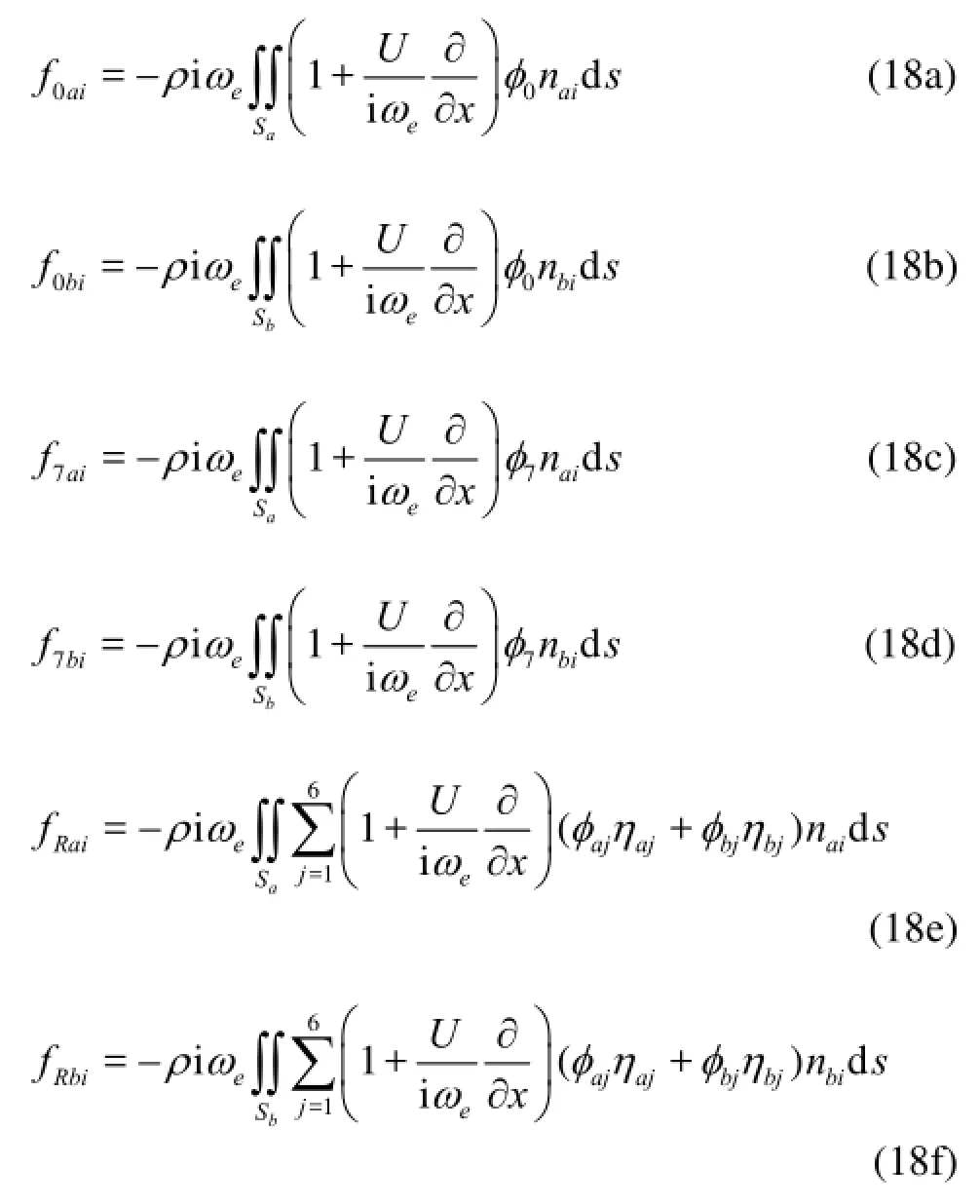
where0aif,7aifandRaifcorrespond to the amplitudes of the thidirection incident wave load, the diffraction wave load and the radiation wave load acting on ship-a, and0bif,7bifandRbifare those acting on ship-b.

2.4Free motions

Based on the rigid body dynamics, the coupled motions in the frequency domain for the two ships can be obtained as

whereaijMandbijMare the elements of the generalized mass matrices for the two ships.aijCandbijCare the elements of 6×6 restoring force coefficient matrices of the two ships. Details of expressions of the mass matrix and the restoring force coefficient matrix can be found in Ref.[15]. The complex amplitudes of motionsajηandbjηcan be obtained by solving these equations.

Fig.6 3-D Profiles and mesh arrangement of the two models

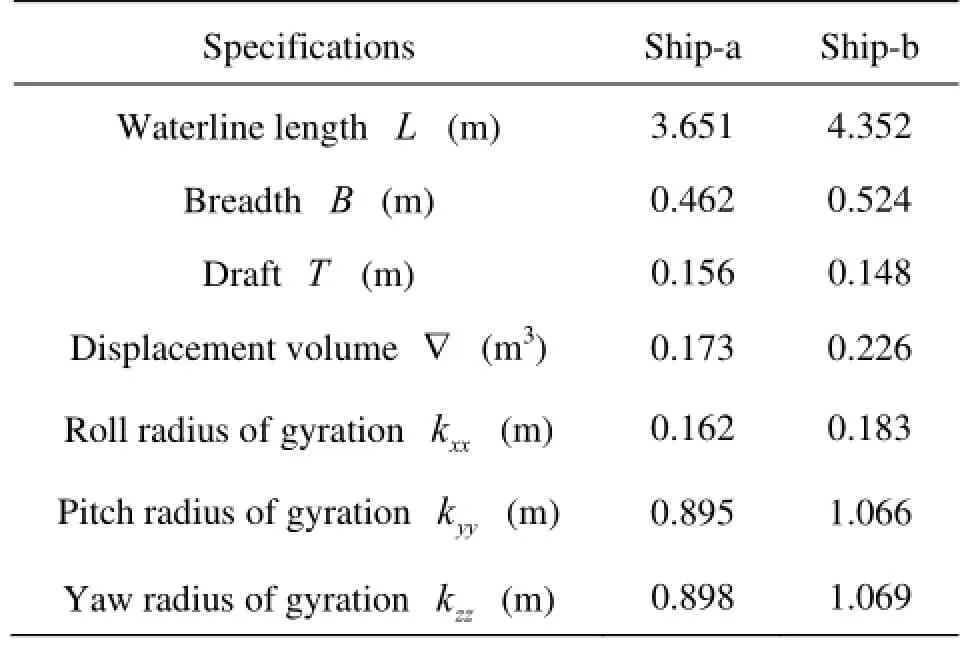
Table 2 The main particulars of the tested models

3. Validations and discussions

3.1Experiments

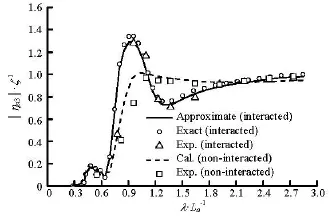
Fig.7 Amplitude of heave response of ship-a

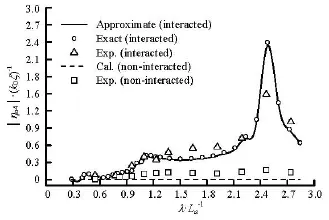
Fig.8 Amplitude of roll response of ship-a

3.2Comparisons with the experiments

The non-dimensinalized amplitudes of the heave, pitch and roll motions of ship-a measured in the experiment are shown in Fig.7-Fig.9. Figure 10 shows the non-dimensinalized heave motion amplitudes of shipb. The calculated results based on the present approximate method and the method without approximation (the exact method) are also shown in these figures. The heave amplitude is non-dimensionalized by the measured wave amplitudeζ, and the roll and pitch amplitudes are non-dimensionalized by the wave slope0kζ. As shown in these figures, the predictions of the present method and the exact method are in good agreement with the experiments. Details of the hydrodynamic interaction effects on the wave loads and the free motions can be captured by both methods. There are almost no discrepancies between these two predictions. The greatest discrepancies between experiments and predictions occur at the peak values of the roll motions in long wavelengths (see Fig.8). Under these conditions, the roll motions have large amplitudes, violating the linearity assumptions of the present prediction, which can be corrected by adding the roll viscous damping coefficients to the free motion equations.

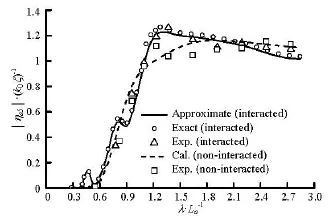
Fig.9 Amplitude of pitch response of ship-a

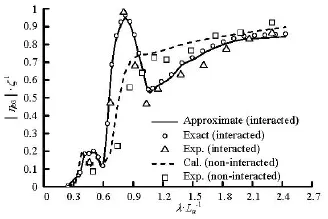
Fig.10 Amplitude of heave response of ship-b

3.3Discussions for the hydrodynamic pressure

The hydrodynamic pressure distributed on the body surface as a microscopic quantity, can be used to observe the local details of the hydrodynamic interaction effects on the two ships. Figure 11 shows the radiation pressure distribution on ship-b when the oscillations of ship-a are free and ship-b is fixed withFr=0.171,Dx=0,Dy=0.35La,τ=0.61 andβ= 180o.

It can be found from these figures that: (1) thepressure distributions obtained in these two methods are consistent with each other, which indicates that the local characteristics of the hydrodynamic interference can be captured by the the approximate method, (2) the pressure gradient distribution on ship-b indicates that in a part of area both the pressure gradient and the pressure amplitude tend to zero, but not in the remained area. The pressure distribution on the body surface is divided into two areas and an obvious dividing curve can be found. In the front region of the dividing line, the pressure amplitude almost approaches to zero, which means that this region is not excited by the radiation waves scattered from ship-a, but the pressure amplitude in the remained region is not zero. The region where the pressure amplitude tends to zero, is the non-interfered area. The other region, otherwise, is the interfered one. All the above shows that the division of interference on the wetted body surface is reasonable.

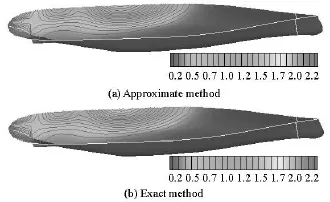
Fig.11 Amplitudes of the radiation hydrodynamic pressure distributed on ship-b with =β180o

3.4Application in the case of 3 ships

In this section, the approximate method presented above is generalized to deal with the hydrodynamic interaction of three ships advancing on a parallel course in waves. These three ships are, respectively, referred as ship-a, ship-b and ship-c. The unsteady potentialΦin the field can be written as

whereciφis the radiated wave potential due to the per unit amplitude motion in the thjmode of ship-c, andciηis the complex amplitude in the thjmode motion of this ship. The boundary conditions for these potentials are similar to those in the case of two ships presented above. By the method of Hess-Smith, these potentials on each body surface can be determined by the following two matrix form equations

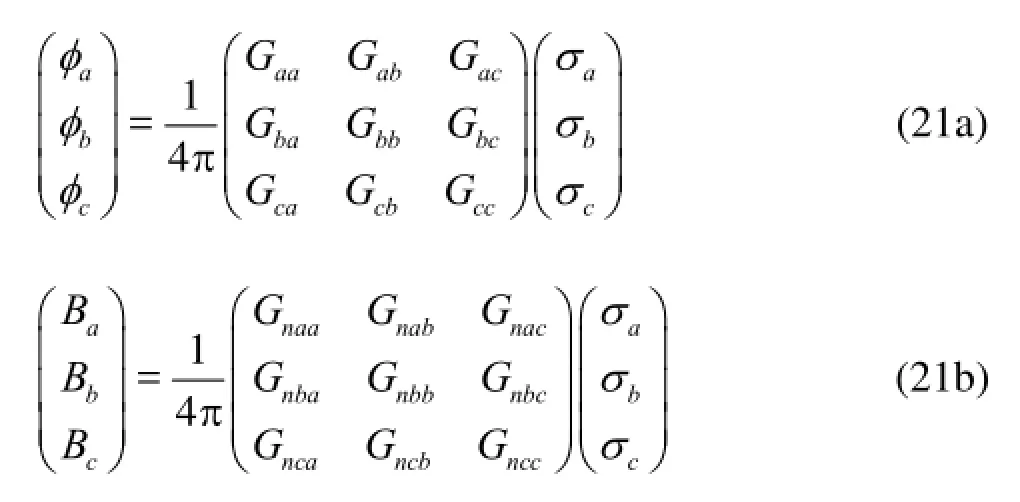
Except for the diagonal submatricesllGandnllG(where =,,labc) presented in Eqs.(21), the other submatrices of the influence matrices can be calculated by using the present approximate method. Once these matrices are obtained, the corresponding source strength and potentials can also be determined. The wave loads acting on each ship can be obtained by using the hydrodynamic pressure integration over each ship, and an 18 degree of freedom dynamic solver for the three ships can be developed.

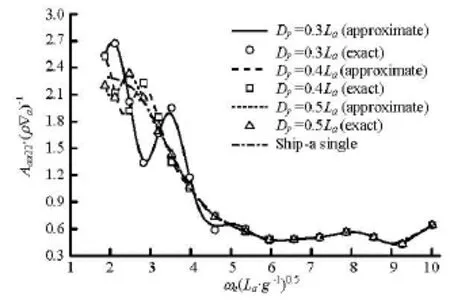
Fig.12 Sway added mass of ship-a due to its sway

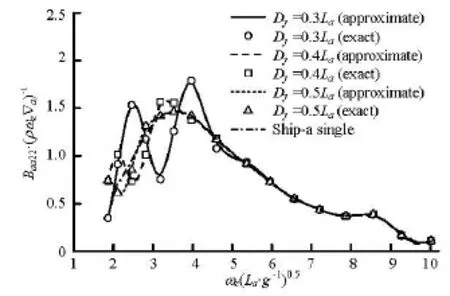
Fig.13 Sway damping of ship-a due to its sway

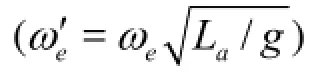
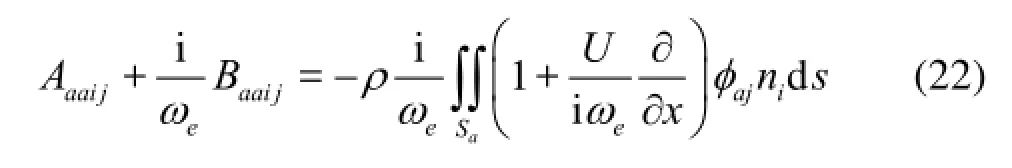
As shown in these figures, the hydrodynamic interference effects are significant in the low frequency range especially for cases of narrow separation, but are not significant in the high frequency range. These effects come from the excitation of the radiation waves produced by ship-a, which spread to ship-b and ship-c, then are reflected back to ship-a. For each separation distance, there exists a certain critical frequency for the hydrodynamic terms when the other ships are present. If frequencies are larger than this critical value, the interference effects on ship-a due to the other two ships disappear. In general, the dimensionless critical frequencies for the three separation distanceDy=0.3La, 0.4La, 0.5Laare about 5.3, 3.5 and 2.9, respectively. Besides, each curve of the interfered hydrodynamic term is in a fluctuation condition encircling the corresponding curve without interferences, and the fluctuation amplitude decreases with the growth of the separation distance, which means that the magnitude of the interacting effects on these hydrodynamic terms decreases with the growth of the separation distance.

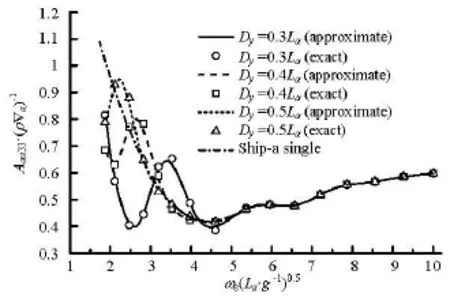
Fig.14 Heave added mass of ship-a due to its heave

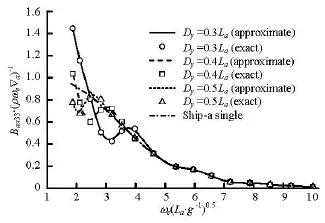
Fig.15 Heave damping of ship-a due to its heave

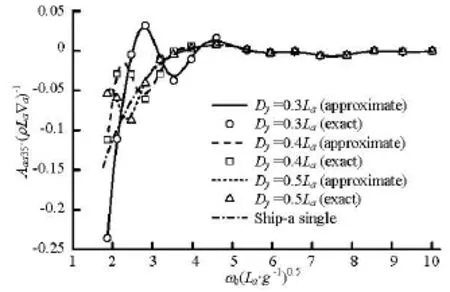
Fig.16 Heave-pitch added mass of ship-a due to its pitch

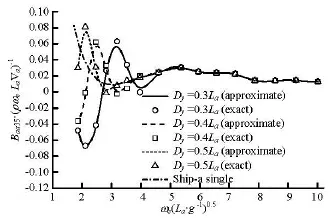
Fig.17 Heave-pitch damping of ship-a due to its pitch

4. CPU time analysis

The CPU time used in both methods to calculate the influence matrices for the pair models presented in Fig.6 with different separations is recorded at =Fr0.171 for values ofτranging from 0.1 to 3. Figure 18 shows the CPU time bit, which is defined as the ratio of the CPU time used for the approximate method to that for the exact method, withDy=0.35La, 0.5La, 0.65Laand 0.8La. With the increase ofτ, the CPU

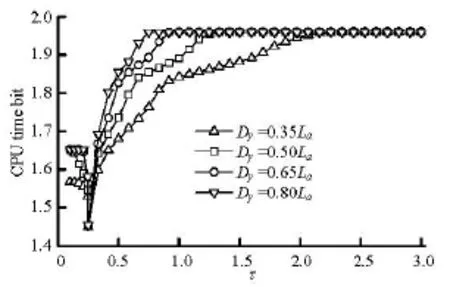
Fig.18 CPU time bit for calculating the influence matrices of two ships with differentyD

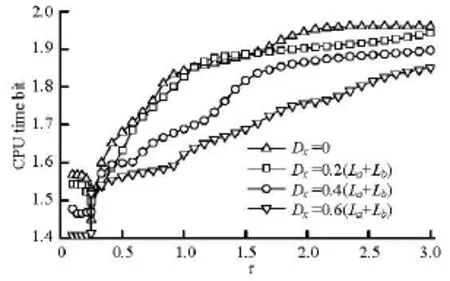
Fig.19 CPU time bit for calculating the influence matrices of two ships with differentxD

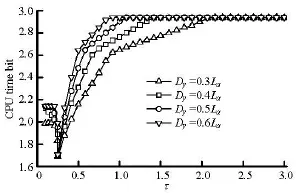
Fig.20 CPU time bit for calculating the influence matrices of three ships with differentyD

time bit of each curve first decreases and reaches a minimum value atτ≈0.25, then increases to a maximum value , and finally trends to a constant value (the maximum value). The minimum and maximum values are about 1.45 and 1.96, respectively. A critical value ofτcan also be found for each separation distance. Ifτis larger than this critical value, the hydrodynamic interactions between these two ships disappear. The critical value ofτis about 0.75, 1, 1.3 and 2.2 whenDyis equal to 0.8La, 0.65La, 0.5Laand 0.35La, respectively. The average calculating speed bit in these two methods for eachyD, respectively, is equal to 1.8, 1.84, 1.86 and 1.87 whenyDis 0.35aL, 0.5aL, 0.65aLand 0.8aL. These values reveal the improvement of the calculating efficiency through the use of the present method. Figure 19 shows each curve of the CPU time bit for the pair models withDx=0, 0.2(La+Lb), 0.4(La+Lb) and 0.6(La+Lb) whenDymaintains at 0.35La. The trend of each curve is similar to that presented in Fig.18, but no critical value ofτcan be found ifDx≠0. The average calculating speed for the present method is about 1.65, 1.73, 1.78 and 1.8 times of that for the exact method.

The statistical CPU time bits for the three Wigely hulls with different transverse separations are shown in Fig.20 at =Fr0.2 for 0.13τ＜＜. The trend of each curve is also similar to that presented in Fig.18, but the maximum and minimum values of the bit is about 2.92 and 1.72, respectively. The average calculating speed for the present method is about 2.56, 2.66, 2.71 and 2.73 times of that for the exact method. Therefore, the present method for solving the hydrodynamic interacting problem of three ships is more efficient than that of two ships.

5. Conclusions

The predictions of the wave loads and the free motions of two interacting ship models obtained by the approximate method show a satisfactory agreement with the experiments, and the accuracy is almost the same as that obtained by the exact method. This method can also be applied to solve the interaction problem of three ships advancing in waves.

The calculating efficiency to compute the influence matrices for the present method is better than that for the exact method, especially for larger values ofτor large transverse separations between ships. The average calculating speed for the present method is about 1.65-1.8 times of that for the exact method for the tested two ships, and 2.56-2.73 times for the tested three ships.

The wave patterns and the valid interfered regions can be adaptively matched by the relationship tables presented in this paper. This method is not at variance with the other improvement methods such as the fast integration method for calculating the Green function, the analytical quadrature of the Green function over a panel or a segment and the spline panel element method, thus it may be more efficient if it is combined with these methods to solve the present problem.

In addition, this approximate method can also be applied to improve the calculating efficiency for solving the seakeeping problem of a multihull ship adva-ncing in waves when using this 3-D Green function method.

[1] NOBLESSE F., HENDRIX D. On the theory of potential flow about a ship advancing in waves[J].Journal of Ship Research,1992, 36(1): 17-29

[2] DU S. X., HUDSON D. A. and PRICE W. G. et al. Prediction of three-dimensional seakeeping characteristics of fast hull forms: Influence of the line integral terms[C].25th International Conference on Fast Sea Transportation.Petersburg, Russia, 2005, 27-30.

[3] INOUE Y., KAMRUZZAMAN M. Analysis of hydrodynamic characteristics for arbitrary multihull ships advancing in waves[J].Journal of Marine Science and Technology,2008, 13(3): 231-243.

[4] ZAKARIA N. M. G. Effect of ship size, forward speed and wave direction on relative wave height of container ships in rough seas[J].Journal of the Institution of Engineers,2009, 72(3): 21-34.

[5] ZONG Zhi, QIN Kun. A three-dimensional moving and pulsating source (MAPS) method for calculating motions of trimaran hull forms[J].Journal of Ship Mechanics,2012, 16(11): 1239-1247(in Chinese).

[6] CHEN X. B. Highly oscillatory properties of unsteady ship waves[J].Journal of Mechanical Engineering,2000, 214(6): 813-823.

[7] NOBLESSE F., YANG C. Practical free surface Green functions for wave diffraction-radiation with forward speed[C].Proceedings of the 8th International Conference on Numerical Ship Hydrodynamics.Busan, Korea, 2003, 46-58.

[8] QIAN Kun. Study on calculation of motions and loads on floating bodies in large amplitude waves[D]. Doctoral Thesis, Dalian, China: Dalian university of Technology, 2004(in Chinese).

[9] XU Yong, DONG Wen-cai. Study on characteristics of 3-D translating-pulsating source Green function of deep-water Havelock form and its fast integration method[J].China Ocean Engineering,2011, 3(25): 365-380.

[10] MAURY C., DELHOMMEAU G. and BA M. et al. Comparison between numerical computations and experiment for seakeeping on ship models with forward speed[J].Journal of Ship Research,2003, 47(4): 347-364.

[11] BEENA V. I., SUBRAMANIAN V. A. Parametric studies on seaworthiness of SWATH ships[J].Ocean Engineering,2003, 30(9): 1077-1106.

[12] WANG Ke, ZHANG Xi and ZHANG Zhi-qiang et al. Numerical analysis of added mass and damping of floating production, storage and offloading system[J].Acta Mechanica Sinica,2012, 28(3): 870-876.

[13] DU S. X., HUDSON D. A. and PRICE W. G. et al. An investigation into irregular frequencies in hydrodynamic analysis of vessels with a zero or forward speed[J].Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment,2012, 226(2): 83-102.

[14] XU Yong. Study on the mechanism of hydrodynamic interaction between multiple ships advancing in waves at close proximity[D]. Doctoral Thesis, Wuhan, China: Naval University of Engineering, 2012(in Chinese).

[15] DAI Yi-shan, DUAN Wen-yang.Potential flow theory of ship motions in waves[M]. Beijing, China: National Defense Industry Press, 2008(in Chinese).

[16] JONCQUEZ S. A., ANDERSEN P. and BINGHAM H. B. A. Comparison of methods for computing the added resistance[J].Journal of Ship Research,2012, 56(2): 106-119.

10.1016/S1001-6058(13)60433-3

* Project supported by the National Natural Science Foundation of China (Grant No. 50879090), the Key Research Program of Hydrodynamics of China (Grant No. 9140A14030712JB11044).

Biography: XU Yong (1981-), Male, Ph. D., Engineer