Finite element analysis of second order wave radiation by a group of cylinders in the time domain*

WANG Chi-zhong (王赤忠)

Department of Ocean Science and Engineering, Zhejiang University, Hangzhou 310058, China

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore, E-mail: cz_wang@zju.edu.cn

MITRA Santanu

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore

HUANG Hao-cai (黄豪彩)

Department of Ocean Science and Engineering, Zhejiang University, Hangzhou 310058, China

KHOO Boo-cheong

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore

Finite element analysis of second order wave radiation by a group of cylinders in the time domain*

WANG Chi-zhong (王赤忠)

Department of Ocean Science and Engineering, Zhejiang University, Hangzhou 310058, China

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore, E-mail: cz_wang@zju.edu.cn

MITRA Santanu

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore

HUANG Hao-cai (黄豪彩)

Department of Ocean Science and Engineering, Zhejiang University, Hangzhou 310058, China

KHOO Boo-cheong

Department of Mechanical Engineering, National University of Singapore, Singapore 119260, Singapore

(Received May 11, 2012, Revised June 26, 2012)

A finite element based numerical method is employed to analyze the wave radiation by multiple or a group of cylinders in the time domain. The nonlinear free surface and body surface boundary conditions are satisfied based on the perturbation method up to the second order. The first- and second-order velocity potential problems at each time step are solved through a Finite Element Method (FEM). The matrix equation of the FEM is solved through iteration and the initial solution is obtained from the result at the previous time step. The three-dimensional (3-D) mesh required is generated based on a two-dimensional (2-D) hybrid mesh on a horizontal plane and its extension in the vertical direction. The hybrid mesh is generated by combining an unstructured grid away from cylinders and two structured grids near the cylinder and the artificial boundary. The fluid velocity on the free surface and the cylinder surface are calculated by using a differential method. Results for various configurations including the cases of two cylinders and four cylinders and a group of eighteen cylinders are obtained to show the joint influences of cylinders on the first- and secondorder waves and forces, including the effects of spacing ratios and wave frequency on the second order waves and the mean force, in particular.

second order wave radiation, time domain, a group of cylinders, finite element method, unstructured mesh

Introduction

With the development of oil exploration and production in deep water, the design of offshore structures such as Tension Leg Platforms (TLPs), semi-submersibles and drilling ships become interesting topics and are extensively studied. The TLP is the most common offshore structure for deep-water operations. It mainly consists of a few columns and tendons for constraining the motion of the platform, and so the interactions between the waves and the structures of multiple bodies are very important research issues. The perturbation method is a powerful tool to predict the hydrodynamic forces and the motions of offshore structures. There are many studies of wave-body interactions based on the perturbation method since the work of Lighthill and Molin in 1979. There are also many studies of the wave diffraction and radiation problems. Based on the linear wave theory, Maniar et al.[1]studied the linear diffraction by an array of 101 cylinders. They found that when the wave number was close to the trapped mode, very large hydrodynamic forces would be induced on the middle cylinders.Evans and Porter[2]also showed that a very large force could be induced on a small number of cylinders, such as four, especially when they were quite close to each other. The second order wave diffraction by multiple bodies were studied by Malenica et al.[3]in the frequency domain and Wang and Wu[4]in the time domain. Newman[5]discussed the wave effects on multiple bodies of different shapes.

It is known from the studies mentioned-above that the wave interference by multiple bodies would happen and may cause a large wave and hydrodynamic force on some bodies due to the wave diffraction. Some similar phenomena may happen due to the wave radiation by multiple bodies. The waves produced by the motions of multiple bodies will interact with each other. The wave radiation by multiple bodies has many applications in ship and ocean engineering problems such as for TLPs, semi-submersibles, floating airports and some special ships such as catamaran and Small Waterplane Area Twin Hull ship (SWATH) that have two hulls and the interference may be important while advancing in waves. In addition, two or more vessels in sufficient proximity may have significant interactions. Wu and Hu[6]simulated the large amplitude motions of two vertical cylinders. Zhu el al.[7]studied the radiation problem of multiple structures with small gaps. Recently, Wang and Wu[8]studied the 2D wave radiation by two floating bodies in forced motions based on the time-domain second-order theory. Their numerical results show that the wave motion becomes very large and even infinite at the first- and second-order resonant frequencies, which is very similar to the sloshing in a tank[9]. Kashiwagi and Shi[10]obtained the pressure distribution by computations based on the wave-interaction theory for adjacent multiple bodies.

Most of studies mentioned above are based on the frequency domain method (for example, Zhu et al.[7]and Kashiwagi and Shi[10]). In the present paper, we employ a finite element numerical method to simulate the second order wave radiation by multiple truncated cylinders in the time domain based on unstructured meshes. Compared with the frequency domain method, the time domain method can be easily extended to irregular and random waves. The finite element method is a powerful and efficient numerical tool for simulating nonlinear water waves. The global coefficient matrix in the FEM is symmetric and sparse, which can be put efficiently into a packed storage of nonzero elements. Therefore, a smaller storage and less computational resources are required than the boundary element method, which requires a full matrix. In the present simulations, the linear and second order waves and hydrodynamic forces are obtained by the FEM and the wave interference between cylinders is investigated through changing the wave frequency and the spacing between cylinders. Two, four and eighteen cylinders are considered to show the mutual influence of waves and cylinders.

Fig.1 A sketch of the problem

1. Mathematical formulation

We consider the second order wave radiation by a group or an array of cylinders. As shown in Fig.1, a right-handed Cartesian coordinate systemoxyz is defined, in which x and y are in the horizontal plane and zpoints vertically upwards from the still water level. Thei -th cylinder surface is denoted by Sib(i=1, 2,…,n , where nis the number of cylinders) and its unit normal vector directed outward from the fluid region is denoted byNi=(Nix,Niy,Niz). The seabed is assumed horizontal along the planez=-h. Lettdenote the time andηthe elevation of the free surface Sfrelative to the still water level. When the fluid is assumed incompressible and inviscid, and the flow irrotational, the fluid motion can be described by a velocity potentialφwhich satisfies the Laplace equation within the fluid domain∀

and is subject to the following boundary conditions:

where g is the acceleration of gravity,Viis the translational oscillatory velocity of thei -th cylinder and Ωiis the rotational velocity about a point on the i-thcylinder, which may be chosen as the mass centre of the body and riis the position vector from a point on the i-th body surface to the mass centre. In addition, the potential satisfies the radiation condition imposed through a suitable numerical procedure applied on a control surfaceSclocated at some distance away from the body as shown in Fig.1.

One of the major difficulties in solving the above-mentioned fully nonlinear free surface potential flow problems is the treatment of the free surface boundary conditions (2) and (3), which are both nonlinear and defined on the free surface which is not known before the problem is solved. Here we will consider the problem up to the second order.

and is subject to the boundary conditions applied on the still water surface, the mean body surface and the seabed, given, respectively, as

where Xiand Θiare considered up to the first order only, and the matrixH˜is given as

For the first order solution, the problem corresponds to the linear wave radiation problem, for the second order solution, the boundary problem is inhomogeneous and f(2),f(2)and v(2)represent the quadratic

12i forcings of the corresponding free surface and body surface conditions which can be determined from the first order solution.

The second order hydrodynamic forces on the i-th body can be obtained by carrying out a direct integration of the pressure over the mean wetted body surface and the correction integral defined at the still waterlineWL. The hydrodynamic force contains three components

where F(1),F(2)and F(2)are the first order oscilla

iii tory force at the excitation frequency, the second order oscillatory force at twice the excitation frequency and the second order mean force, respectively.

Fig.2 A 3-D mesh for four truncated cylinders

2. Finite element discretization and numerical procedures

2.1 Finite element discretization

We use the finite element method here. A 2-D mesh generator called BAMG[11]is used to generate the unstructured 2-D grid on the plane first. It is then extended along the vertical direction to form the 3-D mesh of prismatic elements, as shown in Fig.2 for four truncated cylinders. The disturbance due the water waves usually decays very rapidly along the depth. It is, therefore, reasonable to use smaller elements near the free surface and larger elements near the bottom. The detailed description of the distribution of nodes on the boundary can be found in Ref.[12].

Once the mesh is generated, the potentials φ(k)(k=1,2)can be expressed in terms of the shape functionNJ(x, y, z)

where φ(k)is the potential at node Jandnis the J number of nodes. Based on the Galerkin method, we have

Using the Green’s identity and the boundary conditions, we can obtain the following matrix equations

where

where Sprepresents the Dirichlet boundary on which the potentials, denoted byf(k)(k=1,2), are known,p andSnrepresents the Neumann boundary on which the normal derivatives of the potentials, denoted by f(k)(k=1,2), are known. The matrix equations are n then solved through an iteration based on the conjugate gradient method with a Symmetric Successive Over-Relaxation (SSOR) pre-conditioner.

2.2 Update potential and wave elevation on free surface

The fourth order Adams-Bashforth scheme is used to advance the simulation through the time stepping method

where f( t)represents either the velocity potential or the wave elevation on the free surface. This scheme provides a high order accuracy and is particularly suitable for the solution based on the perturbation procedure. As the mesh is fixed and no remeshing is required throughout the process of the simulation, the information including the wave elevation, the potential and the velocity at the previous time steps can be stored easily.

Fig.3 The hybrid mesh on the free surface with a structured mesh near the cylinder and another structured mesh near the artificial boundary

2.3 Absorbing boundary conditions

For long time simulations, an appropriate radiation condition should be imposed on the boundary Scto minimize the wave reflection. Here we use a combination of the Sommerfeld-Orlanski condition and a damping zone. In order to use this condition, we use a structured mesh near the boundary Sc(see the structured Mesh 1 in Fig.3), the potential and the velocity on the node of the structured mesh can be calculated directly. Otherwise, an interpolation will be required at the expense of the accuracy. We rewrite Eq.(7) as

where νis the damping coefficient given by

wherer is the distance of the point under consideration to the centre of the nearest cylinder. For the single body shown in Fig.4, the damping zone starts from the edge of an inner rectangle r= r0( x, y)and ends at the outer rectangle r= r0( x, y) + Cw(x, y),Csis a constant to control the strength of the damping coefficient and is chosen to be 1.0 in this study, and the width of the damping zoneLdm(see Fig.4) is set to be one wavelength for short waves and eight times the radius of the cylinder for long waves.

Fig.4 Damping zone on the free surface

2.4 The evaluation of first- and second-order derivatives on the free surface and the body surface

After the potential is found, its first and second order derivatives on the element nodes are required to update η(k)and φ(k)through Eqs.(7) and (8). The derivatives can theoretically be obtained through the differentiation of the shape function. However, the accuracy is usually not good enough when the order of the shape function is low and the result becomes zero when the order of the derivative is higher than that of the shape function. Here we employ a cubic polynomial to express the velocity potential along the straight mesh line in the vertical direction

and its first- and second-order derivatives with respect to z (k=1,2)can be easily calculated, the following equation is then used to obtain the horizontal components and∂φ(k)/∂ y:

Fig.5 Histories of vertical forces at k0a=1.0

Fig.6 First order force versus k0a

Fig.7 Second order force components versus k0a

Fig.8 Total second order force and mean force versus k0a

Fig.9 Histories of second order waves for Cylinder 1 at k0a= 1.0

In the first- and second-order body surface condition Eq.(9), some derivatives such as ∂φ(1)/∂x,∂φ(1)/∂y,∂φ(1)/∂z,∂2φ(1)/∂x2,∂2φ(1)/∂y2,∂2φ(1)/∂z2,∂2φ(1)/∂x∂ y,∂2φ(1)/∂y∂ zand ∂2φ(1)/∂z∂ x, are required. We can use the differentiation to obtain these derivatives through interpolations. However, it may affect the accuracy. Thus, we use a hybrid mesh on the free surface, in which a structured mesh (the structured Mesh 2 in Fig.3) in a torus shaped region is used near each cylinder. The structured mesh is obtained through discretizing the torus by dividing it into some segments in the tangential directionτuniformly, clockwisely and with four segments in the normal directionn directed toward the cylinder.

Fig.10 Histories of waves for Cylinder 1 at k0a=1.0

Fig.11 Comparisons of linear and second order waves for Cylinder 1 at k0a=1.0

On the bottom of each cylinder, the calculations of all first- and second-order derivatives are conducted the same as those on the free surface.

On the wall of the cylinder, the first- and secondorder derivatives ∂φ/∂nand ∂2φ/∂n2along the normal direction ncan be calcu lated through a differentialmethod.Similarly,thetangentialderivatives

Fig.12 Comparisons of linear and second order forces at k0a= 1.0

Fig.13 Histories of hydrodynamic force on Cylinder 1 at k0a= 1.0

∂φ/ ∂τand ∂2φ/∂τ2may be obtained along the tangential directionτ. The derivative ∂2φ/∂n∂τcan be calculated by differencing∂φ/∂nalong the tangential direction after∂φ/∂nis obtained. All derivatives of the potential with respect tox,yandzcan be obtained through the following equations:

Fig.14 Linear and second order forces versus k0a

Fig.15 Comparison of first order forces

3. Numerical results

In the numerical simulation, the body is in a harmonic motions v. In order to let the wave develop gradually, we modifyvto be

where v′is the real motion and M( t )is defined as

and T=2π/ωis the wave period. The use of Eq.(23) helps the wave to approach the periodic state more smoothly and quickly.

3.1 Single cylinder cases

We first consider a single truncated cylinder in vertical motions to validate the present numerical method. The water depth is h=a , whereais the radius of the cross section of the cylinder and the height of the cylinder isd= h/2. The cylinder is subject to the following harmonic motion in the vertical direction

Fig.16 Comparisons of second order force and components

Fig.17 Linear and second order waves for Cylinder 1 versus spacing between two cylinders at k0a=1.0

3.2 Two-cylinder cases

We next consider the wave radiation by two identical cylinders in vertical motions given by Eq.(24). The dimension of each cylinder is the same as the above single cylinder. The spacing between the two cylinders is Lcy=4a. The centre of the cross section of each cylinder is on the liney=0, and Cylinders 1 and 2 are located at(-2a,0)and (2a,0), respectively. We consider Cylinder 1 only because of symmetry. The nondimensional wavenumber isk0a=1.0and the water depth h=a. The second order wave on the left and right sides of cylinder 1 are shown in Fig.9. It is seen that the development of the waves is very smooth and stable periodic states are reached within 20 cycles.

Fig.18 Linear and second forces on Cylinder 1 versus spacing between two cylinders at k0a=1.0

Fig.19 Wave profiles at t/T=19 (k0a =1.0and Lcy=5a) in vertical motions

Fig.20 Linear and second wave for Cylinder 1 at k0a=1.0

Fig.21 Wave profiles at t/ T =19(k0a =1.0and Lcy=4a) in horizontal motions in thex -direction

Fig.22 Histories of hydrodynamic forces on Cylinder 1 at k0a=1.0

The linear and the linear plus second order waves are shown in Fig.10 and the nonlinear feature can be clearly seen. A comparison of the linear and the second order waves between this two-cylinder case and a single isolated cylinder case by removing Cylinder 2 is shown in Fig.11. It is seen that the waves at the left side in the two cases are slightly different for the

Fig.23 Four-cylinder case

Fig.24 Histories of waves for Cylinder 1 at k0a=1.0

Fig.25 Histories of hydrodynamic force on Cylinder 1 at k0a= 1.0

linear wave but almost identical for the second order wave. However, both linear and second order waves at the right side are clearly different in both phase and amplitude. The comparison of the linear and second order forces in the vertical direction is shown in Fig.12. There is very small difference for the linearforce in both phase and amplitude, but the second order force in the two-cylinder case is bigger than that in the single cylinder case. Fig.13 shows the history of the hydrodynamic force. It is seen that the nonlinearity is clearly seen for the component in z -direction.

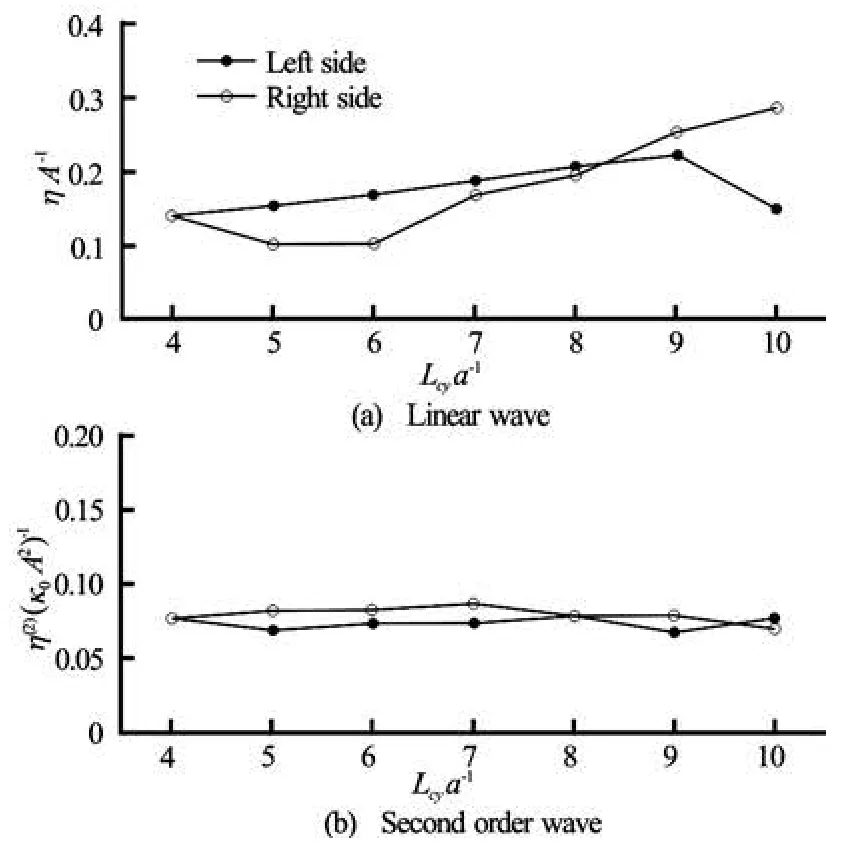
Fig.26 Linear and second order waves for Cylinder 1 versus spacing between both cylinders at k0a=1.0

The variations of the force and its components in x -and z-directions with the nondimensional wavenumberk0aand Lcy=5aare shown in Fig.14. The horizontal linear force increases withk0aand reaches its maximum at around k0a=2.13and then decreases. The vertical force, however, shows a converse trend withk0a. It is seen that the second order force in the vertical direction, its component due to the second order potential and the mean force have more complicate variations withk0a. The vertical force and its components are compared with those in the single cylinder case mentioned above and the results are shown in Figs.15 and 16. The difference between them is clearly seen, especially for the total second order force and the component due to the second order potential.

Figure 17 shows that the first and second order waves for Cylinder 1 varying with the spacing between two cylinders. It is seen that both the first and the second order waves at the left side change slowly with the spacing but those at the right side are more affected by the spacing. The maximum wave amplitude at the right side is much larger than that at the left side for both the linear and the second order waves. The corresponding force versus k0ais shown in Fig.18. Generally speaking, the effect of spacing on the vertical force and its components is small. In the horizontal direction, the spacing has an important influence on the second order force in the horizontal direction Fx(2)and the component Fx(22)due to the second order potential, and the influence on the second order mean forceis also clearly seen. Figure 19 shows the snapshot of the wave profile around the cylinders att/ T=19. The nonlinear feature of the wave can be observed from the figure.

Fig.27 Linear and second forces on Cylinder 1 versus spacing between both cylinders at k0a=1.0

Simulations are also carried out for two cylinders in swaying motions at k0a =1.0and A=0.1ain the same direction. Results for two cylinders at (-2a,0) and (2a,0), respectively, moving in x-direction given by Eq.(24) are shown in .Figs.(20)-(22). It is seen from Fig.20 that the nonlinearity of the wave at the right is very clearly seen and the second order effect of the wave on the whole free surface is also important (see Fig.21). The hydrodynamic force on Cylinder 1 is shown in Fig.22 and it can be seen that the second order component is not clearly seen inxdirection but very important in z-direction. It is known that the linear force component exists inx-direction only but the second order component inz-direction only for a symmetric floating body moving in thex-direction. Hence, the influence by the interference by Cylinders 2 and 1 is important.

Fig.28 Wave profiles at t/ T =19in horizontal motion

Fig.29 Eighteen-cylinder case

3.3 Four-cylinder cases

We discuss some four-cylinder cases in this section as shown in Fig.23. The water depth h=3aand the cylinder heightd= h/2. All cylinders are in vertical or horizontal motions described by Eq.(24). The configuration is symmetric about bothx -and yaxes and Cylinders 1 and 2 are located at (-2a,0)and (2a,2a), respectively. The nondimensional wavenumber isk0a =1.0and the oscillational amplitude A=0.1a. Firstly, a case of vertical motions is simulated. The waves on the left and right sides of Cylinder 1 are shown in Fig.24. It seems that the wave nonlinear feature is weak. The hydrodynamic force, however, has a stronger nonlinearity for both components inx -and z-directions as shown in Fig.25. Figure 26 shows the first and the second order waves for Cylinder 1 varying with the spacingLcy. The linear wave at the left side slowly increases withLcywhen Lcyis less than 9 but generally becomes larger when Lcyincreases for the wave at the right side. It seems that the second order waves slightly change with Lcyat both left and right sides. The corresponding force versus k0ais shown in Fig.27. The case of all four cylinders in identically horizontal motion as in above cases is also considered and Fig.28 shows the wave profiles att/ T=19. It can be seen that the effect of the second order wave is significant.

Fig.30 Histories of first and second order waves at the right side of Cylinders 1, 2 and 5 at k0a=0.5

Fig.31 Histories of waves at the right side of Cylinder 1, 2 and 5 at k0a=0.5

Fig.32 Histories of hydrodynamic force on Cylinder 1 at k0a=0.5

Fig.33 Histories of hydrodynamic force on Cylinder 5 at k0a=0.5

3.4 An array of cylinders cases

Finally, an array of eighteen cylinders in two lines in vertical motions is simulated (see Fig.29). The wave depth is h=3aand Lcy=8a. We consider cases atk0a=0.5. The wave at the right sides of Cylinders 1, 2 and 5 are shown in Figs.30 and 31. The linear wave amplitude for Cylinder 1 is larger than those for Cylinders 2 and 5 and that for Cylinder 5 is the smallest. The second order waves are, however, are almost identical. It is also seen that the wave for cylinder 5 has a stronger nonlinearity due to the smallest linear wave amplitude. The hydrodynamic forces on cylinder 1 and 5 are shown in Figs.32 and 33, respectively. The force in x-direction for Cylinder 1 is smaller but has a strong nonlinearity. It is seen that the force iny-direction for Cylinder 5 is larger than that for Cylinder 1. The nonlinear feature of the force inz-direction for Cylinder 1 is clearer seen than that for Cylinder 5 although there is little difference between their linear components. The wave profiles at t=30Tare shown in Fig.34. The second order wave effect is clearly seen.

Fig.34 Wave profiles at t/ T =30in vertical motion at A= 0.1a

4. Conclusions

A finite element based numerical method is employed to study the second order wave radiation by multiple truncated cylinders in open seas. The 3-D mesh is obtained through an extension of a 2-D hybrid mesh linked by a Delaunay unstructured grid and two structured grids near the cylinder and the truncated artificial boundary, respectively. The finite element method is employed to calculate the velocity potential in the fluid domain and the differential method is used to calculate the velocity on the free surface and the body surface.

Different configurations are numerically simulated. The wave runup and the first and the second order forces are calculated, which are of significance for the design of multi-body ocean structures such as the gap between the water surface and the platform deck and the drift motion of the platform.

Two-cylinder cases of vertical motions are studied. The steady state solutions are achieved over a long duration in terms of the first and second order waves. The amplitudes of the first and second forces vary with the spacing between two cylinders are discussed and comparisons are made with those in the single isolated cylinder cases. Results show that both the first and the second order waves in the region between two cylinders may be more affected by theinterference. For the horizontal force, the total second order force Fx(2)and the component Fx(22)may change quickly with the spacing. The vertical force and its components are, however, are generally slightly affected by the spacing.

Furthermore, some four-cylinder cases are also investigated. The first and the second order waves and the hydrodynamic forces are calculated and their variations with the cylinder spacing are also discussed. Finally, simulations of the wave radiation by an array of eighteen cylinders are carried out.

[1] MANIAR H. D., NEWMAN J. N. Wave diffraction by a long array of cylinders[J]. Journal of Fluid Mecha- nics, 1997, 339: 309-330.

[2] EVANS D. V., PORTER R. Trapped modes about multiple cylinders in a channel[J]. Journal of Fluid Me- chanics, 1997, 339: 331-356.

[3] MALENICA S., EATOCK TAYLOR R. and HUANG J. B. Second order water wave diffraction by an array of vertical cylinders[J]. Journal of Fluid Mechanics, 1999, 390: 349-373.

[4] WANG C. Z., WU G. X. Time domain analysis of second order wave diffraction by an array of vertical cylinders[J]. Journal of Fluids and Structures, 2007, 23(4): 605-631.

[5] NEWMAN J. N. Wave effects on multiple bodies[C]. The International Conference in Honor of Professor Ohkusu on the Occasion of his Retirement. Fukuoka, Janpan, 2001, 3-26.

[6] WU G. X., HU Z. Z. Simulation of nonlinear interactions between waves and floating bodies through a finite element based numerical tank[J]. Proceedings of the Royal Society London, Series A, 2004, 460(2050): 2797-2817.

[7] ZHU Ren-chuan, MIAO Guo-ping and ZHU Hai-rong. The Radiation problem of multiple structures with small gaps In between[J]. Journal of Hydrodynamics Ser. B, 2006, 18(5): 520-526.

[8] WANG C. Z., WU G. X. Analysis of second order resonance in wave interactions with floating bodies through a finite element method[J]. Ocean Engineering, 2008, 35(8-9): 717-726.

[9] WU G. X. Second order resonance of sloshing in a tank[J]. Ocean Engineering, 2007, 34(17-18): 2345-2349.

[10] KASHIWAGI M., SHI Qi-qi. Pressure distribution computed by wave-interaction theory for adjacent multiple bodies[J]. Journal of Hydrodynamics, 2010, 22(5Suppl.): 526-531.

[11] HECHT F. BAMG: Bidimensional anisotropic mesh generator[R]. Technical Report, Rocquencourt, France: INRIA, 2006.

[12] CHUNG T. J. Computational fluid dynamics[M]. Cambridge, UK: Cambridge University Press, 2002, 544.

[13] LI Y. Simulation of 3D nonlinear wave-structure interaction in a numerical wave basin[D]. Doctroral Thesis, Halifax, Canada: Technnical University of Nova Scotia Halifax, 1995.

[14] GOREN O. On the second-order wave radiation of an oscillating vertical circular in finite-depth water[J]. Journal of Ship Research, 1996, 40(3): 224-234.

10.1016/S1001-6058(11)60373-X

* Project supported by the Fundamental Research Funds for the Central Universities and NPRP 08-691-2-289 grant from Qatar National Research Fund (QNRF)

Biography: WANG Chi-zhong (1968-), Male, Ph. D., Associate Professor

HUANG Hao-cai, E-mail: hchuang@zju.edu.cn