无源二维交叉定位分析

2013-06-01张笑

电子科技 2013年2期

张笑

(西安电子科技大学电子工程学院，陕西西安 710071)

无源定位系统最大的优点在于工作时本身不发射电磁能量，所以具有良好的隐蔽性，能有效地抵抗反辐射导弹和反侦察定位系统，因此生命力强，适应环境快［1］。其次，无缘定位技术与收发分置的双基或多基雷达系统类似，且工作在甚高频和超高频，因此能更有效地对隐身目标进行探测定位。再次，无源雷达系统自身不发射信号，省去了昂贵的高功率发射机和收发开关及相关电子设备，使系统制造和维护成本大幅降低。最后，外辐射源的天线都设置在贴近地面的高处，因此对低空飞行的飞机和巡航导弹有利，具有良好的抗低空突防性能［2］。

1 二维交叉定位

测向交叉定位法(DOA)又称三角定位法，在二维或三维空间上经过射线交叉置，是无源定位中使用最多的一种定位方法［3］。

1.1 二维交叉定位算法

两条射线的交叉定位，使用两部雷达建立一条测量基线，如图1所示。设主基地雷达站O的坐标为(0，0)，可以测量雷达站A到O的距离L，以及A相对于O的方位角α。如图所示，M为目标辐射源所在位置，M(X，Y)为所求的坐标。其中a0和a1为雷达测向所探测的目标方位角。

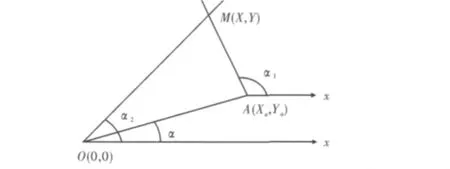
图1 二维测向交叉定位原理图

雷达站A的坐标为

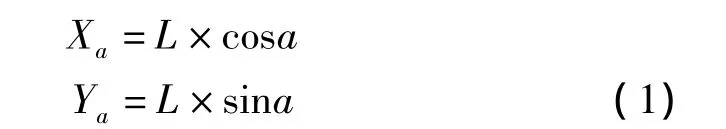
目标M的二维坐标为

其中

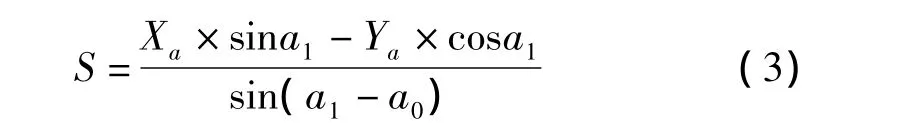
1.2 误差分析

测向交叉定位的基础是各观测站实现对目标辐射源的精确测向。受天线接收波束宽度的限制，传统雷达测向精度为2°～4°，所以当目标距离较远时，定位精度差［4］。如图2所示。

图2 测向精度对定位的影响

图2中a0、a1为O、A两观测站对目标M的无源探测方向，虚线为测向精度。当目标在四边形EFGH中任意一点分布时，都会被定位在M点。如果测角精度较大或目标较远，四边形EFGH范围较大，目标定位误差较大。

定位误差与参数Xa、Ya、a0、a1的测量误差 ΔXa、ΔYa、Δa0、Δa1有关。对式(2)求微分可得

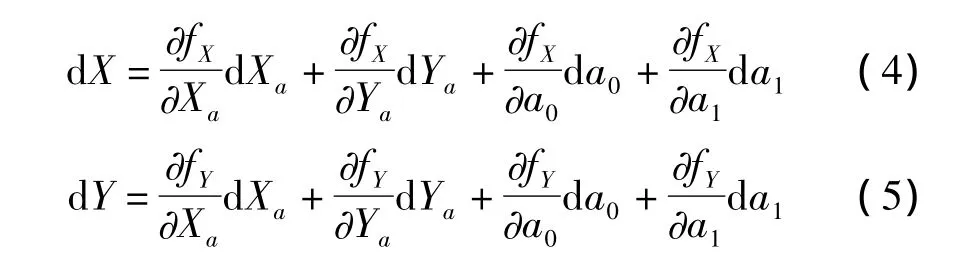
假设各项测量误差相互独立且服从零均值的高斯分布，即E［(Δx)］=E［(Δy)］=0。记E［(ΔXa)2］=E［(ΔYa)2］=σ2l，E［(Δa0)2］=E［(Δa1)2］=σ2a。当测量误差较小时，可以近似地用Δ代替式(4)、式(5)中的d，有

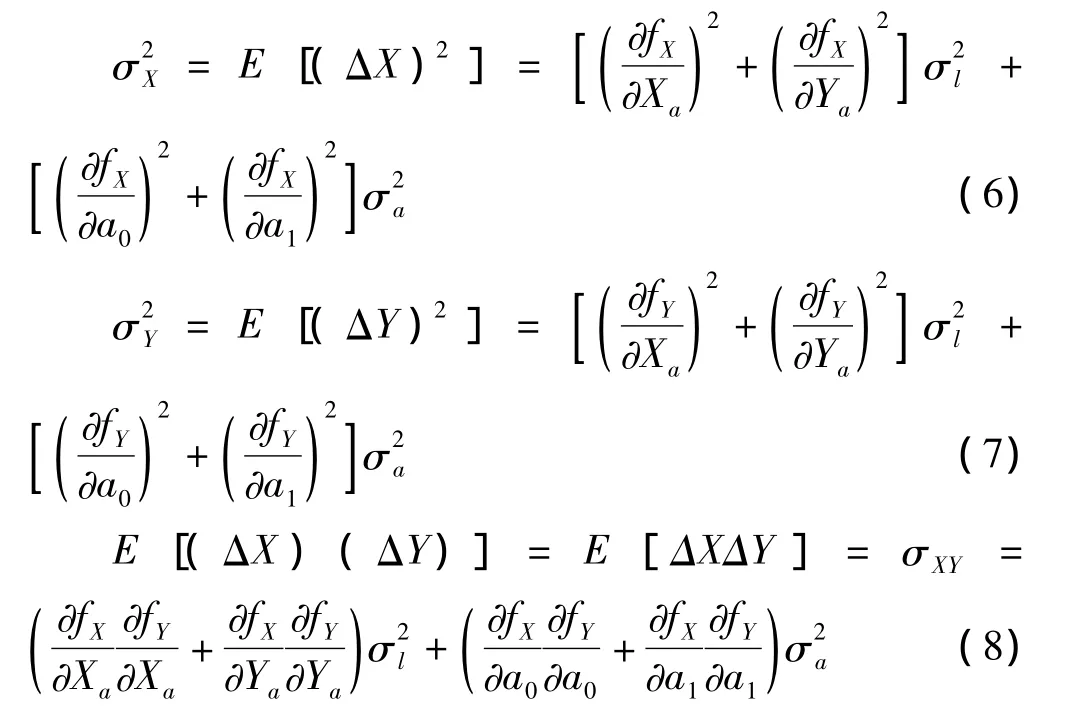
所以定位精度GDOP(Geometric Dilution of Precision)为

1.3 仿真GDOP曲线

图3～图6为各不同参数下测向精度几何分布图，对比得出各参数对测向精度的影响。图中X轴，Y轴坐标为目标位置坐标，图中曲线为测向精度的等高线，距中心线越远，精度越差，误差越大。测向精度对定位精度的影响，即σa单独作用时取(Xa，Ya)=(50 km，0 km)，σl=15 m 时有

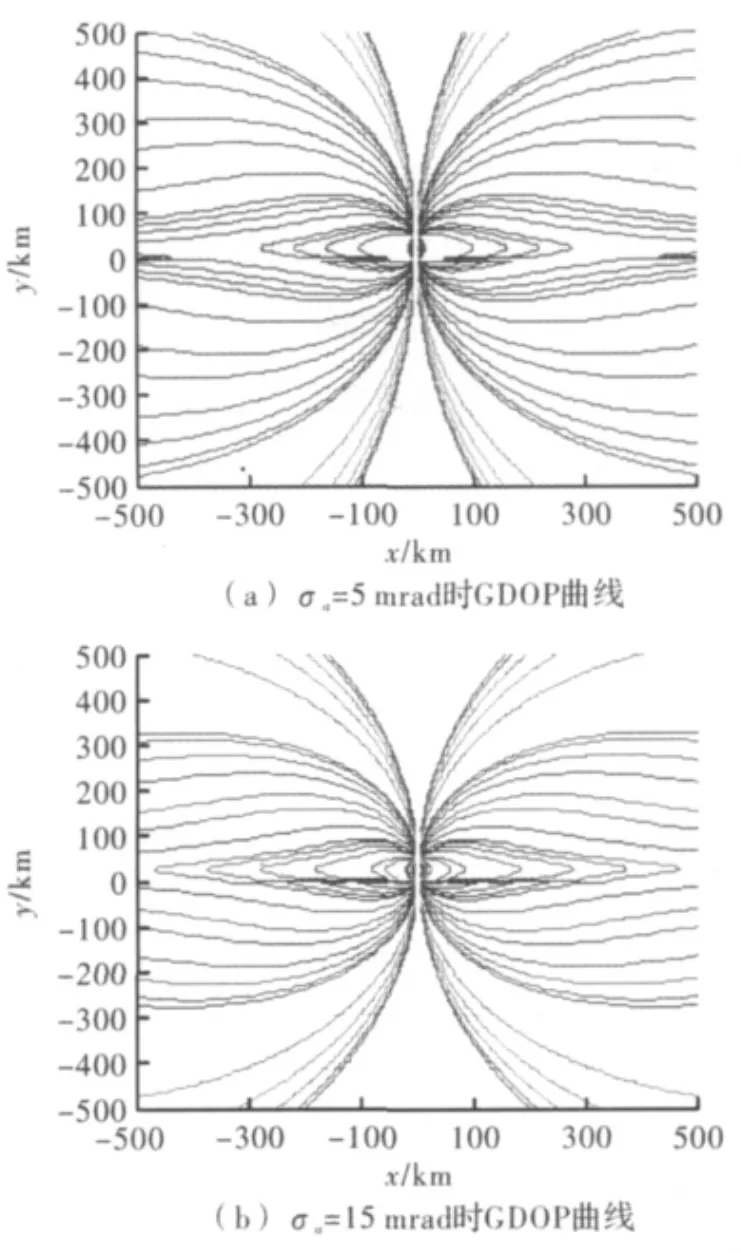
图3 不同σa时GDOP曲线

图3(a)中，GDOP曲线分布比较分散，等高线间距较大，说明随距离的增加误差增加较慢;而图3(b)中GDOP曲线分布比较紧凑，等高线间距较小，说明随距离的增加误差增加较快。两图中同一位置坐标下，图3(b)中误差大于图3(a)中的误差。由此可得测向精度越精准，定位误差越小。惯导位置精度对定位误差的影响取(Xa，Ya)=(50 m，0 m)，σa=5 rad 时，有

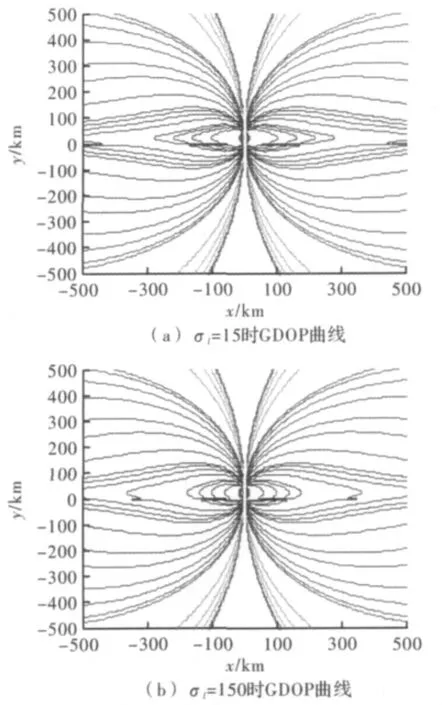
图4 不同σl时GDOP曲线

对比图4(a)和图4(b)，等高线疏密分布几乎相同，同一位置坐标的等高线基本一致，由此可知惯导位置精度对定位误差几乎没有影响。基线长度对定位误差的影响取σl=15 m，σa=5 mrad，有

图5 不同Xa时GDOP曲线

图5(a)中，GDOP曲线分布比较紧凑，等高线间距较小，说明随距离的增加误差增加较快;而图5(b)中GDOP曲线分布比较分散，等高线间距较大，说明随距离的增加误差增加较慢。两图中同一位置坐标下，图5(a)中误差要大于图5(b)中的误差，对比上两图可知，基线长度越大，定位误差越小。基站排放位置对定位误差的影响取σl=15 m，σa=5 mrad，L=50 km，有

对比图6(a)，图6(b)，图6(c)和图6(d)这4图，只是由于基站坐标的变化，等高线的中心和形状有所变化，而等高线疏密分布几乎相同，同一位置坐标的等高线基本一致，由以上4图可知，在基线长度一定的情况下，定位误差大小几乎不变，但具有方向性。

2 结束语

与有源定位相比，无源定位具有较突出的优点，是未来探测定位的发展方向。测向交叉定位接收机及信号处理相对比较简单，传统有源雷达的接收机及信号处理设备经改造可以完成无缘探测任务，便于对传统雷达进行组网。测向交叉定位采用窄波束搜索式测向，天线增益高，探测距离远。而且多站信号的相互匹配比其他无源定位方法容易实现。文中对侧向交叉定位精度进行研究，为现实交叉定位应用提供理论指导，使交叉定位在实现时能尽可能避免误差，精确定位。