开关磁阻电机的三维有限元分析

熊春宇 王艳芹 吴春梅 李欣欣

(大庆师范学院物理与电气信息工程学院，黑龙江 大庆 163712)

0 引言

目前，二维有限元分析在开关磁阻电机的磁场计算过程中得到了广泛应用。但受到理论知识不足的影响以及硬件条件的限制，很少有对开关磁阻电机整个场域进行三维有限元分析的研究。二维有限元分析在搭建模型时采用分步建模，这会存在一定的误差，不具有通用性。同时，由于模型简化带来的误差，对计算值也有较大的影响［1］。本文采用的三维建模方法正是基于整体建模的方法，利用三维有限元数值进行分析计算，可以准确描述开关磁阻电机的端部磁场效应，使磁场的计算更为精确。

1 三维有限元与二维有限元的比较

二维有限元分析对计算机硬件环境要求不高，计算速度较快。在对端部效应要求不严格的情况下，该方法也能基本满足有限元分析的要求;而且与解析法相比较，该方法所得到的结果也较为理想，在电磁场分析中也得到了一定的应用。二维有限元在研究时忽略了端部磁场效应，而当转子在极对槽的位置附近时端部磁场效应是比较严重的。由端部磁场效应引起的误差可能会达到33%左右，这种误差在一些要求较高的电磁计算中是不能被忽略的。采用二维计算时，只能计算绕组的平面有效部分，而无法计算端部特性和端部漏感，从而无从考虑端部效应对电感和转矩等电机参数的影响。解决以上这些问题的有效方法就是采用三维有限元数值计算［2］。

2 开关磁阻电机的三维电磁场分析

由于开关磁阻电机在不对齐位置下端部的磁场非常严重，要精确计算电机的磁链特性，就必须采用三维有限元分析法［3］。虽然三维有限元方法早在1980年就用于电机的磁场计算，但长期以来，广大研究人员仍采用二维有限元计算，然后再用修正系数补偿端部磁场的计算误差［4］。其根源在于三维有限元分析对计算机硬件环境要求很高，且三维电磁场分析有限元软件不易获得。

本文采用有限元分析软件ANSYS，完成开关磁阻电机的三维有限元分析。

2.1 三维有限元模型

本文对一台3 kW、四相(8/6极)开关磁阻样机进行三维有限元分析，电机结构尺寸如表1所示。

表1 样机结构尺寸Tab.1 Structure sizes of the prototype

根据样机的结构参数，建立的开关磁阻电机三维有限元模型如图1所示。

图1 三维有限元模型Fig.1 Three-dimensional finite element model

2.2 基本假设

考虑到三维有限元分析的基本原理及求解方式，再结合电机的实际结构，在进行三维有限元分析前，作如下基本假设［5］。

①单位长度的导线上，电流处处相等;

②电机定转子及转轴的材料磁化曲线是单值函数;

③不考虑电机轴，且认为电机外壳和电机轴不会产生漏磁;

④忽略轴承及轴承室的影响，整个电机轴具有相同的直径。

2.3 数学方程

在三维计算中，采用标量磁位φ对开关磁阻电机进行有限元分析。这里引入一个新的概念“跑道线圈”，它可以作为一个特殊的单元，区别于电机剖分单元。采用跑道线圈来表示电流源，对电机施加载荷［6］。这样做的好处是在有限元模型剖分时，不必考虑电流源的作用，而是把它当作剖分模型以外的部分。对于无源静态磁场，可以将麦克斯韦方程写成如下形式:

在电机定转子极部和轭部，磁场可用磁标量ψ表示为:

假设在铁磁材料与空气的交界处有A、B两点，在这两点处的磁标量可表示为:

所求得的整个场域上边值问题为:

式中:Ω1、Ω2分别为电机内外圆周表面。

采用三维有限元分析，在进行有限元剖分之前，需要确定剖分对象的形状函数。考虑到计算机硬件环境的限制以及剖分的效果，本文采用四面体单元进行分析求解［7］。四面体剖分单元如图2所示。

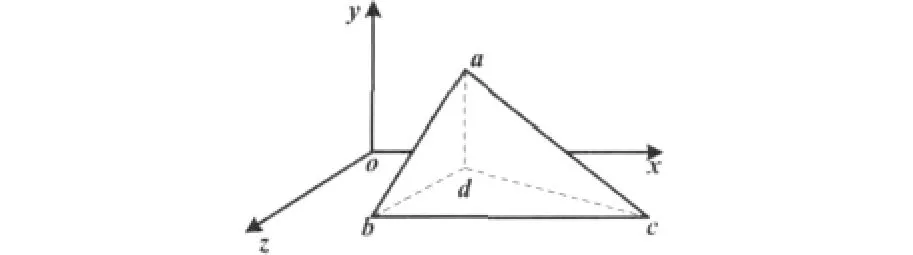
图2 四面体剖分单元Fig.2 Tetrahedralization split unit

四面体单元由四个三角形构成，单元的四个节点分别用a、b、c、d表示，并按照右手螺旋关系编号。四面体单元内任一位置的磁位ue为x、y、z的线性函数，可表示为:

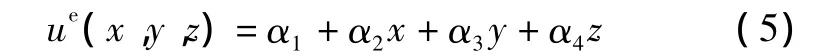
设节点 a、b、c、d 对应的坐标分别为(xa，ya，za)、(xb，yb，zb)、(xc，yc，zc)、(xd，yd，zd)，对应的磁位分别为，则有:

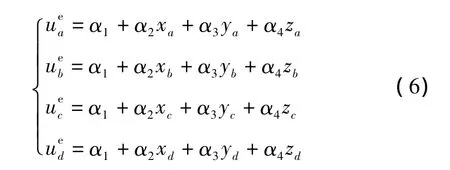
由式(6)可得 α1、α2、α3和 α4，并将结果代入式(5)，可得:

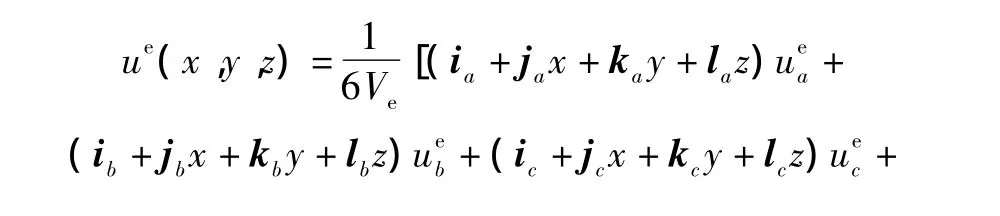
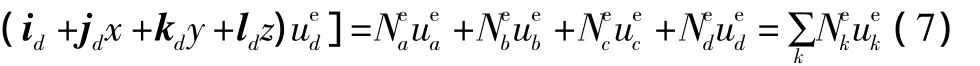
式中:k=a，b，c，d。

式中:x、y、z为单元e内P点的坐标;Vc为P点和面bcd所组成的子四面体的体积。

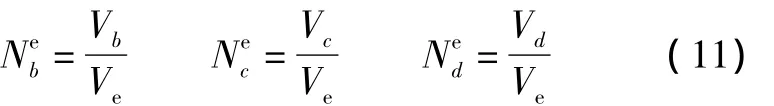
式中:Vb为P点和面acd所组成的子四面体的体积;Vc为P点和面bcd所组成的子四面体的体积;Vd为P点和面abc所形成的子四面体的体积。

3 三维有限元分析的前处理

三维有限元分析包括电机模型的建立、单元类型定义、模型赋材质和网格划分［8］。

在三维模型的建立过程中，需要考虑铁心的长度(取为0.18 m)。本文采用图形用户界面(graphical user interface，GUI)方式对电机整体建模。当电机位置角θ=30°时的三维模型如前文图1所示，经搭接后，将各实体之间的缝隙消除，实现真正意义上的相关联。

本文采用的三维剖分单元是SOLID98四面体单元，该四面体有10个节点。SOLID98单元不用设置实常数，模型中的材料区域包括空气、铁磁材料和绕组，其中，通电线圈采用ANSYS提供的跑道线圈。三维分析中定义的材料参数如下。

①空气区的相对磁导率为1.0;

②铁磁材料的B-H曲线根据厂家提供参数取近似单值函数;

③绕组部分统一分配，相对磁导率为1.0。

对电机赋完材质后的模型如图3所示。其中，图3(a)为最大电感位置即θ=30°时的模型，图3(b)为最小电感位置θ=0°时的模型。将赋完材质的所有实体用粘接(GLUE)命令融合到一起，使各实体边界融合，以满足第二类边界条件。

图3 三维赋材质模型Fig.3 Three-dimensional material model

由于三维网格划分对计算机硬件环境要求较高，在确保计算准确度的同时，减小工作量，采用适当的精确度剖分实体模型，所得三维网格剖分示意图如图4所示。

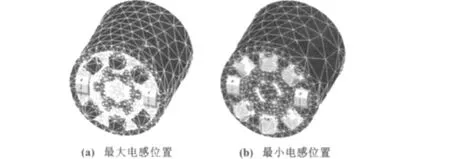
图4 三维网格剖分示意图Fig.4 Three-dimensional mesh split

从图4可以看出，在定转子极间气隙处，网格划分较密;而在其他部分，由于饱和现象不严重，剖分单元较大。跑道线圈是一个独立的基元，不进行网格划分。在剖分时可以忽略跑道线圈的存在，它对剖分结果无任何影响，只需在电流起作用的情况下考虑即可。

4 边界条件及载荷

三维有限元分析的求解区域是完整的电机模型。对整个立体圆周进行研究时，只考虑满足第一类边界条件，忽略第二类边界条件，计算可得在与磁力线垂直的磁标量位MAG=0。采用GUI或宏命令FMAGBC施加力的标志与二维分析的情况相同，它们均将转子定义为组件，并标志力和力矩。

在三维有限元分析过程中，引入了磁标势的概念。这时将电流源作为一个特殊的单元处理，它与电机的模型是两个独立的部分，定义电流源的单元属性为SOURCE36。这样做的好处是使电流源的作用不受电机模型的影响，易于建立电机模型，并便于施加载荷。跑道线圈的示例图如图5所示。

图5 跑道线圈Fig.5 Racetrack coil

“跑道线圈”考虑了电机定子绕组的端部效应，充分反映了电机绕组的实际结构。

5 三维有限元分析的求解

采用三维有限元方法分析静态磁场时，通常采用磁标势法［9］。磁标势法分为以下三种分析方法。

①简化标势法:该方法用于分析无铁区或无电流源的模型;

②差分标势法:该方法用于有铁区，但是铁区不为磁场形成闭合回路的模型;

③通用标势法:该方法用于含铁区，且铁区又为磁场提供闭合回路的场合。

经过考虑，本文采用通用标势法对电机磁场进行求解。选择静态磁场分析，采用通用标势法，设置收敛精度为 0.001，完成求解［10］。

6 后处理及结果分析

当电流为16 A时电机的磁感应强度分布如图6所示。

图6 磁感应强度分布Fig.6 Distribution of magnetic induction density

磁感应强度矢量分布如图7所示。磁感应强度的大小充分反映了开关磁阻电机内部电磁场的强弱分布。从图7可以看出，在通电线圈附近，磁场较强，其他处磁场较弱。

图7 磁感应强度矢量分布Fig.7 Distribution of magnetic induction vector

磁场强度分布如图8所示。

图8 磁场强度分布Fig.8 Distribution of magnetic field intensity

磁场强度矢量分布如图9所示。磁场强度的分布反映了电机磁场源的强弱。根据磁感应强度的分布规律也可以看出，磁通总是沿着磁阻最小的路径闭合。在磁路的方向上，极间漏磁通分布较乱，特别在最小电感位置，除定转子极的主磁通路径外，其他部分磁通较乱。同时可知，电机存在严重的局部饱和现象，最严重区域在定转子极附近，这也说明端部效应对结果会有很大的影响，体现了三维有限元分析的必要性。磁场强度最大值集中在定转子极间气隙。

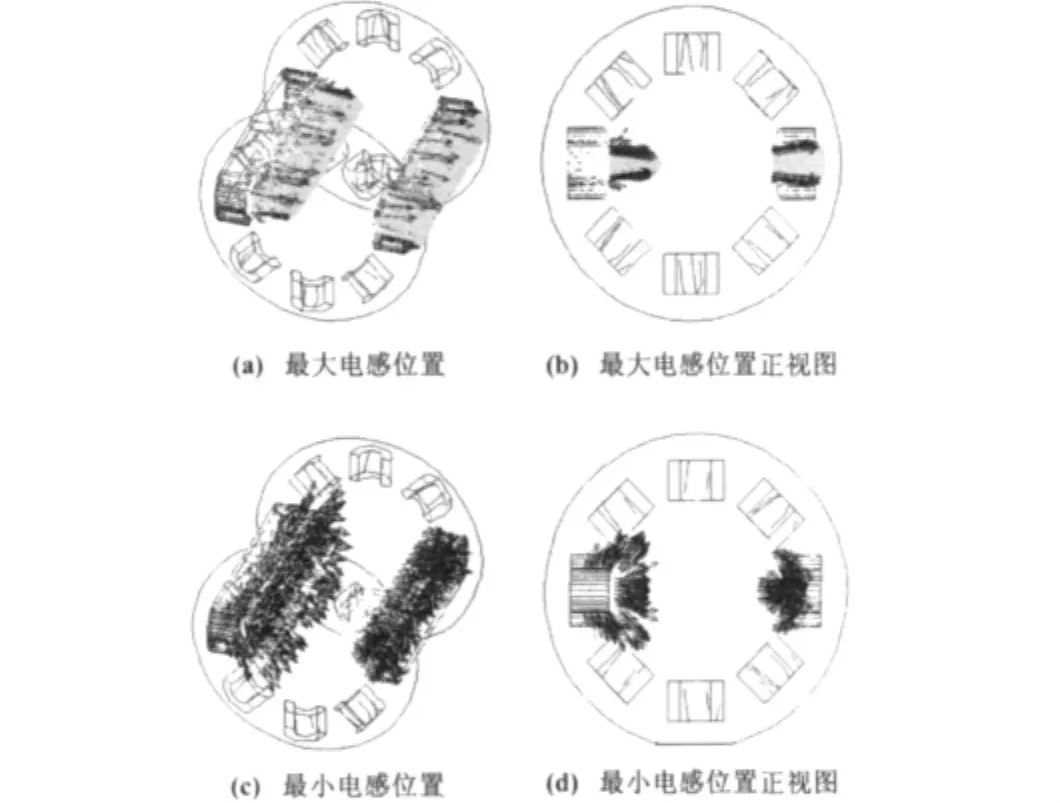
图9 磁场强度矢量分布Fig.9 Distribution of magnetic field intensity vector

7 结束语

本文对开关磁阻样机进行了三维有限元分析［11－14］，考虑了端部效应对磁场分布的影响，构建了三维分析下的数学模型。该模型的特别之处在于三维有限元分析加载电流时提出了“跑道线圈”这一概念，在考虑了端部效应的同时，也解决了立体模型施加载荷时出现的方向选择困难的问题。采用通用磁标势法对非线性方程组进行求解，得出了最大电感和最小电感位置处的磁感应强度和磁场强度分布。

［1］张成振.开关磁阻电动机磁场的二维有限元全场域计算与分析［J］.华南师范大学学报:自然科学版，1995(2):99－108.

［2］诸嘉慧.开关磁阻电动机电磁参数及静态特性的有限元分析［D］.哈尔滨:哈尔滨理工大学，2003.

［3］Bianchi N.Electrical machine analysis using finite elements［M］.Paris:Taylor Francis Group Press，2005:45 －70.

［4］Lee J Y，Lee B K，Sun T.Dynamic analysis of toroidal winding switched reluctance motor driven by 6-switch converter［J］.IEEE Transactions on Magnetics，2006，42(4):1275 －1278.

［5］Faiz J，Pakdelian S.Finite element analysis of a switched reluctance motor under static eccentricity fault［J］.IEEE Transactions on Magnetics，2006，42(8):2004 －2008.

［6］Ohdachi Y.Optimum design of switched reluctance motors using dynamic finite elementanalysis［J］.IEEE Transactionson Magnetics，1997，33(2):2033 －2036.

［7］Rahman K M，Fahimi B，Suresh G，et al.Advantages of switched reluctance motor applications to EV and HEV:design and control issues［C］//IEEE Transactions on Applications，2000:111 －121.

［8］陈燕，杨松，王振民.ANSYS软件在开关磁阻电机电磁分析中的应用［J］.煤炭科学技术，2001(4):20－22.

［9］李时伟.开关磁阻电动机参数分析及控制系统研究［D］.哈尔滨:哈尔滨工业大学，2007.

［10］贺小艳.开关磁阻电机磁场有限元分析及动态特性仿真［D］.太原:太原理工大学，2007.

［11］江缉光，刘秀成.电路原理［M］.2版.北京:清华大学出版社，2007.

［12］马春燕.微机原理与接口技术:基于32位机［M］.北京:电子工业出版社，2007.

［13］田金云，张广超，孟艳霞.基于单片机的LED汉字点阵显示系统设计［J］.工业控制计算机，2008，21(6):87 －88.

［14］吴国忠，许懿洋.步进电机驱动电源的设计及其可靠性分析［J］.中小型电机，2003，30(6):50－55.