全船结构静动态优化设计

周素素，夏利娟

近年来，优化技术广泛应用于结构设计中。船舶结构优化设计就是要寻求合理的结构形式和适当的构件尺寸，使船体结构在满足强度、刚度、稳定性和频率等要求下具有较好的力学性能、工艺性能、经济性能和使用性能。在船体结构优化设计中，相关静力学性能指标的约束能使船体结构的应力分布更趋均匀合理，实现船体结构的轻量化，相关动力学性能指标的约束可以有效避免船体结构与外界激励发生共振，解决日益突出的结构振动问题［1］。因此，能在满足结构规范要求的前提下，优化全船结构尺寸，以期获得消耗钢料最少且具有良好动力特性的船体结构，具有重要的工程实际应用价值。

目前，船体结构优化问题大多局限于中横剖面［2］、框架［3］、板架［4－6］、横舱壁［7－8］和舱段［9－10］等结构。由于船舶的工作环境非常复杂，除自身和设备的质量外，还要承受风、浪等多种载荷工况的组合作用，这对船舶结构的静、动力学性能设计提出了更高的要求。另外，全船结构优化拥有大量的设计变量和众多的约束条件，这也导致全船优化往往难以进行，所以针对全船的结构优化设计较少。

本文基于自适应模拟退火优化算法，以某自航绞吸挖泥船为研究对象，结合优化软件iSIGHT，建立了全船结构优化的数学模型，最终实现了全船结构静动态优化设计。

1 灵敏度分析

大型船舶具有众多的板材厚度和骨材规格，如果将所有板材厚度和骨材规格作为设计变量直接进行优化，其计算量和耗时量都是相当巨大的，优化效率会很低，致使优化问题往往难以进行。因此，灵敏度的计算与分析是全船结构优化设计中极为重要的一步。

计算目标函数、约束函数对设计变量求导的过程称为灵敏度分析，它反映了设计变量的改变对目标或约束函数的影响。DOE［11］是一种以概率论和数理统计为理论基础，经济地、科学地安排实验的一项技术。DOE技术的参数试验方法采用类似差分的思想，假设回归方程y=f(x1，…，xi)，通过计算设计变量xi水平上的微小摄动dxi对响应y的影响dy来求解各设计变量的灵敏度Sxi，然后采用归一化方法求解出各设计变量的归一化灵敏度。归一化结果消除了各响应在数值量级上的极大差异，更能有效地比较各响应灵敏度，其计算公式为:

式中:Nxi有正有负，为各设计变量灵敏度Sxi与灵敏度数值总和的比值，即各设计变量灵敏度所占的百分比，且 Σi|Nxi|=100。

因此，本文采用参数试验方法进行DOE分析，计算出全船结构设计变量对各响应的归一化灵敏度，并以此作为依据筛选出优化模型的设计变量。

2 优化模型

2.1 数学模型

一般问题的优化模型的数学表达式为:

求x={x1x2…xn}T

使 min f(x)

式中:xi为设计变量，n为设计变量总数，f(x)为目标函数，gk(x)为约束函数为设计变量xi的下限与上限，{x1x2… xn}T为设计变量组成的列向量。

2.2 目标函数

以全船结构质量最小化为优化目标。

2.3 设计变量

全船的设计变量分为两类，一类为板材设计变量，一类为骨材设计变量。板厚变量为整型，骨材变量通过在 MSC.Patran 中建立型材库作为离散集［12－13］，优化时骨材规格的变化从该离散集中取值，骨材的所有参数优化时进行统一的尺寸变化;两种变量均为离散型。

2.4 约束条件

约束主要有几何约束、应力约束、变形约束以及频率约束。

2.4.1 尺寸约束

2.4.2 应力约束

2.4.3 变形约束

式中:umax为全船最大变形值，［u］为许用变形值。

2.4.4 频率约束

式中:fi为第i阶垂向固有频率;fimin、fimax分别为频率禁区的下限和上限;ns为频率约束个数。

2.5 优化方法

本文优化针对大型船舶全船结构，优化问题包含的设计变量比较多，响应与变量之间的关系是高阶非线性的，设计空间非连续，这导致优化问题难以进行。

自适应模拟退火算法(Adaptive Simulated Annealing，ASA)是一种高效快速的全局优化算法，用以解决具有多峰和非光滑性的高难度非线性优化问题。ASA算法是基于Monte Carlo迭代策略的一种随机寻优算法，其出发点基于物理退火过程与组合优化之间的相似性，由较高初温开始，利用具有概率突跳特性的Metropolis抽样策略在解空间进行搜索，伴随温度的不断下降重复抽样过程，最终得到问题的全局最优解。ASA算法具有对变量性质无要求、对初始条件的要求低，不依赖初始解、肯定收敛且收敛速度快的优点，非常适合于求解离散设计变量问题。因此，本文优化设计采用自适应模拟退火算法。

2.6 优化流程

根据船体结构设计优化特点，基于自适应模拟退火算法的全船结构优化设计流程见图1。

图1 全船结构优化设计流程Fig.1 Optimum design flow of whole-ship structure

3 工程实例

以某自航绞吸挖泥船全船结构为研究对象建立模型，进行优化分析。

3.1 全船有限元模型

全船结构有限元模型采用板壳单元和梁单元组合模型。船上舾装设备的模拟是通过在质心位置建立质量点，用MPC将质量点与船体相应接触部分进行刚性连接［14］;各舱室内液体压力是通过在相应舱室内建立质量点来模拟。

3.2 附连水质量

估算船体振动模态时必须考虑附连水质量效应。本文采用刘易斯图谱法计算附连水质量，通过将船体沿船长方向分为不等间距小段，根据刘易斯经验公式以质量点的形式作用到船壳水线以下的单元节点上。根据上述内容计算附连水质量，加载附连水质量后的全船结构有限元模型见图2。

图2 全船有限元模型Fig.2 FE model of whole-ship

3.3 频率禁区

引起船体振动的主要激励源是主机和螺旋桨。本文考虑船体垂向振动一阶和二阶固有频率，使其与螺旋桨转速保持一定差距，建立两个频率禁区。根据设计者要求设定频率禁区约束条件为:

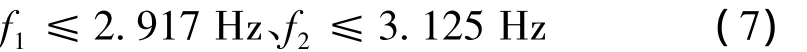
式中:f1为第一阶垂向固有频率;f2为第二阶垂向固有频率。

3.4 全船结构模态分析

采用Lanczos方法提取全船结构前两阶垂向振动固有频率，固有频率计算结果见图3和图4，并将固有频率数值结果汇总于表1。

表1 全船垂向振动固有频率Tab.1 Vertical vibration natural frequencies of whole-ship

从表1可以看出，船体结构第二阶垂向振动固有频率不满足式(7)频率禁区约束条件的要求，容易发生共振现象，因此有必要对全船结构进行优化。

图3 第一阶垂向固有振型Fig.3 The first-order vertical natural vibration modes

图4 第二阶垂向固有振型Fig.4 The second-order vertical natural vibration modes

3.5 灵敏度分析结果

采用参数试验方法对自航绞吸挖泥船全船结构进行各设计响应的灵敏度计算。全船的设计变量共有111个，设计变量庞大，在本文的动力特性优化设计中，主要考察全船结构的第二阶垂向固有频率和质量，采用灵敏度比值的方法来筛选设计变量。根据参数试验方法得到的第二阶垂向固有频率灵敏度和质量灵敏度的计算结果，计算二者之间的比值关系，结果见图5。根据计算结果剔除灵敏度比值比较小的设计变量，最终选取了80个设计变量。

图5 第二阶频率灵敏度与质量灵敏度比值Fig.5 Ratio of second-order frequency sensitivity and mass sensitivity

3.6 优化设计

优化模型的数学表达式为:

式中:目标函数为全船结构质量W最小化;σVonmises为Von-mises应力，τ为剪应力，σ梁为梁单元的合成应力，umax为最大变形;f1、f2分别为第一阶和第二阶垂向振动固有频率;xi为设计变量，上标l和u为设计变量的下限和上限。

3.7 优化结果与分析

采用自适应模拟退火算法对上述优化模型进行分析，优化仿真系统经过148 h 48 min达到收敛。目标函数W的迭代历史见图6;设计变量的初始值与最优解对比结果见表2;优化前、后的优化目标全船结构质量W，结构的第一阶、第二阶垂向固有频率以及强度计算的对比结果汇总于表3。

图6 目标函数的迭代历史(单位:t)Fig.6 Iteration history of objective function

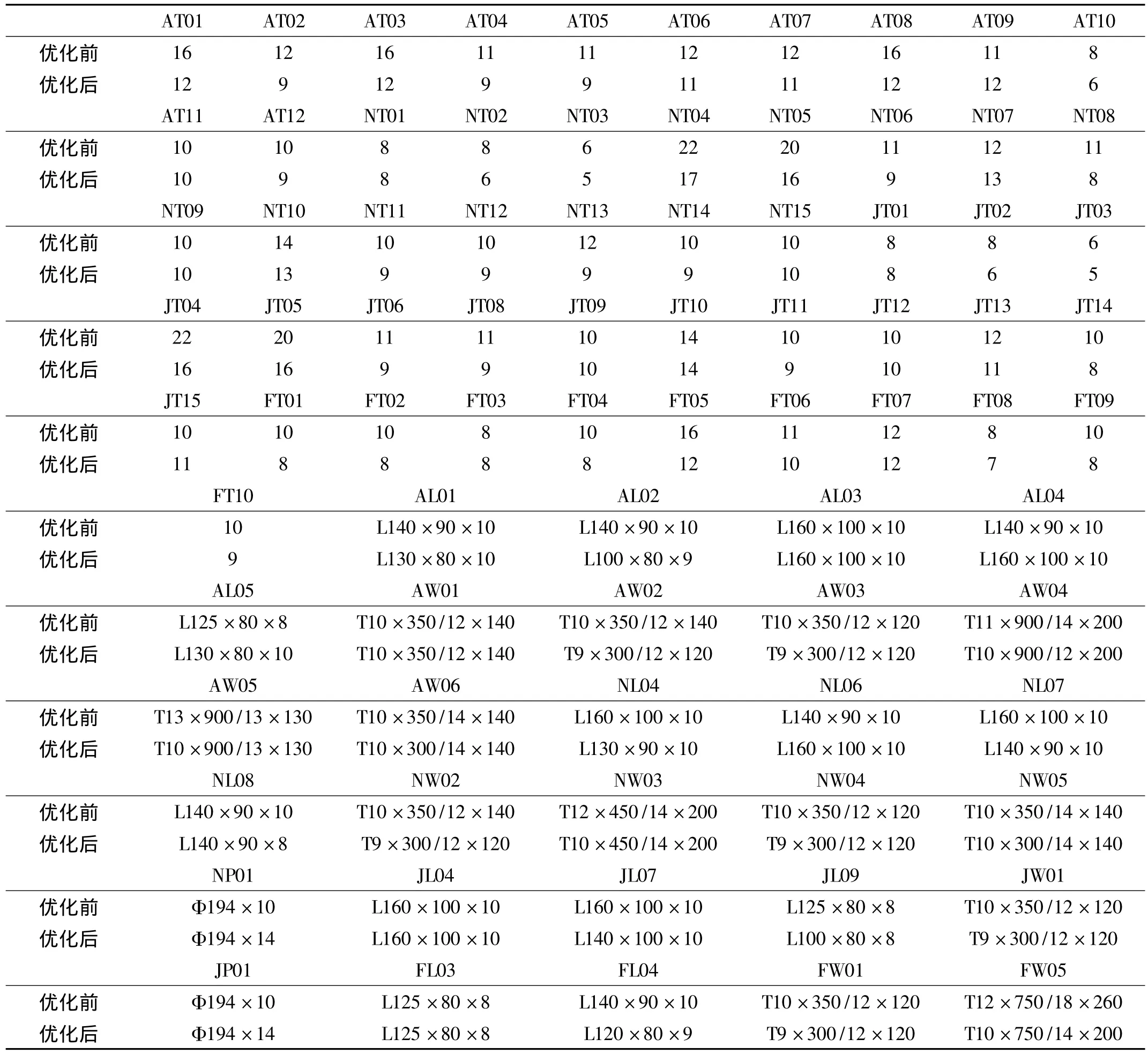
表2 设计变量初始值和最优解对比(单位:mm)Tab.2 Comparison of initial value and optimum value of design variables

表3 各参数优化前后对比Tab.3 Comparison of initial value and optimum value of each parameter

从上述结果可以看出:

(1)优化后的结果在可行域内，属于有效解集，即满足所有应力、变形以及频率约束。

(2)除了少数设计变量如尾封板板厚(AT09)，尾封板扶强材规格(AL04)，泥泵舱平板龙骨板厚(NT07)等之外，大部分设计变量的尺寸规格均有所减小，且板材厚度减小幅度比较大，这说明板材厚度对固有频率及结构质量的影响比骨材规格大，这与本文对各个变量进行的灵敏度分析结果是一致的。

(3)优化后全船结构总质量为3 279.951 t，与初始的3 403.407 t相比减轻 123.456 t，即减轻 3.627%。这说明，本文优化能达到减轻船体结构钢料，降低工程造价的效果。

(4)优化后第一阶和第二阶垂向固有频率均有所降低。第一阶频率降低0.107 3 Hz，即降低5.579%;第二阶频率降低0.219 0 Hz，即降低6.570%，增加了结构的频率储备，降低了发生共振的概率。尤其第二阶垂向固有频率值优化后小于3.125 Hz，达到了优化的初始目标。

3.8 优化方案比较

上述优化分析模型是在满足频率约束条件下，达到全船结构质量极小化的优化目标。另外，本文还建立了在质量约束条件下，达到船舶结构固有频率极小化的优化模型，即通过优化板材厚度和骨材型号等离散变量，使结构在满足相应的质量、强度、变形约束和几何限制等条件下，以全船结构固有频率极小化为优化目标。

采用自适应模拟退火算法对第二种优化模型进行求解分析，直至目标函数全船结构第二阶垂向振动固有频率f2达到收敛。两种优化方案下最优结构的全船结构质量和第一阶、第二阶垂向振动固有频率的对比结果汇总于表4。

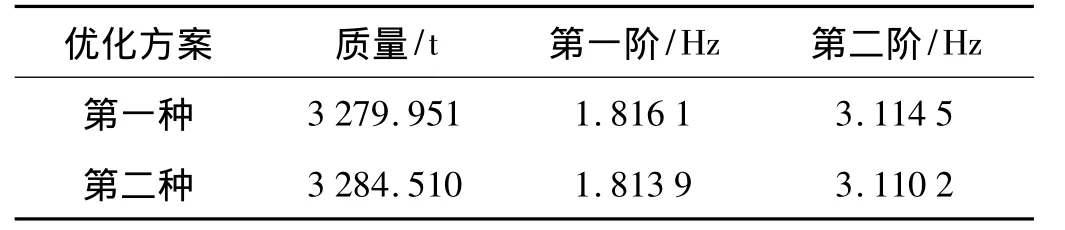
表4 两种方案优化结果对比Tab.4 Comparison of two optimization programs’optimum result

从优化对比结果可以看出，第二种优化模型以固有频率为优化目标，因此获得的最优解减重效果略差于第一种优化方案，但减振效果较好。事实上，两种优化方案的最优解比较接近，优化效果相当。这说明，对于优化问题，优化目标和约束函数均能起到很好的限制作用，合理地安排优化目标及约束条件的上下限，有益于获得一个各项性能均良好的船体结构。

4 结论

本文以某绞吸挖泥船为研究对象，采用DOE技术的参数试验方法对全船几何特性参数进行灵敏度分析，找出了对设计目标影响比较显著的几何特性参数作为有效的设计变量。分别以全船结构重量最小化和第二阶垂向振动固有频率为优化目标建立了船体结构的静动态优化模型，并进行优化求解分析。优化后的结构在满足强度和刚度的条件下，不仅减重效果更是显著，且达到了频率禁区的要求，降低了发生共振的概率，具有重要的工程使用价值。

［1］黄海燕，林志祥，王德禹.船艉结构静动态多目标优化设计［J］.船舶力学，2011，15(11):1270－1277.HUANG Hai-yan，LIN Zhi-xiang，WANG De-yu. Multiobjective optimization of ship stern under static and seismic loading［J］.Journal of Ship Mechanics，2011，15(11):1270－1277.

［2］许华文，肖 熙.基于模拟退火算法的舰船中剖面优化设计［J］.上海交通大学学报，2000，34(1):95－98.XU Hua-wen，XIAO Xi.Optimum design of midship section based on simulated annealing algorithm［J］.Journal of Shanghai Jiaotong University，2000，34(1):95－98.

［3］刘土光，谭林森，曾广武.受局部强度约束的船舶框架和板架结构的优化设计［J］.武汉造船，1984(5):1－12.LIU Tu-guang，TAN Lin-sen，ZENG Guang-wu.Optimum design for frame and grillage structure with constraints of local intensity［J］.Wuhan Shipbuilding，1984(5):1 －12.

［4］林 哲，赵德有.船体板架动力优化设计［J］.船舶工程，1998(6):9－11.LIN Zhe，ZHAO De-you. Optimum dynamic design for grillage structure［J］.Ship Engineering，1998(6):9 －11.

［5］强兆新.船体板梁组合结构频率禁区动力优化研究［D］.大连:大连理工大学，2005.

［6］何 勇，夏利娟.一种基于MATLAB和Nastran的船体结构优化程序研究［J］.船舶工程，2011(2):132－134.HE Yong， XIA Li-juan. A study on a ship structural optimization program based on MATLAB and Nastran［J］.Ship Engineering，2011(2):132－134.

［7］ARAI MAKOTO，SHIMIZU TAITO，SUZUKI TATSUHIRO.Optimization of transverse bulkhead design by response surface methodology［J］.Journal of the Kansai Society of Naval Architects，2000，234:237 －243.

［8］黄衍顺，陈 斌，涂跃红.双壳散货船结构重量优化设计［J］.机电设备，2007(1):3－6.HUANG Yan-shun，CHEN Bin，TU Yue-hong.Optimization of structure and hull weight of double hull bulk carriers［J］.Mechanical and Electrical Equipment，2007(1):3 －6.

［9］ Kitamura M，Nobukawa H，Yang F X.Application of a genetic algorithm to the optimal structural design of a ship＇s engine room taking dynamic constraints into consideration［J］.Journal of Marine Science and Technology，2000，5(3):131－146.

［10］艾海峰，陈志坚，陈炜然，等.超小水线面船主机舱段结构优化设计［J］.船海工程，2007，36(2):25－27.AI Hai-feng， CHEN Zhi-jian， CHEN Wei-ran， et al.Structural optimal design of the main frame of microminiature waterplane area yacht［J］.Ship ＆ Ocean Engineering，2007，36(2):25－27.

［11］ Engineious.iSIGHT User’s Guide(v9.0)［M］.2004.

［12］王从晶，夏利娟.全船结构动力特性的优化设计研究［D］.上海:上海交通大学，2011

［13］何 勇，夏利娟.考虑动态响应特性的全船结构多目标优化研究［D］.上海:上海交通大学，2012.

［14］王从晶，夏利娟.全船有限元结构分析的若干关键技术［J］.上海交通大学学报，2010，44(6):768－773.WANG Cong-jing，XIA Li-juan.Several critical technologies of the whole-ship structural analysis through FEM［J］.Journal of Shanghai Jiaotong University，2010，44(6):768－773.