基于CPWP混合原子分解的滚动轴承故障诊断方法研究

姜锐红，刘树林，刘颖慧，唐友福，2

滚动轴承是应用极其广泛的零部件，它的失效是导致设备故障的最主要原因之一，因此，对滚动轴承进行状态监测与故障诊断，尤其是早期诊断，显得尤为重要。滚动轴承最常见的初期缺陷形式是表面点蚀，缺陷的存在会引起周期性冲击振动，它的频率(故障特征频率)取决于故障部位、转速和轴承参数［1］，通过故障频率的提取可判断失效的位置。

轴承发生故障时产生的周期冲击信号调制于机械系统的某一固有频率，经典的滚动轴承故障诊断方法是找到该调制信号的载波频率，再做窄带包络解调，但由于实际系统的复杂性，往往不可能准确找到系统固有载波频率，因此，经典的窄带解调方法有时不能很好地满足滚动轴承故障诊断的需要［2］。此外，时频分析信号处理方法如短时傅里叶变换、Wigner-Ville分布以及小波分析、经验模式分解(EMD)、循环平稳分析等现代信号处理方法在滚动轴承故障诊断中也得到广泛应用，然而，这些方法对信号的分解是唯一的，不具备自适应性，而使用特定过冗余字典将信号进行优化稀疏分解的原子分解是一种具有自适应性和灵活性的方法［3］。在故障诊断领域中，傅里叶原子库、小波原子库、脉冲原子库以及线性调频原子库的应用，学者们已做了一些研究［4－8］，本文根据余弦包对信号的能量集中性适合提取信号主要能量频率成份的优势，结合小波包对冲击信号的敏感性，利用CP及WP的快速算法，设计了CPWP混合原子库的匹配追踪快速算法，并将其应用于滚动轴承故障仿真与实测信号的分析，结果表明CPWP混合原子分解可得到信号更多有用信息，便于提取冲击调制信号特征。

1 混合原子分解

1.1 原子分解

参数化字典是过完备的，即字典中一些原子可由其它一些原子的线性组合表示，这使得信号可以在众多表示中选择最合适的分解形式，也即信号表示的自适应性。

1.2 小波包原子库

小波函数具有很强的瞬态和时域局部特性，是分析处理非平稳瞬时信号的有效工具。小波包分解是在小波分解的基础上对高频部分做进一步分解，可以在时间与频率分辨率之间得到好的折中，同时可为信号的分析提供更加冗余的原子波形，增强自适应选择的灵活性。

本文用到的正交小波包字典由子空间的正交归一基依尺度参数j、平移参数k以及子空间参数p的变化构成:

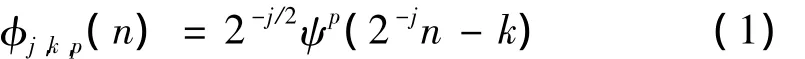
式(1)中 j为 2的整数次幂，k取整数，p=0，1，…，2j－1－1。

对于给定的尺度j，小波包共有2j个子空间，记为为每一次分解的低频部分，中的正交归一基为(n)。给定中的尺度函数及相应的滤波器系数，即可递推得到小波包各子空间的基函数:

其中:h0(k)为低通滤波器系数，h1(k)为高通滤波器系数，二者构成共轭正交镜像滤波器组。p=0时，基函数ψp(2－jn－k)=ψ0(n－k)即是中的尺度函数。

1.3 余弦包原子库

余弦变换是正弦变换家族中的一种变化，与傅里叶变换有着密切的联系，可应用快速傅里叶变换算法取实部得到。

Ahmed与Rao于1974年首先给出了离散余弦变换(DCT)的定义，后演变出八种DCT类型，本文采用DCT －IV 形式，给定序列 x(n)，n=0，1，…，N －1，其离散余弦变换定义为:

其中:k=0，1，…N－1，为 N点 DCT的频率采样点，可视为频率变化参数。

根据式(3)的变换形式，其核函数即为依频率变化的余弦变换原子:

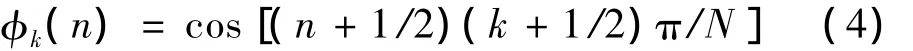
在余弦包中，给定分析信号长度及分解层数，可根据式(4)推导出各层原子的统一表达形式。与小波包分解不同的是离散余弦包变换的每一层不是将上一层的频率二进分割，而是对信号在时间域内二进分割。每一层将信号对应的时间段进行离散余弦变换。离散余弦变换具有很强的能量集中特性，在信号处理中得到了广泛的应用。对于分解层数d，余弦包将信号分为2d段，每段由快速傅里叶变换求得该段信号的DCT，每层分解相当于信号的加窗DCT。因此，余弦包字典波形可由式(5)统一表达:

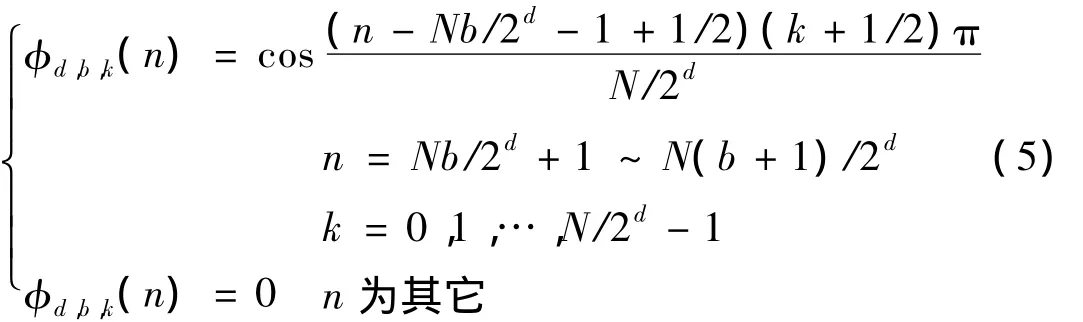
其中:n=0，1，…，N－1为原子中时间采样点，d为余弦包分层标号，b为各层分段标号，k为N/2d长度DCT变换的频域采样点。

1.4 CPWP匹配追踪算法

小波包字典包括小波函数在频率与时间范围扩展及平移的震荡波形集，余弦包字典由宽度与位置变换的窗函数截取的归一化变频余弦曲线集组成，CPWP混合原子库包含广泛的不同时频现象元素，对变时频结构的信号表达能力更强。将小波包与余弦包的快速算法应用于混合原子分解中，结合匹配追踪算法，设计得到CPWP混合原子分解的快速算法流程如图1所示。每次选择的混合分解最大系数，可根据其所在分解层及层内位置快速得到与该系数对应的原子波形，所以上述CPWP混合原子分解算法不需要事先构造原子库。

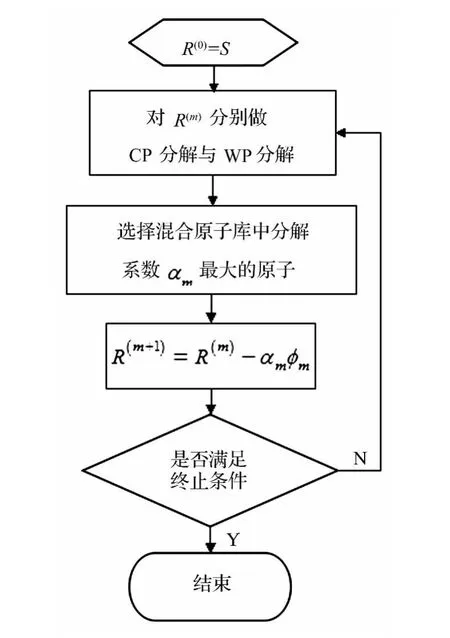
图1 混合原子分解流程Fig.1 Merged atomic decomposition flow chat

2 滚动轴承故障信号分析

2.1 滚动轴承故障仿真信号分析

滚动轴承元件发生单点局部损伤时，传感器拾取到的振动信号的数学模型可用式(6)表达［9－10］:

其中:A(kT)为kT时刻的冲击幅值，A(t)为幅值调制函数，T为故障特征周期，f0为轴承座－传感器系统的某一固有频率，α为对应的系统阻尼比，U(t)为单位阶跃函数。取A(t)为常数值1模拟滚动轴承外圈单点故障，T 取1/124 s，f0取4 000 Hz，α 取 500，采样频率 fs取25 000 Hz，仿真信号的时域波形如图2所示。

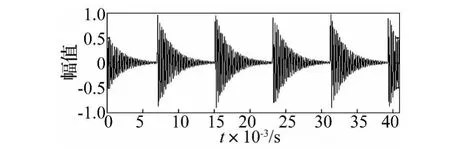
图2 滚动轴承外圈故障仿真信号时域波形Fig.2 Time waveform of outer race fault signal

对该仿真信号进行4层Cioflet3小波包原子分解，其分解的时频分布如图3所示，各个冲击特征在时域中基本清晰可辨，但载波频率模糊不可辨。图中横坐标为归一化时间坐标，最大值1表示所分析信号的最大采样时刻;纵坐标为归一化频率值，最大值表示1/2采样频率值(以下所有时频图的坐标意义均与该图相同)。该信号的4层余弦包原子分解时频分布如图4所示，冲击信号时域分辨率模糊不清，载波成份在频域内可清晰分辨。以上分析表明，Cioflet3小波包原子分解对冲击调幅信号的冲击信息在时域内分辨率较高，而余弦包分解对载波信息的频域分辨率较高。

将Cioflet3小波包与余弦包混合，应用1.4节设计的CPWP混合原子分解算法，对以上仿真信号做匹配追踪分解，如图5所示的时域分布图，得到较CP、WP原子分解更稀疏的表示，能准确反映冲击信号的时域位置，载波信号在频域的位置也很清晰。

2.2 滚动轴承实测故障信号分析

以Case Western Reserve University轴承数据中心的外圈故障试验数据［11］为例进行分析，试验轴承为6205－2RSJEM SKF深沟球轴承，采样频率fs=12 000 Hz，转速为1 748 r/min，计算得外圈故障特征频率为fout=104.4 Hz。取2 048个采样数据进行分析，信号的时域波形如图6所示。

图7为信号的Coiflet3小波包四层原子分解所得时频图，信号冲击时刻在时域中清晰可辨，但载波频率分辨率极低。图8为信号的4层余弦包分解，频域中能量集中的几个带较为明显，但时域内的冲击成份不能清晰显现。图9是应用四层CP与四层Coiflet3小波包的混合原子分解，经匹配追踪得到的时频表示，不仅频域内信号能量较集中的几个带较前两种方法清晰，时域内信号的冲击成份也很明显。

图3 外圈故障仿真信号小波包原子分解时频图Fig.3 Time-frequency plot of CP atomic decomposition

图4 外圈故障仿真信号余弦包原子分解时频图Fig.4 Time-frequency plot of CPatomic decomposition

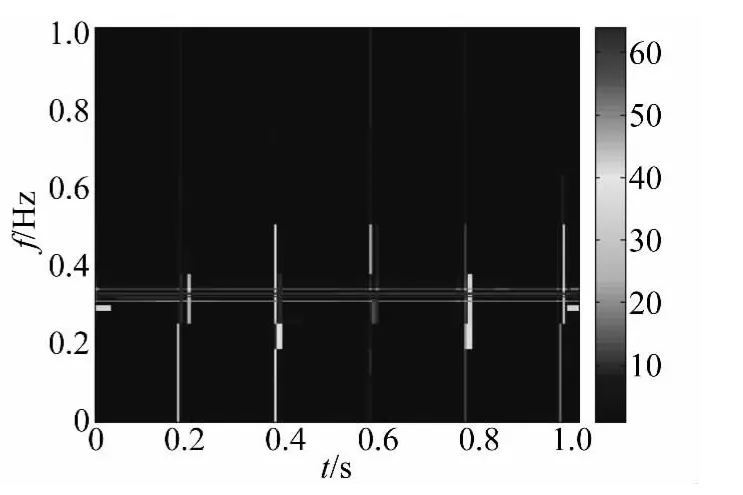
图5 外圈故障仿真信号CPWP原子分解时频图Fig.5 Time-frequency plot of CPWPatomic decomposition

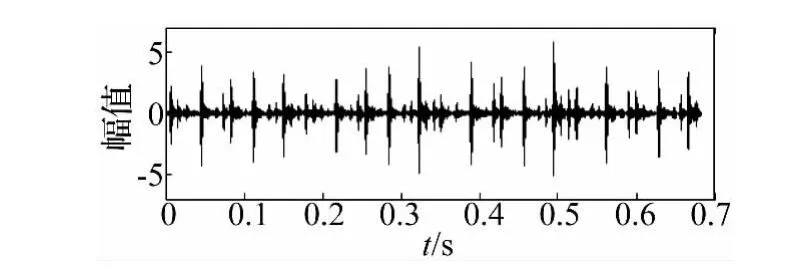
图6 滚动轴承外圈故障仿真信号时域波形Fig.6 Time waveform of outer race fault signal

在图9中，由Δt=(x1－x2)×(N－1)/fs可计算出任意两次冲击发生的时间间隔，其中x1、x2为两次冲击的横坐标，fs为信号采样频率，N为信号采样点数。计算得A、E之间时间间隔为0.144 s，相近于外圈故障理论冲击时间间隔(1/fout=0.009 6 s)的 15倍，由1/(ΔtAE/15)得到冲击频率为104.1 Hz，与轴承的理论外圈故障频率104.4接近。计算得AB、BC、CD、DE的时间间隔为 0.038 s、0.038 s、0.029 s、0.039 s，分别接近于4倍或3倍外圈故障理论冲击时间间隔。FC、GH、HE时间间隔均为0.009 7 s，与理论外圈故障冲击时间间隔接近。任意选择以上冲击时间间隔可计算得到接近于理论外圈故障频率的特征频率。

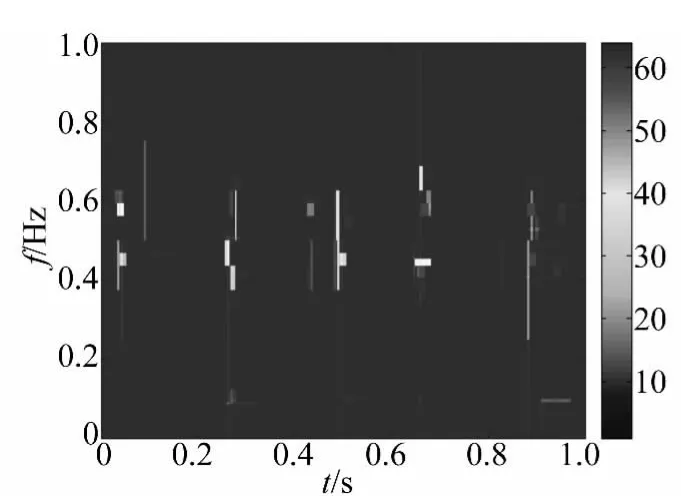
图7 外圈故障仿真信号小波包原子分解时频图Fig.7 Time-frequency plot of WP atomic decomposition

图8 外圈故障仿真信号余弦包原子分解时频图Fig.8 Time-frequency plot of CP atomic decomposition

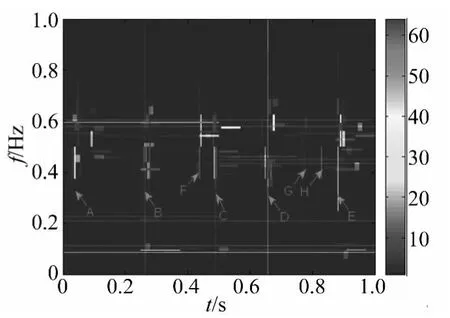
图9 外圈故障仿真信号CPWP原子分解时频图Fig.9 Time-frequency plot of CPWP atomic decomposition

判定滚动轴承故障必须是冲击与调制信息同时存在，冲击信息调制于轴承部件的固有频率，这个固有频率很难由测量或计算得到，因此确定解调中心频率及频带一直是滚动轴承故障诊断的一个难点。图9中，虽然整个频域范围内均可见有冲击信息，但在0.4～0.6(2 400～3 600 Hz)范围内，冲击成份比较集中，并且此处的整个时域范围有明显的固定频率，与仿真信号的分析结果对比，可判断冲击信号的载波频率落在此段频率范围内。相对于图7与图8，可见混合原子库分解提高了信号的分辨率，增加了信号分析的有用信息。

3 结论

信号在过完备字典库中的不唯一性表示，使得在众多表达中选择最适合信号分析目标的表示成为可能，不同字典的波形集与信号的匹配可从不同侧面反应信号特征，将不同字典波形集混合参与信号的匹配，可提供更加灵活的自适应能力，得到信号的更多有用信息。

通过对仿真信号及实测滚动轴承故障信号的分析表明，CPWP混合原子分解保持了CP、WP原子分解的稀疏性与高分辨率优势，并且将二者优势互补，能在时频域内提供更多冲击调制信号的有用信息，便于提取冲击信号及载波频率范围，适用于滚动轴承的故障诊断。

虽然混合原子分解可以提取滚动轴承故障特征，但从文中对实测信号的分析来看仍然存在特征信息不够突出，直观性不强，分析难度较大的问题，这将是下一步需要研究改进的内容。

［1］Nikolaou N G，Antoniadis I A.Rolling element bearing fault diagnosis using wavelet packets［J］.NDT ＆ E International，2002，35(3):197－205.

［2］Barszcz T，Jablonski A.A novel method for the optimal band selection for vibration signal demodulation and comparison with the Kurtogram ［J］.Mechanical Systems and Signal Processing，2011，25(1):431 451.

［3］Mallat S，Zhang Z.Matching pursuits with time－frequency dictionaries ［J］. IEEE Trans Signal Process， 1993，41(12):3 397－415.

［4］Feng Z P，Chu F L.Application of atomic decomposition to gear damage detection［J］.Journal of Sound and Vibration，2007，302(1－2):138－151.

［5］ Peng F Q，Yu D J，Luo J S.Sparse signal decomposition method based on multi－scale chirplet and its application to the fault diagnosis of gearboxes［J］.Mechanical Systems and Signal Processing，2011，25(2):549－557.

［6］唐海峰，陈 进，董广明.基于匹配追踪的复杂度分析方法在轴承故障诊断中的应用研究［J］.振动工程学报，2010，23(5):541－545.TANG Hai-feng，CHEN Jin，DONG Guang-ming.Research on application of matching pursuit based on complexity analysis method for fault diagnosis of rolling element bearings［J］.Journal of Vibration Engineering，2010，23(5):541－545.

［7］彭富强，于德介，罗洁思，等.基于多尺度线调频基稀疏信号分解的轴承故障诊断［J］.机械工程学报，2010，46(7):88－95.PENG Fu-qiang，YU De-jie，LUO Jie-si，et al.Sparse signal decomposition method based on multi-scale chirplet and its application to bearing fault diagnosis［J］. Journal of Mechanical Engineering，2010，46(7):88－95.

［8］冯志鹏，朱萍玉，刘 立，等.基追踪在齿轮损伤识别中的应用［J］.北京科技大学学报，2008，30(1):84 －89.FENG Zhi-peng，ZHU Ping-yu，LIU Li，et al.Application of basis pursuit to gear damage detection［J］.Journal of University of Science and Technology Beijing，2008，30(1):84－89.

［9］胡晓依，何庆复，王华胜，等.基于STFT的振动信号解调方法及其在轴承故障检测中的应用［J］.振动与冲击，2008，27(2):82 －86.HU Xiao-yi， HE Qing-fu， WANG Hua-sheng， et al.Vibration signal demodulation method based on STFT and its application in rolling bearing fault detections［J］.Journal of Vibration and Shock，2008，27(2):82－86.

［10］McFadden PD，Smith JD.Model for the vibration produced by a single point defect in a rolling element bearing bearing［J］.Journal of Sound and Vibration，1984，96(1):69 －82.