船舶线束寄生参数和串扰动态变化估计

王瑞宝，周诚祥

(92571部队，海南 三亚 572021)

0 前言

船舶上线缆、线束众多，线缆、线束内部导线通过耦合产生串扰，串扰能增长系统噪声，破坏数据，增强传导发射和辐射发射［1］，使得整个船舶电磁兼容性能 (electromagnetic compatibility，EMC)强烈下降。

寄生参数和串扰与导线对地高度和相互间距离有关。船舶航行时的加速、减速、震动以及由风、浪、涌造成的横摇和纵摇都会使线缆、线束内部导线的对地高度和相互间距离发生变化，寄生参数和串扰随之改变。对于寄生参数和串扰的动态变化预测，国内尚未开展，国外一些学者使用摄动理论［2］、神经网络［3－4］、分形理论等方法计算出寄生参数后，使用SPICE求得串扰。这些方法虽然精度较高，但过程复杂。本文根据船舶航行时，导线在线束、线缆内随机运动的极限位置计算出导线最好、最差2种情况下的寄生参数值，利用感性—容性近似耦合方程求出相应的串扰耦合。

1 寄生参数最好、最差情况预测模型

单位长度互电感、互电容解析公式如式 (1)、式 (2)所示［5］:

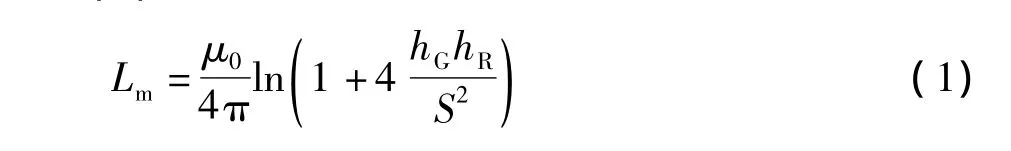
式中:Lm为导线A、B之间单位长度互电感;hG、hR为导线A、B与地之间的距离;S为导线A、B之间距离;μ0为真空磁导率。

式中:Cm为导线A、B之间单位长度互电容;εr为介质相对介电常数;εe为有效介电常数;ε0为真空介电常数;rA，rB为导线A、B的导体半径;ΔrA，ΔrB为导线A、B绝缘层厚度。

由公式 (1)和 (2)可知:当导线高度hG、hR最大，距离S最小时，互电感Lm和互电容Cm最大，是互电感和互电容的最差情况;当导线高度hG、hR最小，距离S最大时，互电感Lm和互电容Cm最小，是互电感和互电容的最好情况。hG、hR、S在最大、最小之间变化，Lm和Cm也在最好、最差情况之间动态变化。这就是寄生参数最好、最差情况预测原理。船舶内部线束如图1所示。

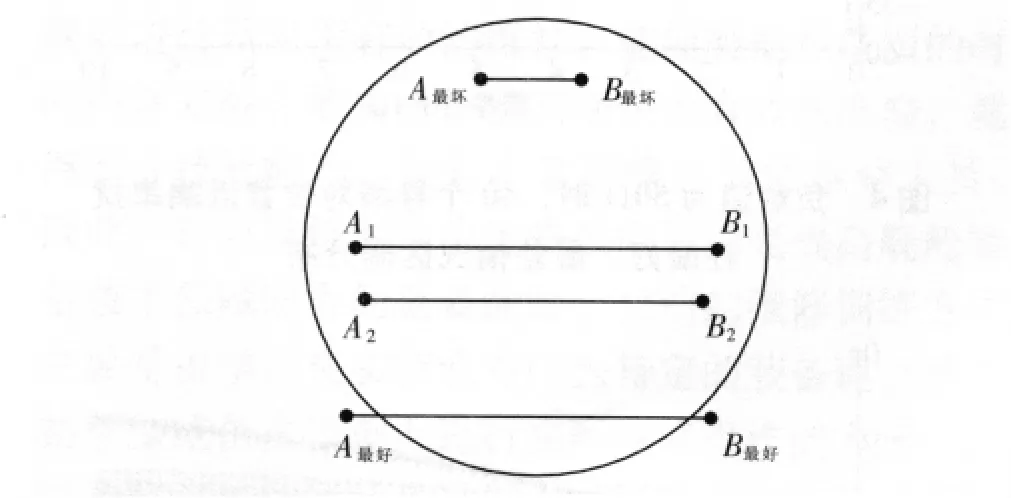
图1 线束内导线极限几何位置

设线束半径为R，线束内导线为同种导线，半径为r，线束中心距离地面高度为H。据式(1)、(2)可知，A、B高度 hG=hR=hmax=H+R－r，相互间距离S=2r时，互电感和互电容取得最大值，此时A、B外切，r=rA+ΔrA=rB+ΔrB。但外切能引起严重的邻近效应，对互电容的计算产生较大误差。基于此，A、B在最差情况下高度仍为hG=hR=hmax=H+R－r，但导线间距离S必须满足S＞2r的条件，以克服邻近效应的影响，S亦不能过大，否则互电感、互电容减小很多，最差情况失去意义。图2中，A最坏、B最坏为互电感和互电容最差情况位置。将 hG=hR=H+R－r代入式 (1)、(2)，得到互电感和互电容最差情况解析式为:

式中:r为导线半径;H为线束中心对地高度;R为线束半径。

因为线束截面为圆形，互电感和互电容的最好情况位置不易确定。据式 (1)和 (2)，最好情况位置应在低于A1B1，与地面平行的某个位置。设最好情况位置在A2B2。一般可用多元函数条件极值方法确定A2B2位置，但该方法繁琐、复杂。

简单起见可利用线束外两点A最好、B最好代替线束内互电感、互电容的最好情况位置。A最好点和B最好点高度为hG=hR=hmin=H－ (R－r)，相互距离S=2(R－r)，如图 (1)所示。据式 (1)、(2)可知，导线在A最好和B最好位置的互电感和互电容值小于线束内任意两点位置的互电感和互电容值。将hG=hR=hmin=H－(R－r)和S=2(R－r)代入式 (1)、(2)，可得互电容和互电感最好情况解析式为:

式中物理量含义见式 (2)、(3)。

假设线束半径R为4.5mm，导体半径rA为0.4mm，绝缘层相对介电常数εr为3.0，厚度ΔrA为0.6mm，导线半径 r=rA+ΔrA=1.0mm，线束中心距地面高度 H为25mm。A最坏、B最坏位置为A最坏(3.425，28.5)，B最坏(5.575，28.5)，导线间距离为2.15大于2倍导线半径。A最好、B最好位置为 A最好(1，21.5)，B最好(8，21.5)。将以上数据代入式 (4—6)得到 A最坏、B最坏位置最差情况互电感为 6.56×10－7H/m，互电容为 22.31×10－12F/m;A最好、B最好位置最好情况互电感为3.66×10－7H/m，互电容为7.70×10－12F/m。

随机在线束内选取40个导线对位置，使用EMC Studio仿真软件计算导线在这些位置的互电感、互电容，判断互电感和互电容是否在最好、最差情况区间内。图2为互电感在最好、最差情况区间内分布图，图3为互电容在最好、最差情况区间内分布图。从图2、图3看出，随机选择的40个导线对位置的互电感和互电容EMC Studio结果都在解析的互电感、互电容最好、最差情况区间内，说明寄生参数的最好、最差情况模型是有效的。

图2 线束内40个导线对位置单位长度互电感值在最好、最差情况区间分布情况

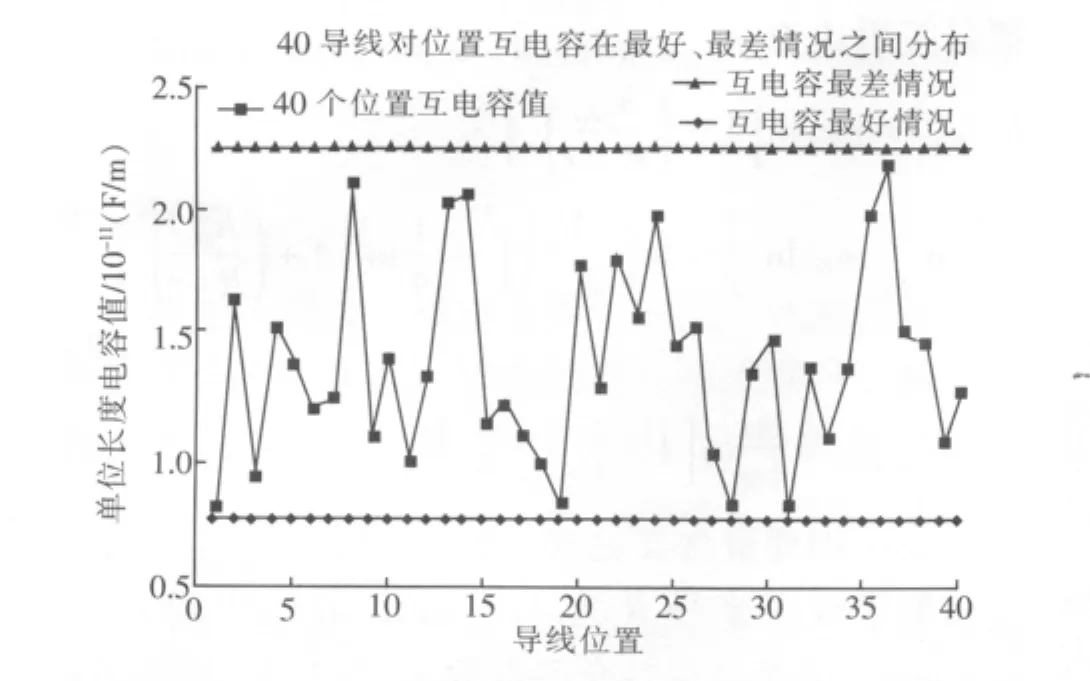
图3 线束内40个导线对位置单位长度互电容值在最好、最差情况区间分布情况

2 串扰的最好、最差情况预测模型

船舶航行时，线束互电感和互电容变化，电感性和电容性串扰耦合必然变化。其它参数不变，线束互电感、互电容为最差情况时，线束串扰亦为最差情况。此时线束近端串扰 (NEXT)耦合公式为:

同理，当线束互电感、互电容为最好情况时，线束串扰亦为最好情况。此时线束近端串扰耦合公式为:

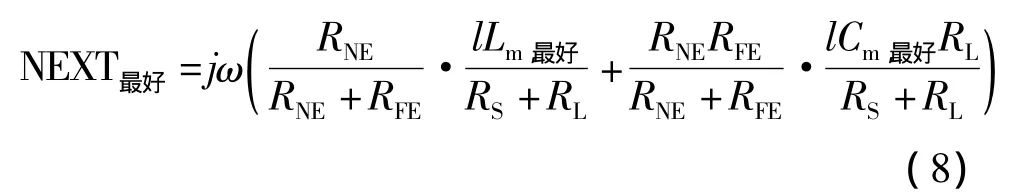
图4、图5是 RNE、RFE、RS、RL值均为50 Ω和1000 Ω时，线束内40个导线对位置的近端串扰在最好、最差情况区间分布情况。

图4 负载值为50Ω时，40个导线对位置近端串扰在最好、最差情况区间分布

图5 负载值为1000 Ω时，40个导线对位置近端串扰在最好、最差情况区间分布

从图4、图5可以看出，频率低于5MHz，随机选择的40个导线对的近端的EMC Studio结果都在解析的最好、最差情况区间内;频率高于5MHz，导线在一些位置点串扰值的EMC Studio结果低于最好情况值，其原因可能与频率增加，接收电路对发生电路的二次效应渐趋明显有关。

3 结束语

根据船舶航行时导线在线束内随机运动的极限几何位置，得到线束单位长度寄生参数和串扰的最大、最小值，即最好、最差情况值，以寄生参数和串扰的最大、最小区间估计寄生参数和串扰的动态变化。模型简单、实用，能够快速估计船舶线束寄生参数和串扰的动态变化，确保问题不被漏掉，且不需用复杂和昂贵的仿真软件和实验测量，这在缺少资金和完整几何、电气数据的船舶电磁兼容设计初期十分重要。

［1］Clayton R.Paul.电磁兼容导论 ［M］.北京:人民邮电出版社，2007.

［2］ Ajibola Ajayi，Philip Ingrey，Phillip Sewell，etc.Direct Computation of Statistical Variations in Electromagnetic Problems［J］.IEEE Transactions on Electromagnetic Compatibility.2008，50(2):325 –333.

［3］B.Cannas，A.F.，F.Maradei.Crosstalk Prediction in Twisted Bundles by a Neural Approach.［C］.Proceedings of the 3rd International Symposium＆Technical Exhibition on Electromagnetic Compatibility(EMC)2002.Beijing，P.R.China.2002:638 － 641.

［4］B.Cannas，A.Fanni，F.Maradei etc.Neural Networks to Statistically Simulate Crosstalk in Random Bundles［C］.Proceedings of the International Symposium on Electromagnetic Compatibility，September 9 －13，2002，Sorrento，Italy.

［5］王瑞宝.汽车线束寄生参数和串扰预测研究 ［D］.长春:吉林大学，2011.