规则波对弹性支承水平板冲击压力的概率分析
2013-05-17王国玉王永学
刘 明,任 冰,王国玉,王永学
(大连理工大学海岸和近海工程国家重点实验室,大连 116024)
规则波对弹性支承水平板冲击压力的概率分析
刘 明,任 冰,王国玉,王永学
(大连理工大学海岸和近海工程国家重点实验室,大连 116024)
通过模型试验研究了规则波对弹性支承水平板冲击压力峰值的概率分布。文中通过对不同组次的试验数据进行统计分析,首先给出了弹性支承与刚性支撑之间水平板波浪冲击压力历时曲线的各自特征;其次研究了弹性支承水平板波浪冲击压力峰值的超值概率分布及拟合曲线和参数;最后讨论了弹性支承刚度与威布尔分布三参数之间的关系。
波浪冲击;弹性支承;水平板;压力峰值;超值概率;威布尔分布
Biography:LIU Ming(1984-),male,doctor student.
顺岸式码头、海洋采油平台、海上栈桥等透空式结构物由于其上部结构水平面板高程设计不当或长时间使用引起结构整体沉降等原因致使结构物净空不足,面临波浪冲击的危险[1],波浪冲击作用所产生的极强的冲击荷载会引起建筑物的整个上部结构失稳或造成局部破坏[2]。以往的研究和工程实践表明在结构体净空不足的情况下,极强的波浪冲击荷载不是造成结构体损坏的直接原因,而结构体的弹性变形或振动引起的微裂纹经过长时间的积累才是造成混凝土结构和钢结构损坏的主要原因[3]。鉴于浅水资源的日渐枯竭,越来越多的弹性结构体如深水导管架平台(FP)、张力腿平台(TLP)和半潜式平台(SEMI)等在深水区域兴建起[4],海洋资源的开发由浅水向深水发展,结构体的整体刚度必然要从刚性逐渐向弹性变化[5],结构体的弹性响应对波浪冲击压力的影响也就变得越来越突出。
波浪冲击作用的研究始于20世纪60年代,关于小尺度水平圆柱的波浪冲击问题主要是采用半理论半经验的方法将波浪冲击力的表达式简化为Fs=0.5CsρDLU2,波浪冲击系数Cs主要通过试验来确定,其理论值为π[6]。目前国内外学者确定的Cs值比较分散,从1.0到7.79不等[7-11];由于最大冲击系数Cs的离散程度很大,因此在实际工程中的运用还存在着很大的限制。关于大尺度水平板冲击问题的研究,Wang等[12-17]基于一定的假设对波浪冲击力进行了理论分析并给出了波浪冲击压力的理论公式或经验公式;Goda等[18-23]分别给出了不同物理模型试验条件下的冲击力公式;Lai[24],Baarholm[25-26],王永学、任冰和李雪临[27-29]等人分别利用有限元法(FEM)、边界元法(BEM)和流体体积法(VOF)建立了求解波浪冲击压力的数值模型。
上述波浪冲击问题的研究成果基本假设结构体为刚性体,忽略了结构体的弹性振动或变形等现象对结构体或冲击压力的影响,距离实际的工程需要相差甚远。目前国内外学者对大尺度弹性水平板冲击问题的研究主要可以分别为以下三个方面:理论分析研究,Kva°lsvold 等[30-35],Haugen[36-38],Khabakhpasheva 等[39-40]等人分别基于相关假设通过单根梁模型法、三根梁模型法和正态模型法对弹性水平板结构的入水冲击问题进行了理论分析并给出了相关的理论结果;物理模型试验研究,Sulisz[3,41]对弹性支撑水平板的波浪冲击问题进行了试验研究,研究者认为波浪冲击所导致的振动是结构损坏的主要原因;Aarsnes[35,42],Kva°lsvold[32],Faltinsen[33]等人对弹性水平板的入水冲击问题进行了试验研究并给出了结构弹性响应与结构固有周期之间的关系;数值模拟研究,Kva°lsvold[30-32],Faltinsen[33],Khabakhpasheva[39],Korobkin[40]等人分别通过有限差分法(FDM)对弹性水平板的入水冲击问题进行了数值模拟研究并与相关理论研究进行了对比。
上述弹性结构体冲击问题的研究成果大多是针对入水冲击问题的情况,而对于实际工程中的弹性结构体,如海洋平台、海上栈桥等等,其上部结构的波浪冲击问题往往不能简化为入水冲击问题。目前对于弹性结构体的波浪冲击问题,国内外的研究尚无较大进展,国内的相关文献依然有限。因此为深入理解弹性支承透空式水平板在规则波作用下的冲击机理;了解不同刚度弹性支承水平板在波浪冲击下冲击压力的概率分布问题,弹性支承刚度对分布参数的影响情况;本文通过物理模型试验对弹性支承透空式水平板的波浪冲击问题进行了研究,并给出了本次试验范围内的相关结论。
1 试验设计
试验在大连理工大学海岸和近海工程国家重点实验室的溢油水槽中进行。水槽长22 m,宽0.8 m,高0.8 m,生波周期范围为0.5~3.0 s。水槽的一端配有大连理工大学海岸和近海工程国家重点实验室研制生产的DL-3型液压伺服不规则波造波机,由微机控制造波与数据采集处理。水槽的另一端装有消能装置,以减小和消除波浪反射的影响。模型放置在水槽的中后部,如图1所示。
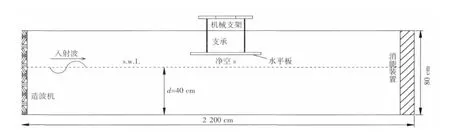
图1 试验设备示意图Fig.1 Sketch of experimental setup
试验模型设计以导管架式海洋平台为原型,结合实验室溢油水槽的尺寸和适当的试验比尺,经过适当简化后取水平板试验模型长76 cm,宽76 cm,厚1.2 cm;水平板总质量m=8.5 kg;平台桩腿用Φ=4.2 mm的白钢丝制作,一端固定于水槽上方的机械装置上,一端固定于试验模型上,将结构物模型悬吊于静水面以上,如图1所示;平台面板的整体刚度k可以通过调节桩腿高度来改变,结构物模型距离静水面的距离s(净空)可以通过顶部的机械装置来调节。

图2 模型压力传感器布置示意图Fig.2 Sketch of pressure transducers in the model
结构物模型迎浪面布置了2个水平压力传感器,底面布置了8个竖向压力传感器,其布置如图2所示。波浪冲击压力采用北京水利科学研究院生产的DS30型MD-14、32CH脉动压力测量系统测量,压力传感器的响应频率可达100 000 Hz(一个测点的最小采样间隔为0.000 01 s,10个测点的最小采样间隔为0.000 1 s),本次试验的采样间隔为1/512 s。
本文试验的入射波浪为规则波,试验水深d为40 cm;波高H分别为8.0 cm、10.0 cm和12.0 cm;波浪周期T分别为1.0 s、1.3 s和1.6 s;模型净空s分别为1.0 cm、2.0 cm和3.0 cm;试验模型根据支承刚度k的不同分为3个(Model-1、Model-2、和Model-3)。试验中通过测定模型的自振频率来推算模型的刚度(k=4π2f2m),详见表 1。

表1 模型的刚度k与自振频率fTab.1 The stiffness and free vibration frequency of the model
2 试验结果分析
2.1 波浪冲击压力历时曲线
试验中通过布置在平板模型底面的8个压力传感器和迎浪面的2个压力传感器,记录了各测点的冲击压力历时曲线。图3给出了不同试验模型下水平板迎面2号和底面5号测点的波浪冲击压力历时曲线,其横坐标为时间t,单位为s,纵坐标为冲击压力p(kPa),Px为水平冲击压力,Pz为竖向冲击压力。
从图3中可以明显看出,弹性支承与刚性支撑下水平板所受波浪冲击压力历时曲线的特征是一致的;首先,波浪冲击压力均具有明显的周期性,其周期与入射波浪周期一致;其次,在一个冲击周期内,波浪冲击压力均会出现不同的压力过程;最后,各个周期内的冲击压力幅值均具有很强的随机性;这与前人的研究[27,43]相一致。
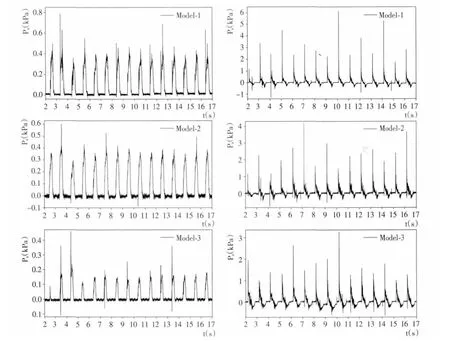
图3 规则波作用下水平板迎面2号和底面5号测点冲击压力历时曲线(T=1.0 s,H=12.0 cm,s=2.0 cm)Fig.3 Time series of regular wave impact pressure on the 2nd and 5th transducer of horizontal plate
2.2 波浪冲击压力峰值的超值概率
由于波浪冲击过程中最大冲击压力峰值的随机性很强,为得到弹性支承下水平板的最大冲击压力峰值的概率分布特征,本文对一个工况重复进行了50次试验,每次试验采样时间约为15倍的入射波周期。
试验数据分析中选取采样时间内8个竖向压力传感器中某瞬时的最大峰值作为竖向最大冲击压力峰值,取2个水平压力传感器中某瞬时的最大峰值作为水平最大冲击压力峰值。对同一组次试验可得到50个最大冲击压力峰值,记为一个样本。对该样本进行概率分析,确定结构物所受的最大波浪冲击压力峰值的超值概率分布曲线。
图4给出了不同试验模型下水平板最大冲击压力峰值的超值概率及威布尔分布的拟合曲线。其横坐标为样本中任意峰值p(kPa)与样本的平均值(kPa)的比值,记为p/,纵坐标为样本中任意给定的p/值在样本中的超值概率分布,记为FE(p/)。图中px(kPa)为水平冲击压力,pz(kPa)为竖向冲击压力(kPa)为水平方向的样本平均值(kPa)为竖直方向的样本平均值。
从图4中可以明显的看出,波浪最大冲击压力峰值的超值概率分布与三参数威布尔分布曲线的拟合很好,其相关系数R值均大于0.94。说明弹性支承水平板下波浪最大冲击压力峰值的超值概率分布是一种威布尔分布,如式(1)所示

式中:D为位置参数;L为尺度参数;M为形状参数。
威布尔分布的3个参数,位置参数D是曲线的起点,本文将其取为pmin/(pmin为样本中的最小冲击压力峰值);尺度参数L是一个整体的尺寸参数,并不影响曲线的基本形状,与样本的个体差异有关;形状参数M是威布尔分布中具有实质意义的参数,与分布曲线的型态有关,当形状参数M取不同值时,就会出现不同的分布型态,如M=3.5~3.6时近似为正态分布,M=1时为指数分布,M=2时为瑞利分布。

图4 规则波对弹性支承水平板冲击压力峰值的超值概率分布(T=1.0 s,H=12.0 cm,s=2.0 cm)Fig.4 Exceeding probability distribution of slamming pressure peak of regular wave impact on elastically supported horizontal deck
从图4中可以看出,威布尔分布的3个参数中位置参数D和尺度参数L与弹性支承刚度的变化关系不大,而形状参数M则随着弹性支承刚度的减小而逐渐减小,说明当弹性支承刚度较小时,威布尔分布曲线单调递减的速度减小,超值概率分布曲线变得较为平缓,波浪冲击压力峰值出现的概率将变得较大。
2.3 冲击压力峰值的韦布尔分布参数分析
图4中威布尔分布的位置参数D和尺度参数L之和(D+L)遵循着一定的变化规律,故表2和表3分别给出了竖向冲击压力峰值的威布尔分布参数与水平冲击压力峰值的威布尔分布参数值。
从表2中可以看出,在不同波浪条件和模型条件下竖向冲击压力峰值的威布尔分布参数D和L变化幅度不大,基本上在围绕一定值变化。位置参数D的变化范围为0.46~0.62,尺度参数L的变化范围为0.46~0.63;且位置参数D和尺度参数L之和(D+L)基本为定值1.0,其变化范围为1.03~1.09。
从表3中可以看出水平冲击压力峰值的威布尔参数变化规律基本与竖向冲击压力峰值分布参数相同。位置参数D的变化范围为0.47~0.78,尺度参数L的变化范围为0.25~0.58;且位置参数D和尺度参数L之和(D+L)基本为定值1.0,其变化范围为1.02~1.08。
从表2和表3中可以明显地看出,竖向冲击压力峰值威布尔分布的位置参数D基本小于水平的位置参数,尺度参数L基本大于水平的位置参数,说明竖向冲击压力峰值的样本数据较水平冲击压力峰值的样本数据分散;位置参数D和尺度参数L之和(D+L)随着弹性支承刚度的减小而有所增加,个别组次除外,说明弹性支承刚度越小水平板波浪冲击压力峰值出现的概率就越大。
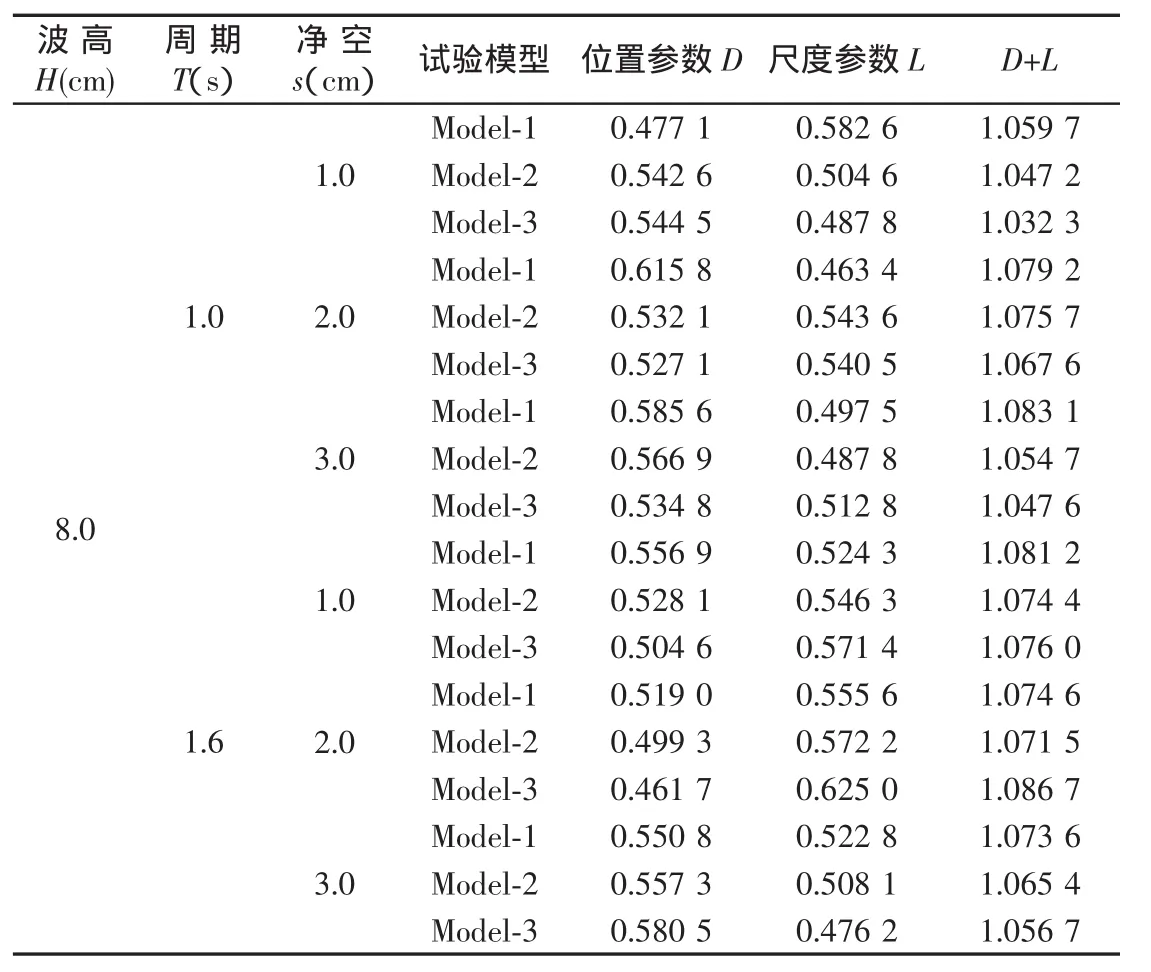
表2 竖向冲击压力威布尔分布的参数(D,L)的拟合值Tab.2 Parameter fitting value of Weibull distribution from vertical slamming
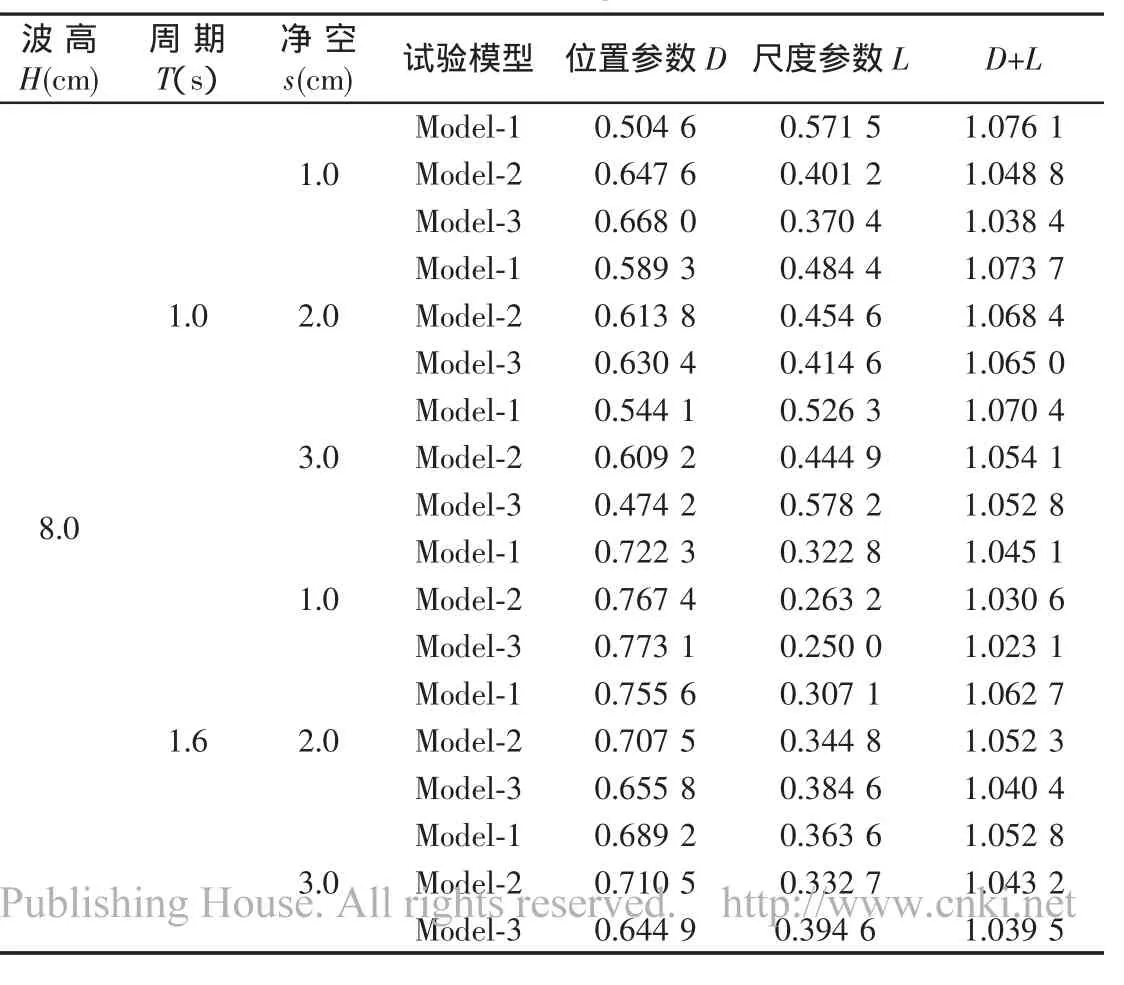
表3 水平冲击压力威布尔分布的参数(D,L)的拟合值Tab.3 Parameter fitting value of Weibull distribution from horizontal slamming
2.4 波浪冲击压力峰值的威布尔分布
从图4中可以明显看出,水平板波浪冲击压力峰值的超值概率分布符合三参数的威布尔分布,由表2和表3可知尺度参数L=1-D=1-pmin。故式(1)可以写成
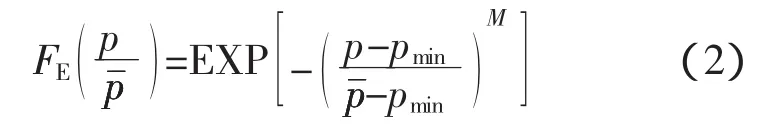
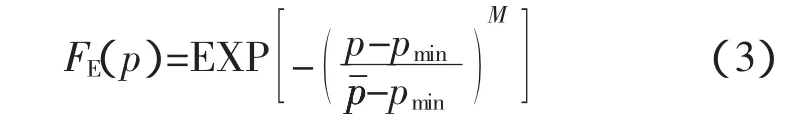

3 结论
本文对规则波浪作用下弹性支承水平板的冲击作用进行了物理模型试验研究,在不同波浪条件和模型条件下,对水平板迎面和底面的波浪冲击压力峰值进行了统计和分析,所得结论主要如下:
(1)弹性支承与刚性支撑下水平板波浪冲击压力历时曲线的各自特征是一致的,均具有明显的周期性,不同的阶段性和很强的随机性。
(2)弹性支承水平板波浪冲击压力峰值的超值概率分布符合三参数的威布尔(Weibull)分布

式中:pmin为位置参数;-pmin为尺度参数;M为形状参数。
(3)位置参数和尺度参数之和约为一定值1.0,形状参数则随着弹性支承刚度的减小而逐渐减小,说明当弹性支承刚度越小,水平板波浪冲击压力峰值出现的概率越大。
(4)规则波对弹性支承水平板的冲击作用下,波浪冲击过程中任意峰值p等于样本均值的概率为P{p=}=e-1=36.79%。
[1]任冰,丁兆强,王永学,等.单向波对浪溅区三维结构物冲击作用的试验研究[C]//中国海洋工程学会.第十三届中国海洋(岸)工程学术讨论会论文集.南京:海洋出版社,2007.
[2]Kaplan P,Silbert M N.Impact forces on platform horizontal members in the splash zone[C]//OTC.Proceeding of the 8th Annual Offshore Technology Conference.Houston,Texas,USA:OTC,1976.
[3]Sulisz W,Wilde P,Wisniewski M.Wave impact on elastically supported horizontal deck [J].Journal of Fluids and Structures,2005,21(3):305-319.
[4]杨建民,肖龙飞,盛振邦.海洋工程水动力学试验研究[M].上海:上海交通大学出版社,2008.
[5]唐友刚.海洋工程结构动力学[M].天津:天津大学出版社,2008.
[6]Chan E S.Extreme wave action on large horizontal cylinders located above still water level[C]//ISOPE.Proceedings of the 3rd International Offshore and Polar Engineering Conference.Singapore:ISOPE,1993.
[7]Dalton C,Nash J M.Wave slam on horizontal members of an offshore platform[C]//OTC.Proceeding of the 8th Annual Offshore Technology Conference.Houston,Texas,USA:OTC,1976.
[8]Miller B L.Wave slamming loads on horizontal circular elements of offshore structures [J].Journal Royal Institute Naval Architects,1978,3:169-175.
[9]Faltinsen O M,Kjaerland O,Nφttveit A,et al.Water impact loads and dynamic response of horizontal circular cylinders in offshore structures[C]//OTC.Proceedings of the 9th Annual Offshore Technology Conference.Houston,Texas,USA:OTC,1977.
[10]Sarpkaya T.Wave impact loads on cylinders[C]//OTC.Proceedings of the 10th Annual Offshore Technology Conference.Houston,Texas,USA:OTC,1978.
[11]Isaacson M,Prasad S.Wave slamming on a horizontal circular cylinder[C]//ISOPE.Proceedings of the 3rd International Offshore and Polar Engineering Conference Singapore:ISOPE,1993.
[12]Wang H.Water wave pressure on horizontal plates[J].Journal of the Hydraulics Division,1970,96(10):1 997-2 017.
[13] French J A.Wave uplift pressures on horizontal platforms[C]//ASCE.Proceedings of the Speciality Conference:Civil Engineering in Oceans IV.San Francisco,California,USA:ASCE,1979.
[14]Kaplan P.Wave impact force on offshore structures:Re-examination and new interpretations[C]//OTC.Proceedings of the 24th Annual Offshore Technology Conference.USA:OTC,1992.
[15]Bea R G,Xu T,Stear J,er al.Wave forces on decks of offshore platforms[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1999,125(3):136-144.
[16]Baarholm R,Faltinsen O M.Experimental and theoretical studies of wave impact on an idealized platform deck[C]//ICHD.Proceedings of the 4th International Conference on Hydrodynamics.Japan:ICHD 2000 Local Organizing Committee,2000.
[17]Baarholm R.A simple numerical method for evaluation of water impact loads on decks of large-volume offshore platforms[C]//OMAE.Proceedings of the 24th International Conference on Offshore Mechanics and Arctic Engineering.Halkidiki,Greece:OMAE,2005.
[18]Goda Y.Wave forces on structures[J].Summer Seminar on Hydraulics,JSCE,1967:B34..
[19]Elghamry O A.Uplift forces on platform decks[C]//OTC.Proceedings of the 3rd Annual Offshore Technology Conference.Houston,Texas,USA:OTC,1971.
[20]过达,蔡保华.透空式建筑物面板上波浪上托力的计算[J].河海大学学报,1980,8(1):14-33.
GUO D,CAI B H.The computation of wave uplift force on the deck of an open sea pillar quay[J].Journal of Ho Hai University,1980,8(1):14-33.
[21]Wang Y X,Liu M Z,Ren B.Experimental study of wave slamming[C]//OMAE.Proceedings of the 17th International Conference on Offshore Mechanics and Arctic Engineering.Lisbon,Portugal:OMAE,1998.
[22]REN B,WANG Y X.Spectral analysis of irregular wave impact on the structure in splash zone[C]//OMAE.Proceedings of the 17th International Conference on Offshore Mechanics and Arctic Engineering.Oslo,Norway:OMAE,2002.
[23]周益人,陈国平.透空式水平板波浪上托力冲击压强试验研究[J].海洋工程,2004,22(3):30-40.
ZHOU Y R,CHEN G P.An experimental study on uplift impact pressure of waves on a horizontal plate of an open wharf[J].The Ocean Engineering,2004,22(3):30-40.
[24]Lai C P,Lee J J.Interaction of finite amplitude waves with platforms or docks[J].Journal of Waterway,Port,Coastal and Ocean Engineering,1987,115(1):19-39.
[25]Baarholm R,Faltinsen O M.A boundary-element method for salving water impact on a platform deck[C]//OMAE.Proceedings of the 20th Offshore and Arctic Engineering Conference.New York,USA:OMAE,2001.
[26]Baarholm R,Faltinsen O M.Wave impact underneath horizontal decks[J].Journal of Marine Science and Technology,2004,9(1):1-13.
[27]任冰.随机波浪对不同接岸型式码头上部结构的冲击作用研究[D].大连:大连理工大学,2003.
[28]Ren B,Wang Y X.Numerical simulation of random wave slamming on structures in the splash zone[J].Ocean Engineering,2004,31:547-560.
[29]李雪临.波浪冲击过程的流场变化特性研究[D].大连:大连理工大学,2009.
[33]Faltinsen O M,Kvlsvold J,Aarsnes J V.Wave impact on a horizontal elastic plate[J].Journal of Marine Science and Technology,1997,2(2):87-100.
[34] Faltinsen O M.The effect of hydroelasticity on ship slamming[J].Philosophical Transactions of the Royal Society A:Mathematical,Physical and Engineering Sciences,1997,355(1 724):575-591.
[35]Faltinsen O M.Hydroelastic slamming[J].Journal of Marine Science and Technology,2000,5(2):49-65.
[36]Haugen E M,Faltinsen O M,Aarsnes J V.Application of theoretical and experimental studies of wave impact to wetdeck slamming[C]//FAST.Proceeding of the 4th International Conference on Fast Sea Transportation.Sydney:FAST,1997.
[37]Haugen E M.Hydroelastic analysis of slamming on stiffened plates with application to catamaran wetdeck[D].Trondheim:Norwegian University of Science and Technology,1999.
[38]Haugen E M,Faltinsen O M.Theoretical studies of wetdeck slamming and comparisons with full scale measurements[C]//FAST.Proceedings of the 5th International Conference on Fast Sea Transportation.USA:FAST,1999.
[39]Khabakhpasheva T I,Korobkin A A.Wave impact on elastic plates[C]//iwwfb.Proceeding of the 21st International Workshop on Water Waves and Floating Bodies.France:iwwwfb,1997.
[40]Korobkin A A,Khabakhpasheva T I.Regular wave impact onto an elastic plate[J].Journal of Engineering Mathematics,2006,55:127-150.
[41]Sulisz W,Paprota M.Vibrations of a horizontal deck due to extreme wave impact[C]//JOINT.Proceeding of the Chinese-German Joint Symposium on Hydraulic and Ocean Engineering.Germany:JOINT,2008.
[42]Stenius I.Hydroelasticity in marine hull bottom panels-modeling and characterization[D].Stockholm:KTH(Royal Institute of Technology),2009.
[43]丁兆强.波浪对透空式三维结构物的冲击作用研究[D].大连:大连理工大学,2009.
Probability analysis on slamming pressure of regular wave impact on elastically supported horizontal deck
LIU Ming,REN Bing,WANG Guo-yu,WANG Yong-xue
(State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian116024,China)
Based on the regular wave slamming on the elastically supported horizontal deck,the experimental investigation of the exceeding probability distribution of slamming pressure peak was presented.The experimental data obtained from different model test cases were analyzed.First,the characteristics of the time series of wave impact on elastically and rigidly supported horizontal deck were given.Then,the fitting curves of exceeding probability distribution of the slamming pressure peak and parameter values were studied.Finally,the relationship between the stiffness of elastically supported and the parameters of Weibull distribution was discussed.
wave impact;elastically supported;horizontal deck;pressure peak;exceeding probability;Weibull distribution
TV 131.6;P 751
A
1005-8443(2013)06-0493-08
2013-01-04;
2013-04-09
国家自然科学基金资助项目(50879009);国家自然科学基金创新研究群体项目(50921001)
刘明(1984-),男,陕西省富平人,博士研究生,主要从事波浪与结构物相互作用的研究。
