基于因子分析的各省份城镇居民消费结构研究

袁 云

（武汉理工大学 理学院，湖北 武汉 430070）

随着居民生活水平的不断提高以及经济发展方式的转变，居民的消费结构也在逐步转变。“十二五”期间，国内经济将主要以内需为主，最终体现出消费率提升和内需消费市场的活跃。因此，居民的消费水平是内需的主要来源，消费结构也会影响到各地区经济的持续稳定快速发展以及经济结构的突出转变，在“十二五”开局之年，看清楚各地区居民的消费水平结构，合理进行规划，才能推动经济发展和经济结构向合理方式的转变［1］。

本文在这个大前提下，为了减小各个省份在诸多方面的差异，选取各地区城镇居民家庭全年人均的消费性支出作为研究数据，根据《中国统计年鉴-2012》［2］得到 2011 年第一季度的统计数据结果，运用因子分析法对全国居民消费结构进行分析。

1 因子分析模型及原理

因子分析是一种数据简化的技术，它的概念是由英国著名统计学家、心理学家Charles Spearman在1904年提出的。因子分析本身是用于处理多维随机变量在线性变换下分量相关问题，它主要通过求协方差阵或相关系数阵的特征值和特征向量，按指定的贡献率求集中原来随机变量主要信息的、相互无关的主因子［3-4］。我们利用数学模型表示因子分析的主要过程。

设有 X1，X2，…，Xmm个变量，由因子分析的要求可知，假设这些变量已经标准化（均值为0，标准差为1），且假设m个变量可以由n个因子 f1，f2，…，fn表示为线性组合，即

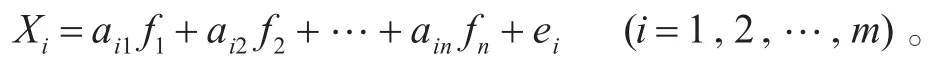
上式为因子分析的数学模型，利用矩阵形式则表示为

其中X为可观测的n维变量向量，它的每一个分量表示一个指标或变量；F称为公共因子，是相互独立且不可观测的理论变量；e称为特殊因子，各特殊因子之间以及特殊因子与所有公共因子之间都是相互独立的［5］，它表示原始变量中不能由因子解释的部分，均值为0；矩阵A为旋转成分矩阵，其元素 aij(i=1，2，…，m，j=1，2，…，n)称为旋转成分，它的绝对值越大（aij≤1），表明 Xi与Fj的相依赖程度越大，或者称Fj对于 Xi的载荷量越大，故矩阵A也称为因子载荷矩阵。

2 实证分析

2.1 数据采集

本文利用2011年第一季度城镇居民全年消费性支出的资料，采用因子分析法提取影响居民生活的公共因素，对我国居民消费水平进行全面综合评价。选取8个指标分别为食品（X1）、衣着（X2）、居住（X3）、家庭设备用品及服务（X4）、医疗保健（X5）、交通和通讯（X6）、教育文化娱乐服务（X7）、其他商品和服务（X8）。

2.2 判断数据是否适合做因子分析

KMO（Kaiser-Meyer-Olkin）统计量主要用于研究变量之间的偏相关性，它用来比较各变量之间的简单相关和偏相关的大小，取值范围在0～1之间。如果各变量之间存在内在关系，则由于计算偏相关时控制其他因素将同时控制潜在的变量，这样会导致偏相关系数远远小于简单相关系数，此时KMO统计量接近1，做因子分析效果最佳。一般认为，当KMO为0.9以上表示非常适合做因子分析，0.8表示适合做因子分析，0.7表示一般，0.6表示不太适合，0.5以下则不适合做因子分析。

Bartlett球形检验主要用于检验相关矩阵是不是单位矩阵，即各变量是不是各自独立。Bartlett球形检验参考值见表1。

表1 KMO和Bartlett的检验

从表1可以看出，KMO=0.801＞0.5，Bartlett球形检验的伴随概率为0，表示拒绝各变量是独立的假设，两种检验的结果均表示各变量间存在相关性，比较适合做因子分析。8项指标的公因子方差提取值见表2。

表2 公因子方差

从表2可以看出，每一个变量的公因子方差均在0.5以上，且均大于0.8，可知被提取的公因子对各变量的解释能力是非常强的，说明3个公因子能够较好地客观反映原变量的大部分信息。

2.3 运用因子分析法对数据进行分析

本文用SPSS19.0统计软件对数据进行统计分析，相关系数矩阵的特征值以及贡献率如表3所示。

表3 相关系数矩阵的特征值、贡献率

由表3，根据因子分析特征值大于1的原则筛选出2个公因子，但是它们的累积贡献率仅为79.475%，所以我们选3个公因子来解释。3个公因子的累积贡献率为90.731%，即第一个公因子可以解释变量的65.161%，第二个公因子可以解释变量的14.315%，第三个公因子可以解释变量的11.255%，说明3个公因子可以较充分地解释各变量，数据信息保留充分，具有良好的统计意义。

用这3个公因子建立旋转成分矩阵，将建立的旋转成分矩阵进行方差最大正交旋转。旋转成分矩阵以及成分得分系数矩阵见表4和表5。

表4 旋转成分矩阵

表5 成分得分系数矩阵

通过四次方的最大旋转之后，得到8个变量在3个公因子上的新的因子负荷。结果显示，食品、交通和通讯、教育文化娱乐服务、家庭设备用品及服务在因子1上有较高的载荷，称因子1为发展消费因子［6］；衣着、居住、其他商品和服务在因子2上有较高的载荷，称因子2为经济消费因子；由于医疗保健在因子3上有较高的载荷，称因子3为健康消费因子。

从成分得分系数矩阵表可以得到旋转后的因子得分函数：

其中FAC_1是因子1得分，FAC_2是因子2得分，FAC_3是因子3得分。

2.4 结果分析

居民消费结构与经济发展水平密切相关。各因子的旋转成分矩阵反映了该因子与原始变量的关系及解释能力。根据旋转后的因子得分函数得到各省份因子得分如图1所示。

图1 各省份因子得分

从图1看出，贵州省因子1得分最低，说明贵州省整体发展水平最低，辽宁省因子1得分最高，其次为天津，说明它们整体发展水平较高。发达地区的消费结构更偏重于服务业［7］。比如辽宁省的教育文化娱乐服务的支出位居全国首位，这就促进了辽宁省的教育业、文化业以及娱乐服务业的发展。消费结构也会进一步影响经济的快速发展趋势，高消费也将带动这片区域中相关产业的发展。

对于因子2，江苏省得分最高，依次为天津和重庆。说明这3个省经济发展比较快，居民生活相对舒适。而西藏自治区和甘肃省得分比较低，说明经济发展比较落后，居民生活相对艰苦。由此可见，经济的发展水平对于消费结构的影响很大，这是由于经济发展水平影响了居民的消费观念、产业结构、生活方式等。

江苏省因子3的得分高达3.17249，表明江苏省居民在健康方面的消费比较高，说明医疗改革让居民看病更加方便、省心，带动了居民在健康方面的消费。

3 结语

将因子分析法有效地应用于居民消费结构变化中，可以将居民消费结构清晰地表现出来，便于不同省份在充分了解省内居民消费结构的情况下，制定下一步发展的规划，引导居民消费向更加合理的结构方向发展［8］，从而不断地提高居民的收入水平，进一步提高我国居民的消费水平，最终有效地促进我国经济的发展，加快居民进入小康的步伐。

对于大部分省市，在加快产业结构调整过程中应考虑居民的消费特点，适应消费市场的需求，提供更多满足消费者所需求的商品，来促进消费的提高和改善人民的生活水平，同时，引导消费向合理化发展，尽量避免畸形消费的产生。

［1］高莉菁.全国各省份城镇居民消费结构的聚类分析［J］.中国证券期货，2011（5）：127.

［2］国家统计局.中国统计年鉴-2012［M］.北京：中国统计出版社，2012.

［3］李雪，王莉华.基于聚类和因子分析的农村居民消费结构实证研究［J］.辽宁石油化工大学学报，2008，28（2）：93-96.

［4］罗应婷，杨钰娟.SPSS统计分析从基础到实践［M］.北京：电子工业出版社，2010：281-286.

［5］周亚，俞海山.浙江居民消费结构变动的因子分析［J］.商场现代化，2011（14）：86-87.

［6］周发明，杨婧.基于ELES模型的中国城乡居民消费结构实证研究［J］.中国科技论文在线，2010，9（3）：84-85.

［7］陈捷.中国城镇居民消费结构变化的定量分析［J］.统计与决策，2003（1）：46-47.

［8］邓菲.因子分析在我国城镇居民消费结构变动的应用［J］.科技经济市场，2008（11）：45-46.