正确选择统计判别法剔除异常值

2013-05-14孙培强

计量技术 2013年11期

孙培强

(西安计量技术研究院，西安 710068)

0 引言

异常值又称离群值，是指在对一个被测量重复观测所获得的若干观测结果中，出现了与其它值偏离较远并且不符合统计规律的个别值，他们可能来自不同的总体，或属于意外、偶然的测量错误，也称为存在着“粗大误差”。造成异常值的原因很多，如：震动、冲击、电源变化和电磁干扰等意外的环境条件变化；人为的读数或者记录错误；仪器内部的偶发故障等。

如果一系列测量数据中存在异常值，必然会歪曲测量的结果。若能将该值剔除不用，便能使测量结果更符合客观情况；有些情况下，一组正确测量值的分散性，本来客观地反映了实际测量的随即波动性，若人为地丢掉一些偏离较远但不属于异常值的数据，会使得到的所谓分散性很小，实际上却是虚假的。因为，以后在相同条件下再次测量时原来的正常分散性还会显现出来，因此必须正确的判别和剔除异常值。

在测量过程中，如果遇到记错、读错、仪器突然跳动和突然震动等异常情况，这些已知原因的异常值，应该随时发现，随时剔除，这就是物理判别法。如果仅仅是怀疑而不能确定某个值是异常值时，可采用统计判别法进行判别。

1 判别异常值常用的统计方法

1.1 拉依达准则

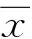
1.2 格拉布斯准则

设在一组重复观测结果xi中，其残差υi最大者为可疑值xd，在给定的置信概率为p=0.99或p=0.95，也就是显著水平a=l-p=0.01或0.05时，如果满足下述公式，可以判定xd为异常值。

式中，G(a,n)为与显著水平a和重复观测次数n有关的格拉布斯临界值(见表1)。

表1 格拉布斯准则的临界值G(a ,n)表

1.3 狄克逊准则

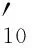
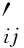
否则没有异常值。

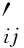
表2 狄克逊检验的临界值D(a ,n)表

3 三种判别准则的应用与比较

实例：在测量过程中得到10个值，按从小到大排列为：8.75，8.76，8.78，8.79，8.80，8.82，8.83，8.91，8.92，9.13。

观测值实验标准偏差s=0.114

3.1 根据拉依达准则计算

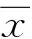
3.2 根据格拉布斯准则计算

按p=0.95,即a=l-p=0.05，n=10,查表得G(0.05,10)=2.176

按p=0.99,即a=l-p=0.01，n=10,查表得G(0.01,10)=2.410

3.3 根据狄克逊准则计算

观测值个数n=10用下面公式

3.4 三种判别准则的比较

拉依达准则和格拉布斯准则得出的结论截然相反，原因在于观测值的个数并不大，用贝塞尔公式求得的仅是理论上的实验标准偏差的估计值。当n比较小时，求得的实验标准偏差值比较大。此时，若依照拉依达准则的3s做判断依据，并不可靠，当以3s为界限时，即使有粗大误差也发现不了；而格拉布斯准则在理论上给出了严格而具体的判定标准，所以两者之间的得出的结论截然相反。

格拉布斯准则和狄克逊准则在理论上都给出了严格而具体的判定标准，但他们对同一组数据的判定结果也有差异。一般情况下，格拉布斯准则比狄克逊准则严格。狄克逊准则不使用实验标准偏差来判定异常值，而是用极差比来判定异常值，并且要求不同的测量次数应用不同的极差比公式计算，公式多，不宜记忆。格拉布斯准则有唯一的公式，方法简便，易于掌握，而且可靠。格拉布斯准则适用于单个异常值，而狄克逊准则可以多次剔除异常值。

格拉布斯准则和狄克逊准则对测量次数有要求，测量次数大于50次不能使用格拉布斯准则，测量次数大于30次不能使用狄克逊准则，而拉依达准则对测量次数没有限制。

所以当测量次数n>50的情况下，拉依达准则较简便实用；在测量次数3