基于MATLAB的平面度误差评定及可视化的GUI设计*
2013-05-14阮小丽
阮小丽
(南通市产品质量监督检验所, 南通 226005)
0 引言
零件加工过程中,由于各种因素影响,加工出来的零件总存在各种形式的加工误差,这就需要通过测定来确定这些误差的性质和大小。产品质量监督检验人员在借助于各种检测手段或方法检测产品质量的过程中,首先明确质量标准要求,然后选用便捷准确的测试方法和采用合理的测试手段来检验产品,得到质量特征值或数据,再将测试的数据结果经过整理同质量标准要求作比较,确定产品质量是否合格[1]。
随着MATLAB 软件功能的日益完善,MATLAB是当今科研领域最常用的应用软件之一,它具有强大的矩阵计算、符号运算和数据可视化的功能。在MATLAB软件中有一个模块叫图形用户界面(GUI/ Graphical User Interface),它是指采用图形方式显示的计算机操作用户界面[2]。这种面向客户的系统工程设计其目的是优化产品的性能,使操作更人性化,减轻使用者的认知负担,使其更适合用户的操作需求。
平面度误差是机械加工中常见而又重要的检测项目。许多学者在平面度误差的评定方面进行了研究,提出了多种平面度误差近似优化评定方法。如最大直线度法、对角线法、三点法、最小二乘法、最小区域法、遗传算法等[3~8],目的在于建立满足最小条件的理想包容区域,以实现准确评定。
本文介绍用MATLAB通用软件评定平面度误差及可视化方法,具有很好的实用性。
1 平面度误差的评定方法
根据中华人民共和国国家标准GB/T 11337—2004规定[9],平面度误差的定义为实际平面t对其理想平面的变动量,而理想平面的位置应符合最小条件。平面度误差值为用平面度最小包容区域的宽度f表示的数值,见图1。应用于三坐标机的平面度评定方法主要是最小包容区域法和最小二乘法,评定的实质是求解评定基面的参数。
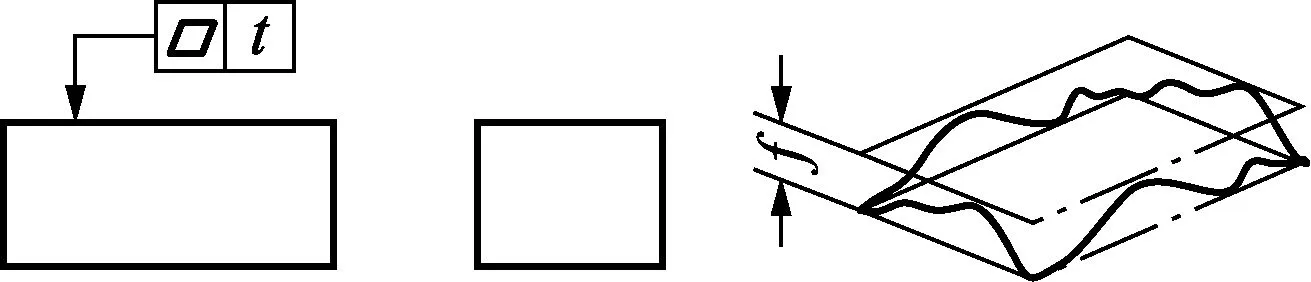
图1 平面度误差示意图
1.1 最小二乘法求平面度误差
平面在空间直角坐标系中的一般方程为
Ax+By+Cz+D=0 (C≠0)
(1)
式(1)可以写成
(2)
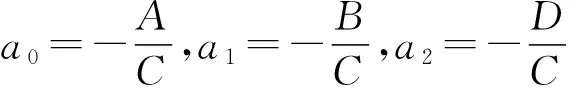
则式(2)可以改写成
z=a0x+a1y+a2
(3)
根据GB/T 11337—2004规定[9]5.3.1测量布点的方法测量n个点(n≥3):
(xi,yi,zi),i=0,1,…,n-1
要用点(xi,yi,zi),i=0,1,…,n-1拟合计算上述平面方程,则使S最小。
(4)
要使得S最小,应满足
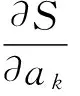
即
(5)
有
(6)
或
(7)
解上述线形方程组,得:a0,a1,a2,从而得到基准平面方程。
再将各测点相应的坐标(xi,yi,zi),i=0,1,…,n-1代入平面方程,即可得对应的z方向坐标值,所以平面度误差为
δ=max(zi-z)-min(zi-z)
(8)
1.2 最小区域法求平面度误差
根据平面的标准方程,用最小包容区域法推导出计算公式,平面的一般方程为式(1)所示。
三坐标测得n(n>3)个点的坐标为(xi,yi,zi),i=0,1,…,n-1,各点到平面的距离为
(9)
根据各点距离构造的下列函数即为最小包容区域平面应该满足的方程
δ=[di]max-[di]min
(10)
式中,[di]max、[di]min分别为di中的最大值和最小值。
1.3 遗传算法求平面度误差
遗传算法是基于自然选择,在计算机上模拟生物进化机制的寻优搜索算法。遗传算法的操作是模拟生物基因的操作,它的任务就是根据个体的适应度对其施加一定的操作,从而实现优胜劣汰的进化过程。从优化搜索的角度而言,遗传操作可使问题的解逐渐地优化,逼近最优解。遗传操作包括以下三个基本遗传算子:选择、交叉和变异。选择和交叉基本上完成了遗传算法的大部分搜索功能,变异增加了遗传算法找到接近最优解的能力。在后面的程序设计中,运用遗传算法第一步先选择出最好的10个解,第二步进行交叉处理,第三步再进行变异处理,最后处理得到平面度误差。
2 平面度误差可视化处理
MATLAB提供的从插值到数据图示一系列的函数,为软件的开发提供了极大方便。程序中使用的数据插值方法有四种:立方插值法(cubic)、V4插值法(V4)、线性插值法(linear)、最近点插值法(nearest)。利用这四种数据插值法将某组20个测点数据可视化处理,如图2~5所示。其中,图2的立方插值和图3的V4插值生成的图形比较平滑,而图4的线性插值和图5的最近点插值所生成的图形在零阶和一阶不连续,从而显示的图形没有那么平滑。就其算法原理, 线性插值、 立方插值和最近点插值都基于数据Delannay三角化,从图中可以直观地感受到平面的实际形貌。在编译的可执行程序中添加了显示精度设置,显示精度越小,显示的网格越小。
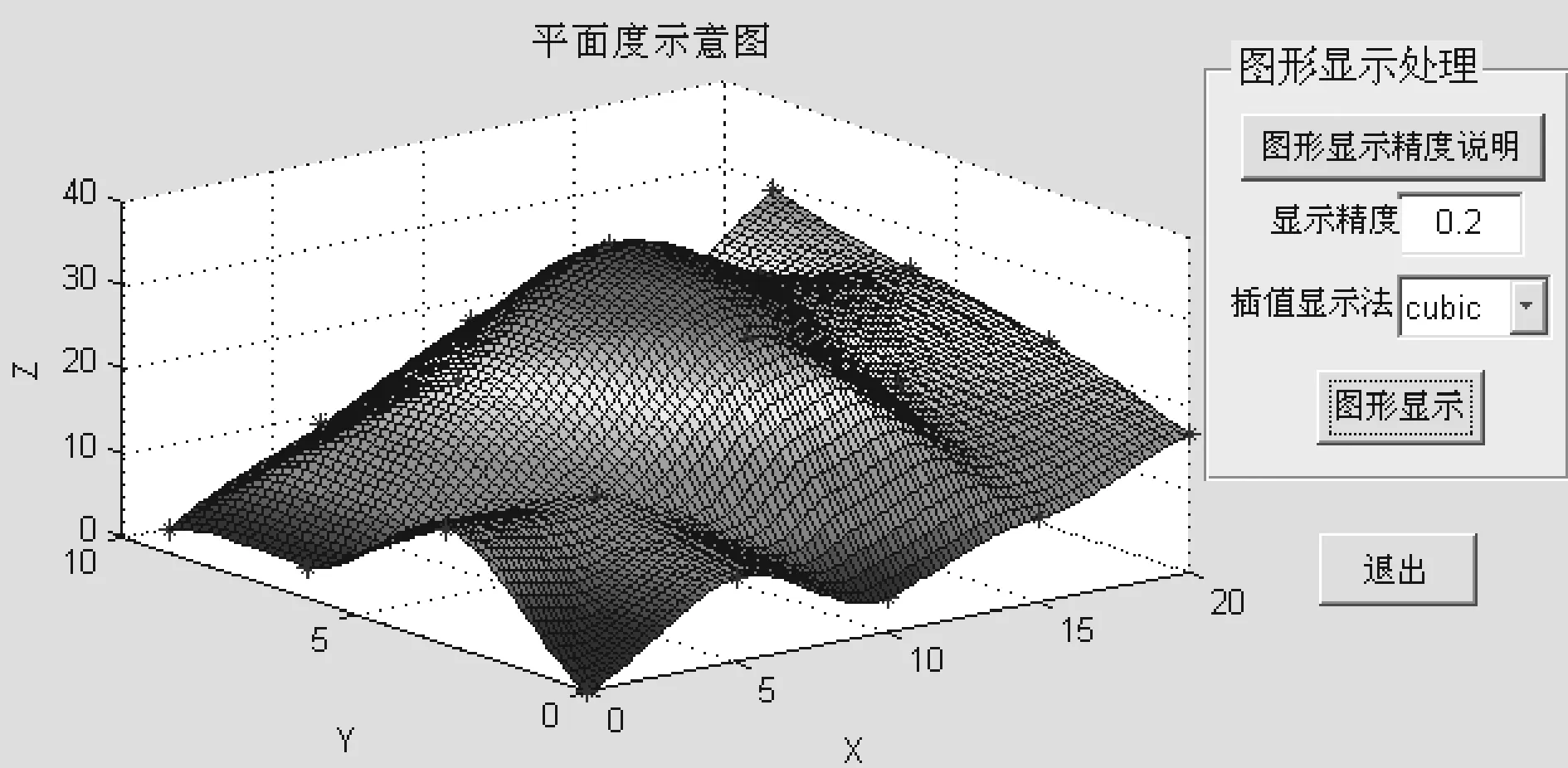
图2 立方插值
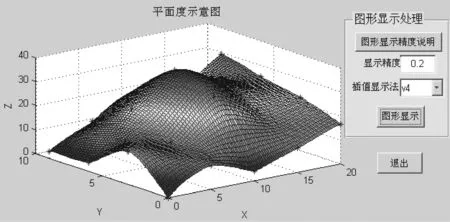
图3 V4插值
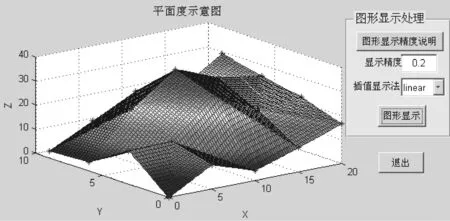
图4 线性插值
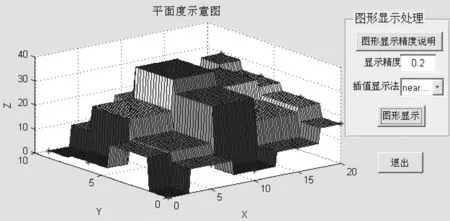
图5 最近点插值
3 平面度误差评定的GUI程序实现

图6 程序主要界面
程序的主要界面如图6所示,主要有三大部分:测量数据导入处理区域、平面度评定区域和平面三维可视化区域。测量数据导入处理区域可以实现测量数据的导入以及处理输出保存。如果和一些自动测量设备连接起来,例如运用GLOBAL FX777型三坐标测量机自动扫描完成被测平面的数据点采样,采样点的坐标数据以.TXT 格式的文件导出,将测量结果导入处理,这样可以实现快速评定平面度误差及可视化显示。平面度评定区域可以采用三种不同方法评定平面度误差,再通过对比选择最优结果。程序中实现平面度不同方法评定的流程如图7所示。
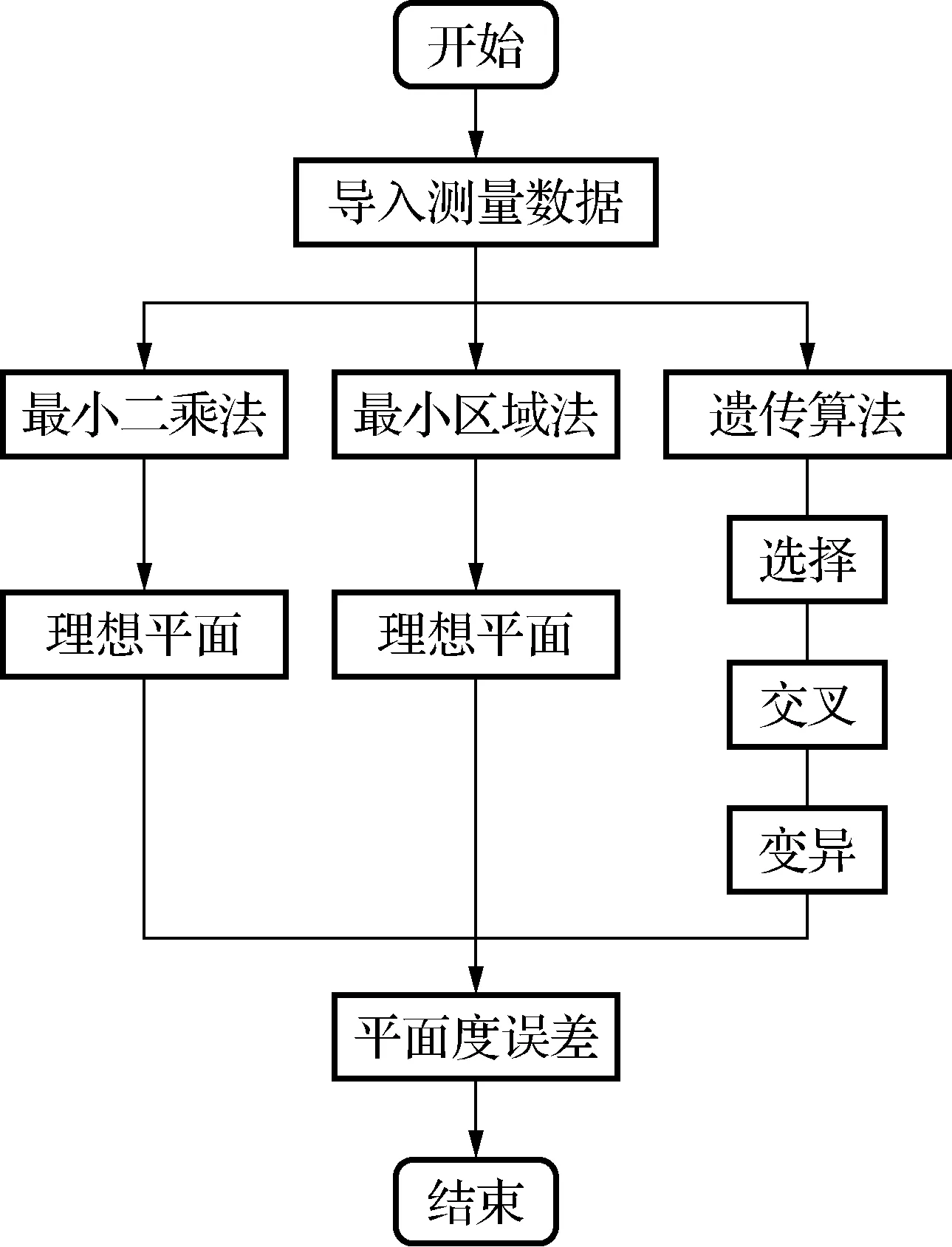
图7 程序平面度评定流程
程序中运用3种方法对测量数据处理,评定出平面度误差。
1)最小二乘法
根据前面的评定方法数学模型的理论阐述,能够顺利编译程序实现最小二乘法的平面度误差评定。
2)最小区域法
按照文献[10] JJG 117—2005平板检定规程的标准规定,符合“最小条件原则”平面度的判别准则:三角形准则、交叉准则和直线准则。三角形准则:一个最低(高)点的投影位于由三个等值最高(低)点所组成的三角形内(凸三角形和凹三角形);交叉准则:两个等值最低(高)点的投影位于两个等值最高(低)点连线的两侧;直线准则:一个最低(高)点的投影位于两个等值最高(低)点的连线上。程序中运用了一些判断语句,再根据以上准则判断包容平面是否包容了所有的点,最后计算给出平面度误差的评定结果。
3)遗传算法
此方法有三个基本遗传算子:选择、交叉和变异。运用MATLAB实现遗传算法对平面度的评定,这方面的文献资料比较少,为此下面给出程序的主要部分。
for m=1:100 %迭代100次循环
for i=1:100
F=(a(i)*A(:,1)+b(i)*A(:,2)+c(i)-A(:,3))./(a(i)^2+b(i)^2+1)^0.5;
D(i)=max(F)-min(F);
end
[X,Y]=sort(D);
for i=1:10%选择出10个最好的解
AA(i)=a(Y(i));
BB(i)=b(Y(i));
CC(i)=c(Y(i));
end
…
k=11;
for i=1:9 %交叉
for j=i+1:10
if rand>0.5
AA(k)=a(i);
AA(k+1)=a(j);
AB(k)=b(i);
AB(k+1)=b(j);
AC(k)=c(j);
AC(k+1)=c(i);
…
k=97; %变异
AA(k)=a(1).*1.05;
AB(k)=b(1);
AC(k)=c(1);
k=k+1;
AA(k)=a(2);
AB(k)=b(2).*1.05;
AC(k)=c(2);
k=k+1;
AA(k)=a(3);
AB(k)=b(3);
AC(k)=c(3).*1.05;
…
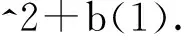
E=max(D)-min(D); %平面度误差评定
4)GUI程序的准确性验证
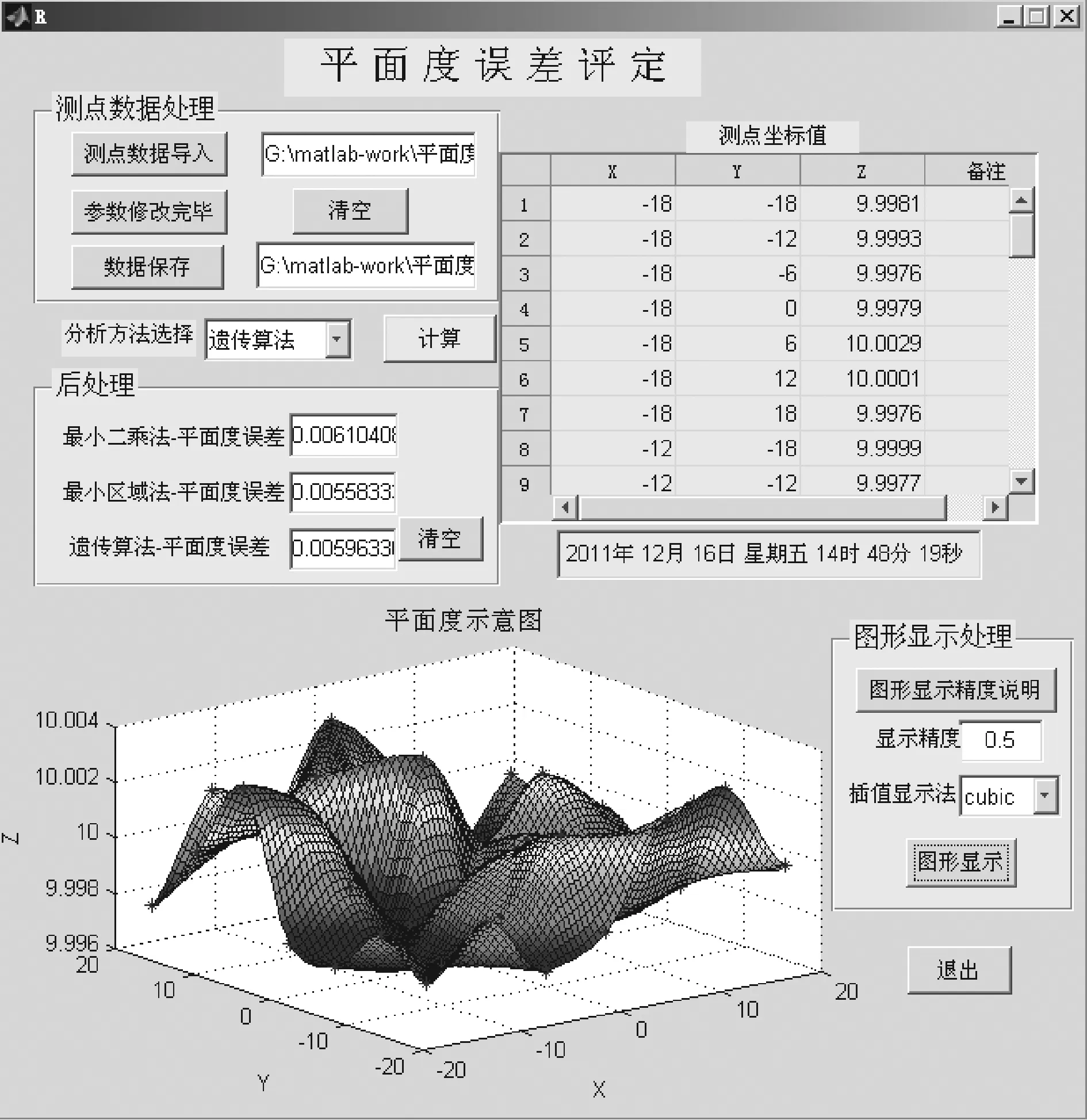
图8 平面度误差评定结果显示
为了比较最小二乘法、最小包容区域法和遗传算法的平面度误差评定精度,同时也为了验证笔者编译的可执行程序的准确性,对给定平面度误差进行测量与评定。程序导入参考文献[11]里的一组数据如表1所示,通过运行编译的可执行程序后,计算结果如图8所示。参考文献[11]中运用了最小二乘法和最小区域法,最小二乘法评定平面度误差为0.0061mm,最小区域法评定平面度误差为0.0056mm。
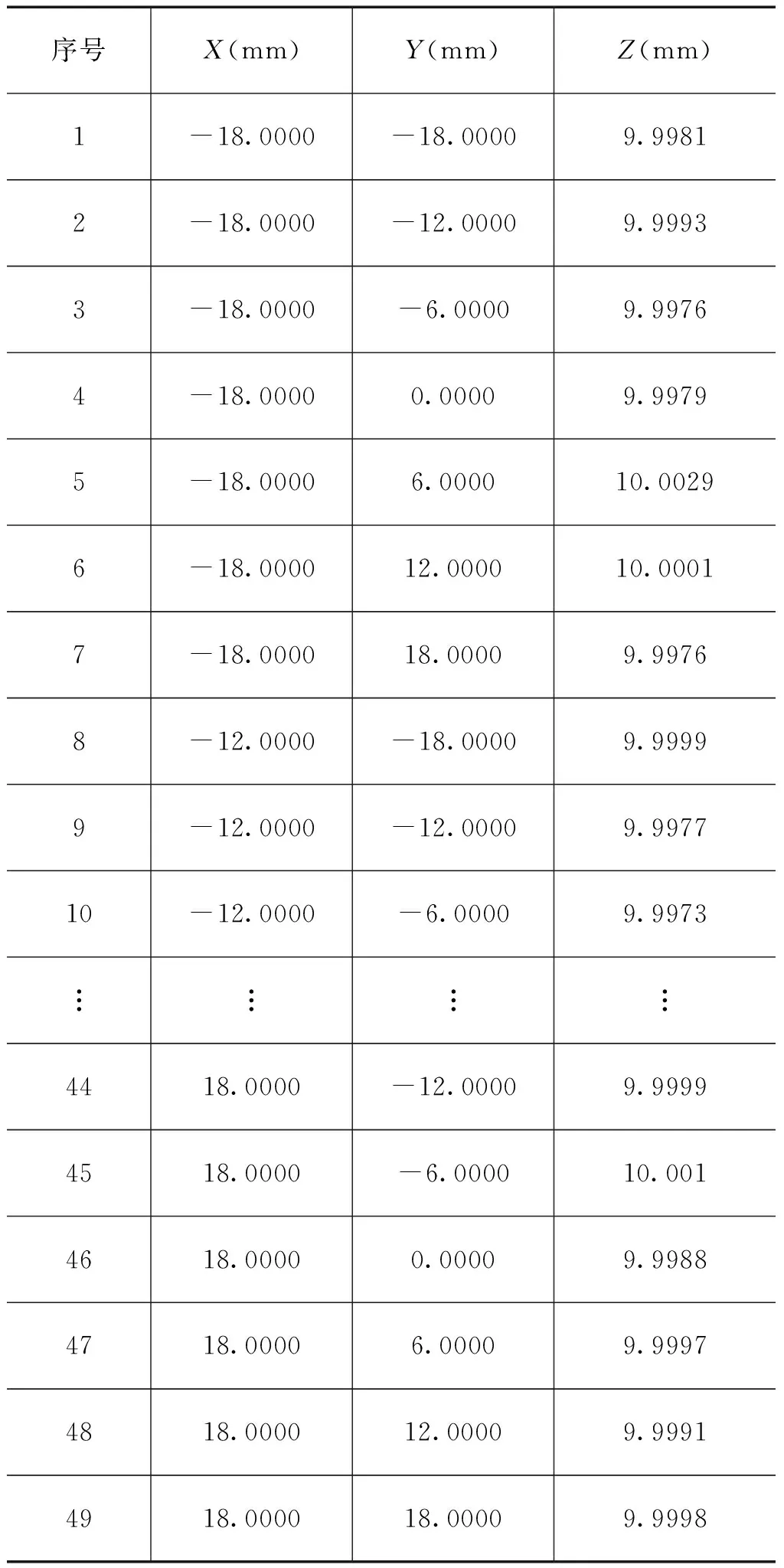
表1测量点坐标数据
从图8中可见,本程序最小二乘法评定平面度误差为0.0061mm,最小区域法评定平面度误差为0.00558mm,遗传算法评定平面度误差为0.00596mm。对比充分说明了本程序分析结果的准确性,而且在3种评定方法中,最小区域法评定平面度误差时产生的误差最小,精确度最高。
本文开发的平面度误差评定的可执行程序,用户操作人员可以通过简单操作GUI界面,能够实现从界面上导入实验测量数据,选择所需要的评定方法后,便可直接得出平面度误差值输出到计算机屏幕指定的位置。还可以通过点击绘图显示按钮绘出直观形象的三维模拟图形。本软件设计的界面友好操作简单、求解速度很快且测量结果准确。
4 结论
平面度误差的几种常用评定方法中,只有最小区域法是国家标准规定的方法, 采用最小区域法评定时产生的误差最小,精确度最高。本文基于MATLAB开发的用户界面可执行程序,可以快速评定平面度误差以及可视化三维显示。这样有效提高了平面度误差检测效率,从一定程度上降低检测成本,对工程上的加工工艺分析也有很大的实际意义。
[1] 梁子午.检验工实用技术手册[M].南京:江苏科学技术出版社,2004
[2] 张琨,毕靖,丛滨.MATLAB 7.6从入门到精通[M].北京:电子工业出版社,2009
[3] 刘永超,陈明.形位误差的进化算法[J].计量学报,2001,22(1):18-22
[4] 岳武陵,吴勇.平面度和直线度误差的快速评定-增量算法[J].计量学报,2008,29(2)120-123
[5] Samuel G L,Shunmugam M S.Evaluation of straightness and flatness errors using computational geometric techniques[J].Computer-Aided Design,1999,31(13):829-843
[6] 薛小强.平面度误差的精确最小域解[J].机械设计与制造工程,2002,31(5)82-83
[7] Zhu X Y,Ding H.Flatness tolerance evaluation:an approximate minimum zone solution[J].Computer-Aided Design,2002,34:655-664
[8] Lee M K.A new convex-hull based approach to evaluating flatness tolerance[J].Computer-Aided Design,1997,29(12):861-868
[9] 中华人民共和国国家质量监督检验检疫总局.GB/T 11337—2004平面度误差检测[M].2004
[10] 国家质量监督检验检疫总局.JJG117—2005平板检定规程[M].中国计量出版社,2005
[11] 陈永鹏.基于MATLAB优化工具箱的机械产品形状误差评定系统研究[D].四川大学硕士学位论文,2003
