模拟谐振子算法在求解整数规划问题中的应用

姚明

（广东石油化工学院 计算机科学与技术系，广东 茂名 525000）

整数规划作为规划论的一个分支，是运筹学中的一个重要内容。整数规划问题广泛应用于工程领域与管理领域，如资源管理、生产调度、可靠性优化、目标分配、资本预算、股票分析、超大规模集成电路设计等[1-2]。

对于变量规模较小的整数规划问题，传统的求解方法有分支定界法、割平面法和隐枚举法等。但对于较大规模的问题，传统方法的计算非常耗时且结果常不能令人满意，如经常采用的方法是把用线性规划方法所求得的非整数解进行取整处理，而这在实际工作中所得到的解可能不是原问题的可行解或整数最优解。参考文献[3]在传统的分支定界法的基础上，提出了新的切割与分支算法进行求解，但由于在分支过程中采用的是经典的分支定界算法，故其效率仍受到分支准则的影响。近年来，许多学者应用遗传算法、模拟退火算法、粒子群优化算法、蚁群优化算法等方法求解整数规划问题[1-2，4]，取得了一定的效果，但问题规模较大时，在收敛的最优性和收敛速度方面仍有改进的必要。

模拟谐振子 SHO （Simulated Harmonic Oscillator）算法是近来提出的新的智能算法，目前已在解决旅行商问题、多项目调度问题时表现出了良好的效果[5-6]，但在其他领域的应用尚待研究和实践。本文将其应用于求解整数规划问题，通过设定振幅、初始步长、基态步长，确定差解接受规则、步长变化规则，控制各阶段的最大计算次数和解无变化次数的上限，以及在不同阶段使用不同的新解产生方法，使全局寻优与局部寻优较好地结合。测试结果表明了该算法应用于求解整数规划问题，当问题规模较大时具有高质量的搜索效率和精度。

1 SHO算法简介

SHO算法是由模拟自然谐振子运动的物理规律演化而来的一种通用的随机搜索算法。简谐振动系统中，弹簧质点在由端点运动到平衡点的过程中，其位置状态与势能状态一一对应。由于质点的运动是连续的，故其一定会经过系统的每个位置状态。对应地，系统的整个势能空间也将被遍历。如果将质点的位置状态对应于优化问题中的某个解状态，则理论上通过遍历质点位置状态就可以遍历优化问题的解空间，从而求得最优解。

在简谐振动系统中，弹簧质点处于平衡点时弹性势能最小（其值为0），在任意一个端点时弹性势能最大为系统总能量。可根据质点到平衡点的距离，将系统划分为多个能量等级。设振幅为A，某个能级处质点离平衡点的相对位移为x，系统势能被划分为A个等级，可以证明，在弹簧质点与平衡点的距离成等差数列形式变化的情况下，简谐振动系统的势能能级以递减的方式进行；另外，从量子物理的角度看谐振子即微观振动，当谐振子系统位于能量最低的基态时，波函数为高斯函数，此时可认为解将会以高斯分布方式出现[5]。由此可知，弹簧质点离平衡点越近，能级差越小；当算法系统的最终目标达到系统基态时，最有可能找到最优解。

算法分为初始化过程、经典简谐振动过程和在基态附近的量子简谐振动过程。对于一个计算问题的求解，算法首先在解空间以一定的次数查找端点和振源即近似的最差解和最优解，获得系统的近似最大势能。然后以基态步长为分界线，步长大于基态步长时为全局寻优阶段，对应于经典谐振子的振动。此阶段，算法在解空间随机搜索近似最优解，并采用接受规则对差解进行取舍，这样可使邻域解在局部山峰间平行跳跃，从而有效控制算法全局搜索的随意性并避免陷入局部搜索的陷阱。步长小于基态步长时为局部寻优阶段，对应于量子谐振子的振动，此时系统总体处于平衡态附近的量子振动状态，算法在解空间不会再有大的跳跃，对差解采用直接抛弃的策略，完成在基态附近向最优解的趋近。算法的基本步骤见参考文献[5]。

2 求解整数规划的SHO算法

整数规划问题可描述为[1]：

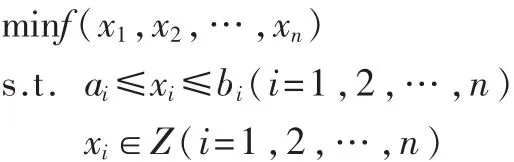
其中 Z 为整数空间，ai，bi（i＝1，2，…，n）为整数，li=bi-ai+1为xi的可能取的个数。每个变量取一个值就构成一个解。

SHO算法作为一种通用的智能算法，其应用于求解整数规划问题的特定领域时，在算法参数初始化、新解产生方法以及差解接受准则等方面需要有针对性地进行设置和定义。

2.1 算法参数初始化

SHO算法在初始化阶段需要设置振幅、初始步长和基态步长，确定步长变化规则以及确定谐振子端点和振源。其中，初始步长用于划分问题的能级并对应能级的最大处，其值代表着整个势能空间范围；基态步长代表某一较低的低能能级，其值代表着从基态到基态步长间能级总和；一个步长对应一个能级差，其变化可以为不规则跳跃，也可以逐步衰减（衰减方式的选择依赖于具体问题）。对于此阶段的求解整数规划问题，振幅应选取为某个变量的取值范围，初始步长的取值为振幅的倍数（倍数的大小与变量的规模和取值范围有关），基态步长取正整数1为宜。谐振子端点与振源通过一定次数的随机取解粗略确定（计算过程中最大的目标函数值对应的解为端点，最小的目标函数值对应的解为振源）。

2.2 新解产生方法

SHO算法的随机性主要体现在新解的产生上。求解目的、搜索策略以及新解的搜索邻域不同，产生新解的方法也不同。新解产生的方法对算法的效率与精度有较大的影响。产生新解的方法很多，SHO算法使用的方法有：均匀随机法、2交换（2-opt）法、两两随机交换法、随机插入法[5]等。对于求解整数规划问题，这些新解产生方法并不适用，需要重新设计。在解的生成上，利用随机函数产生新解是一种常用的方法，但是要得到高精度的解则需要很大的计算次数，特别是当变量规模较大时。在求解整数规划问题的新解产生方法的设计中，初始化阶段以及全局寻优的前期阶段使用了利用随机函数产生新解的方法；当步长L＝2时，设计了通过利用随机函数确定当前最小解的某个分量并对其值分别作减3、增3、减 2、增 2的扰动产生新解的方法，该方法可以在全局搜索的后期加快收敛速度并提高精度；当步长L＝1时，设计了通过利用随机函数确定当前最小解的某个分量并对其值分别作减1、增1扰动产生新解的方法，该方法适宜于基态时的局部寻优。通过测试对比，设计的这些新解产生方法，比较适合整数规划问题的求解。

2.3 差解接受规则

差解接受规则是算法的核心，可控制算法的收敛方向。由于初始步长L0的值代表着整个势能空间范围，基态步长LS的值代表着近似基态能级，又因为简谐振动过程中势能与距离的平方成正比，因此可用表示近似基态能级占整个势能的比例。假定s为当前近似最优解，s′为通过新解产生方法得到的另一解，则 f（s）为当前解对应的势能（其可近似为基态），f（s′）为新状态的势能，Δf＝f（s′）-f（s）可近似看成是新解势能与基态的能级差；再假定 End 为端点，则 f（End）-f（s）可近似为整个势能空间范围，可看成是新解与整个势能的比例。差解接受规则定义如下：

差解接受规则表明，当新解与整个势能的比例小于近似基态能级占整个势能的比例（或者说当新解相对势能在近似基态能级范围内）时，则接受新解（即使新解比当前解差），因为此时新解比旧解在能级上更低，符合算法寻找系统基态的目标要求。

2.4 算法步骤

求解整数规划问题的SHO算法的步骤设计如下：

（1）设定振幅A的值为某个变量的取值范围的长度、初始步长L0的值为振幅的倍数、基态步长LS的值为1，步长变化规则采用逐步递减的方式（通过L0递减实现）。同时，分别设定在确定振源和端点、步长 L∈[Ls，L0]阶段、L＝2 以及 L＝1 时求解的最大计算次数和解无变化次数的上限。

（2）利用随机函数产生新解 s，以目标函数值 f（s）最大的为端点 End，最小的为振源 Init。如果未达到此阶段设定的最大计算次数或解无变化次数的上限，则继续步骤（2）的操作。

（3）利用随机函数产生一个新解 s′，计算Δf＝f （s′）-f （s）。 若 Δf≤0， 或 Δf＞0 且≥0，则接受并记忆s′为当前解。如果未达到此阶段设定的最大计算次数或解无变化次数的上限，则 L0递减，在 L0≥LS条件下继续全局寻优；其中，当时L0＝2，新解通过利用随机函数确定当前最小解的某个分量并对其值分别作减3、增 3、减 2、增 2的扰动产生。

（4）当步长 L＝1时，通过利用随机函数确定当前最小解的某个分量并对其值分别作减1、增1扰动产生新解；若Δf≤0，则接受新解 s′为当前解。如果未达到此阶段设定的最大计算次数或解无变化次数的上限，继续局部寻优；否则，输出当前解为近似最优解，算法结束。

3 实例计算

[1]中测试粒子群优化算法求解整数规划所用的2个函数为例进行实例计算并对比。这些函数的全局最优点都是 xi＝0，fi（x）＝0。 另外，还将 f2（x）按与参考文献[2]的设置进行计算对比。

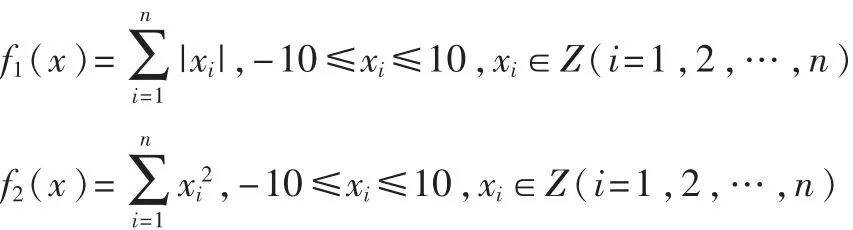
算法采用Java语言编程实现，开发工具为Eclipse IDE for Java Developers （Version：Indigo Service Release 1），运行环境为 Java（TM）SE Runtime Environment（build 1.7.0_07-b10）。设振幅 A＝21，初始步长 L0为 A的 n倍，基态步长LS＝1，步长通过L0递减的方式实现变化。以寻找到全局最优点为收敛标准。规定最大迭代次数为10 000次，否则称为不收敛。其中，确定振源和端点阶段最大计算次数为 200，控制解无变化次数的上限为 100；L∈[Ls，L0]阶段最大求解次数为500，控制解无变化次数的上限为200；L＝2阶段最大计算次数为 500，控制解无变化次数的上限为200；L＝1阶段控制解无变化次数的上限为2 000。另外，在将 f2（x）按参考文献[2]的设置进行计算时，修改 f2（x）变量取值范围为-100≤xi≤100，并相应设振幅A＝201。对函数在维数为 15、20、30时的各种情况，算法均运行20次。其结果及对比如表1所示。

表1 f1（x）、f2（x）计算结果

表1中“－”表示该种情况，算法不完全收敛，该项指标无法统计。表1显示出本文所设计的应用于整数规划问题的SHO算法在收敛的最优性和收敛速度方面均具有较好的性能，特别是当变量规模较大时，而且算法的稳定性较好，维数与变量取值区间的变化对计算结果所造成的波动不大。

对于变量规模较大的整数规划问题的求解，传统方法存在计算耗时与误差大的问题，而一些智能计算方法在收敛的最优性和收敛速度方面也存在不足。本文在SHO算法的基础上，设计了针对整数规划问题求解的SHO算法并进行实验。从实验结果及对比可以看出，SHO算法巧妙地将简谐振动思想应用于求解复杂问题，将全局搜索与局部搜索进行了较完美的结合，具有较高的解质量，并且算法的时间代价小，应用是可行的。

参考文献

[1]高尚，杨静宇.群智能算法及其应用[M].北京：中国水利水电出版社，2006.

[2]谭瑛，高慧敏，曾建潮.求解整数规划问题的微粒群算法[J].系统工程理论与实践，2004，24（5）：126-129.

[3]高培旺.整数线性规划的切割与分支算法[J].计算机工程与设计，2010，31（12）：2930-2932.

[4]杨荣华，刘建华.量子粒子群算法求解整数规划的方法[J].科学技术与工程，2011，33（11）：8195-8198.

[5]王鹏.云计算的关键技术与应用实例[M].北京：人民邮电出版社，2010.

[6]倪霖，段超，钟辉.基于模拟谐振子算法的多项目调度[J].计算机应用，2011，31（9）：2559-2562.