变压器式可控电抗器静态无功功率双向控制原理研究
2013-05-12段力勇王承民亚历山大洛夫
段力勇,王承民,亚历山大洛夫·戈·尼
(1.广东省电力设计研究院,广东广州 510000;2.上海交通大学电气工程系,上海 200240;3.俄罗斯圣彼得堡国立技术大学,俄罗斯圣彼得堡 197183)
在电力系统中,无功功率的平衡对于保证电网安全、可靠、经济运行极为重要,对于高电压、长距离输电线路更是如此。由于传统并联电抗器SR(Shunt Reactor)的功率不能够自动连续平滑调节,故不能很好地满足超高压长距离输电网无功平衡的需要。而对于静止无功补偿器SVC(Static Var Compensator),由于其技术复杂、造价昂贵、维护困难而没有得到大量使用。磁饱和式可控电抗器MCR(Magnetically Controllable Reactor)具有功率自动连续平滑调节的特点,近年来被广泛地研究和应用[1-4],但是MCR具有谐波含量高,响应速度慢的缺点。
20世纪70年代,BBC公司研制了一种可控并联电抗器[5],与MCR相比具有响应速度快的优势,但是由于其谐波含量高和功率损耗大等缺点而停止开发和生产。针对此BBC产品的不足,俄罗斯学者在20世纪末提出了变压器式可控电抗器CSRT[6],2001年俄罗斯圣彼得堡国立技术大学电力电子设备教研室成功研制了世界上第一台可控变压器式电抗器(CSRT),并且在印度投入了运行(400 kV,50 MV·A)[7],其不但具有MCR的优点,还克服了BBC可控电控器的不足,CSRT不仅可以用于电网的无功控制,而且由于响应速度快,也可以用于电网过电压限制和用作快速消弧线圈,可应用于负荷功率变化大的线路中,起到稳定和调整电压的作用。近年来,CSRT作为柔性交流输电系统家族中的重要成员,由于具有诸多优点而被广泛研究[8-10]。
在现有CSRT的研究中,通常是通过调整控制绕组中晶闸管的导通角来控制电抗器的等值电抗,从而达到调整无功功率的目的,对电抗器无功功率的控制主要是针对感性的无功功率;补偿绕组的功能是为了消除谐波、特别是3次以及其倍数谐波的影响。本文通过分析CSRT的等效电路和工作方式,在其基础上提出一种无功功率双向控制的补偿原理,不仅能在轻载时吸收线路中的剩余无功,还可以在其重载时补偿线路中所需要的无功以支撑电压的稳定,实现双向补偿的功能[11-16]。
1 CSRT的构成及其等效电路
CSRT相当于具有高短路阻抗的三绕组变压器,如图1所示。

图1 CSRT原理图和CSRT等效电路图Fig.1 CSRT schematics and CSRT equivalent circuit diagram
变压器一次绕组接入电网,二次绕组(控制绕组)串接晶闸管控制模块,三次绕组(补偿绕组)内并联接入3,5,7次LC滤波器。
滤波器由串联的电容器和电感线圈组成,选择其参数时应使得在相应高次谐波发生谐振,故:
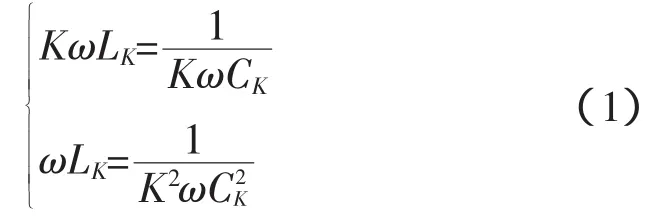
式中,K为高次谐波次序号。则在工频电压下,各次滤波器的等效电抗值为

显然,由于K>1,滤波器等效电抗为负值,则其等效阻抗具有容抗特性。由此可见,此控制电抗器不仅可以吸收轻载输电线路的剩余无功,还可以通过改变滤波器电容的参数来实现对重载输电线路提供所需的补偿无功功率。CSRT在工频电压下的等效电路图见图1(b),其中

式中,X12,X13,X23为不同绕组短路时CSRT的等效电抗(角标1对应系统绕组,2为控制绕组,3为补偿绕组,其中角标第二个数字表示对应绕组短路时)。
通过在一次绕组和二次绕组之间装设第三补偿绕组,其短路电抗参数则具有以下关系(不考虑补偿绕组的厚度)

式中,δ为位置系数,其值变化范围从0.5到0.8,受补偿线圈的装设位置的影响。
2 CSRT工作原理及参数计算
2.1 工作原理
先分析一下当晶闸管触发角分别为90°和180°时的工作状况。当触发角为180°时二次绕组相当于开路,容性电流(ICRa)t通过一次系统绕组传递到电力系统,其值
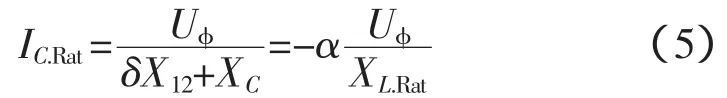
式中,XL.Rat为控制补偿器必需的额定等效电抗(在感性工作方式下)为额定容性功率相对于额定感性功率的比值。由此可以得到所需要的等效容抗值XC

当晶闸管触发角为90°的情况(相当于二次绕组在短路状态)时,在系统绕组中将通过额定感性电流为
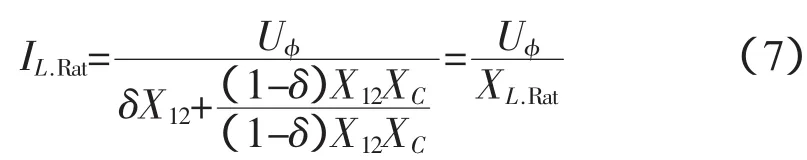
由此可以得到感性工作方式下的额定电抗值
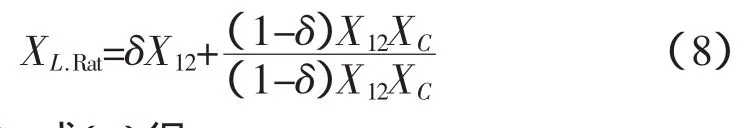
由式(6)、式(8)得

方程的解为
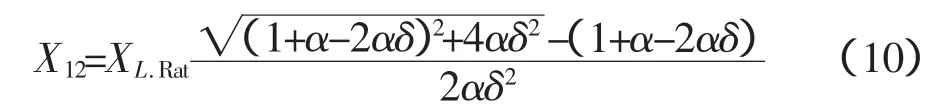
再将此结果带入式(6)得到所需要的XC

2.2 参数计算
接下来确定滤波器电容参数α=IC.Rat/IL.Rat,以确保所需关系,利用式(11)。根据文献[10],滤波器等效的无功电抗由以下关系确定
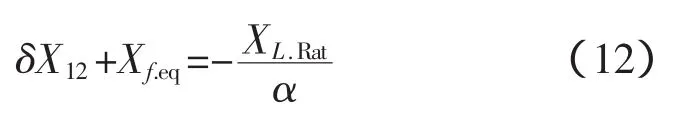
将式(10)带入可得
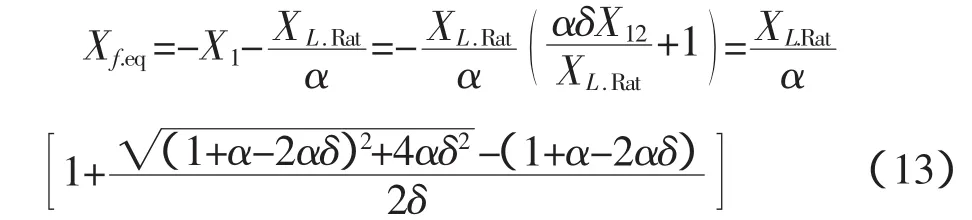
另一方面,滤波器工频电压下等效电抗Xf.eq由各高次谐波滤波器确定

在只有5次、7次谐波滤波器的情况下(第三绕组三相接成三角形连接关系)按照式(14)得
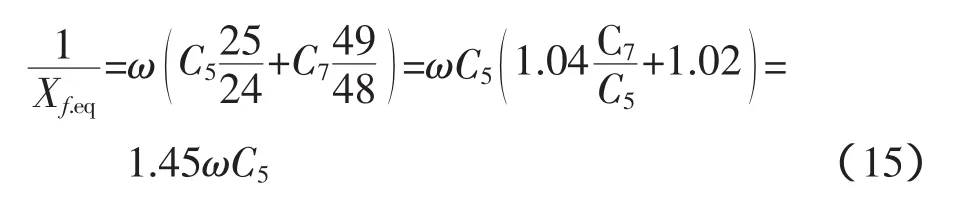
由此可得
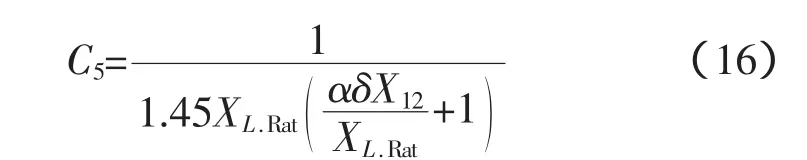
式中,C7=0.4C5[10]。应该注意的是,这里C5C7的是归算到一次绕组侧的参数。在晶闸管触发角为180°的情况下,通过滤波器的电流(归算到一次侧)为
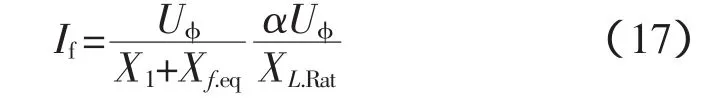
滤波器电容上的电压(归算到一次侧)为

由此可见,电容电压略高于由变压器变比所决定的额定电压。则电容无功功率为
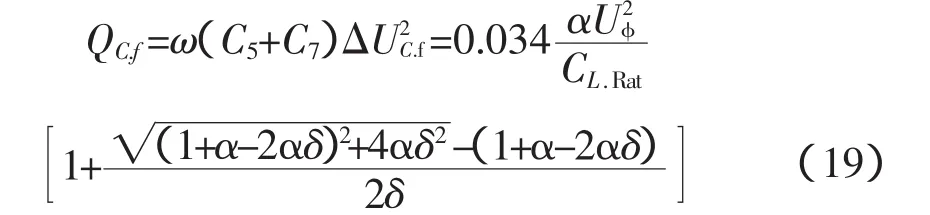

很明显此比值大于1,这说明电容器的一部分功率补偿了滤波器中电感的功率,并且这个比值随着和值的增大而增大,如图2所示。

图2 滤波电容总功率相对于控制补偿器总额定容性功率的比值QC.f/QC.csttr随相对电抗值在不同情况下的曲线变化关系(1-α=0.2;2-α=0.4;3-α=0.6;4-α=0.8;5-α=1.0)Fig.2 Ratio QC.f/QC.csttr between total power of filter capacitors and total capacitive power of controlled com pensator changing w ith relative reactance(1-α=0.2;2-α=0.4;3-α=0.6;4-α=0.8;5-α=1.0)
出于经济性的考虑,δ值最好在小于或等于0.6范围内,如图2所示,尽可能使第三绕组位置远离第二绕组。
由图1可以看出,当晶闸管触发角为180°时,第二分支路电流为0,如果二次三次绕组匝数相等,此时晶闸管模块上所承受的额定电压为三次绕组的电压,也就是说二次绕组的额定电压可以由以下关系决定

式中,ΔUC.f由(18)决定;Kt2-3为2次相对于3次绕组之变比。由图1可得二次绕组额定电流和一次绕组电压之间的关系
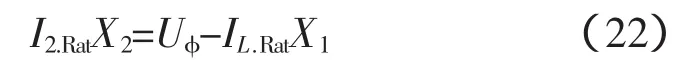
或者

由此可得二次额定电流

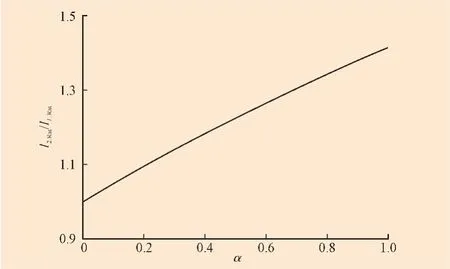
图3 CSRT二次额定电流随α(容性补偿功率相对感性补偿功率)变化曲线Fig.3 Curve of rated secondary current of CSRT changing w ith α
由此可以通过式(24)来确定晶闸管模块的额定电流IT.Rat,并且可以得到必需的变比

由此可见,控制补偿器的一二次变比要比控制电抗器小(在相同功率,相同δ和α)。这样,通过提高滤波器电容的容量实现了控制补偿器在容性工作状态下对容性电流的调整(可达到100%IL.Ra)t。通过在二次侧控制晶闸管的触发角在180° ~90°变化,可以使得控制补偿器所提供的电流从额定容性电流变化到额定感性电流(IC.Rat—IL.Ra)t。
3 晶闸管触发角与补偿系数之间的关系
由上节电流变化范围可知,当晶闸管触发角在某一个角度时,必然使得容性电流和感性电流大小相等,相互抵消,这时控制补偿器不提供任何电流给系统。感性电流和容性电流在内部相互补偿(此时一次绕组中电流为0)。
由图1(b)可以看出,当系统绕组侧电流过零点时,第2支路和第3支路的等效电抗大小相等,由式(11)可得

此时因为1支路电流为零,所以整个电压被2、3支路所承担,此刻流过2次绕组的电流为
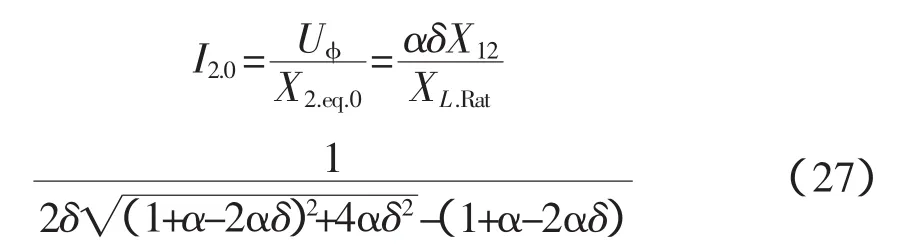
这个电流和二次额定电流的比值为

此关系表明,在此时刻二次绕组电流相对值仅与2个参数有关,然而实际计算表明这个关系只依赖于参数α,其曲线变化(如图4曲线1)近似(误差不超过2%)于
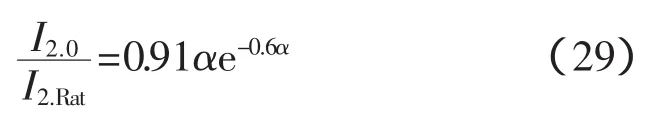
这个比值可以用来确定晶闸管触发角(当CSRT的一次侧电流过零点时),因为通过晶闸管的电流相对值和触发角之间的关系是确定的(如图6所示),但是这个关系的前提条件是电压恒定,所以应该对式(29)进行校正,在额定感性补偿工作方式下X2=(1-δ)X12值是不变的,二次侧电压随着二次侧电流的增大而升高


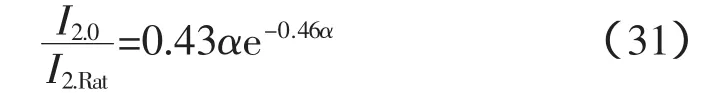

图4 当系统绕组中电流过零点时,二次绕组电流相对值随参数的变化关系(1为没有经过校正过的曲线,2为经电压校正过的曲线)Fig.4 When current of system winding is zero,curve of relative current of secondary w inding changing with parameters(1-without voltage correction,2-with voltage correction)

图5 二次电压相对值在晶闸管完全导通的情况下随参数α的变化关系Fig.5 Relative secondary voltage(in case of transistor fully conductive)changing w ith α
图4中曲线2和图6可以确定当一次侧电流过零点时,晶闸管触发角、导通角和α之间的关系,如表1所示。
看得出随着α值的增大,晶闸管的触发角在减小,得到这些数据可以进一步来确定CSRT的触发角和一次电流相对值之间的关系。由于在一次电流过零时,二次侧感性电抗绝对值等于3次绕组容性电抗绝对值,将式(5)两边都乘一个因子K可得:
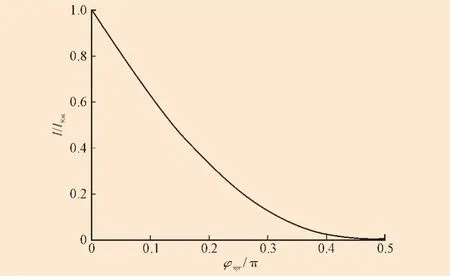
图6 通过晶闸管的电流与触发角之间的关系Fig.6 Relationship between current flow ing through transistor and firing angle

表1 晶闸管触发角和导通角之间的关系Tab.1 Relationship between the firing angle and conductive angle of transistor

这样CSRT的等效电抗为
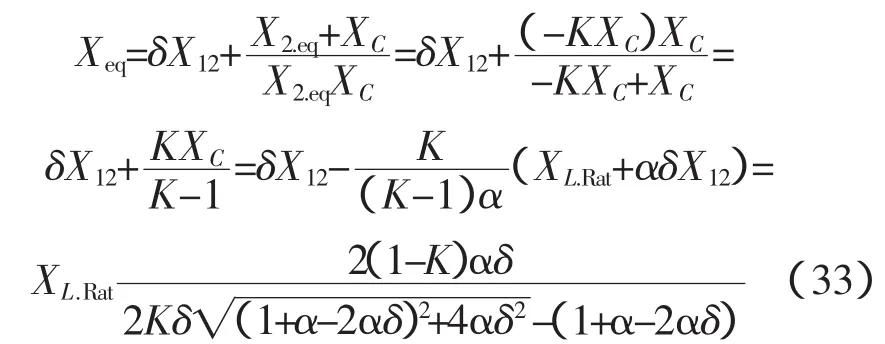
由此,CSRT的电流相对值在K取任意值的情况为
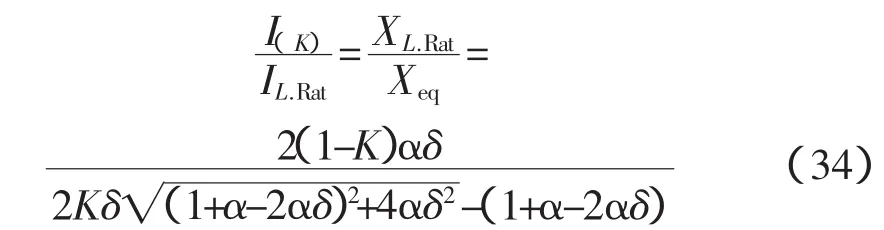
由于参数δ变化范围很小而且对上述关系的影响不大,所以我们固定δ=0.5。这样式(34)简化为
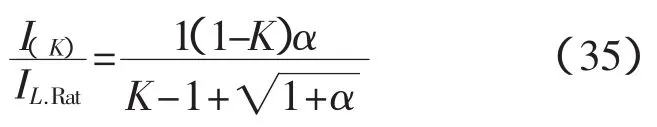
下面是确定CSRT的电流相对值和晶闸管触发角之间关系的过程。首先按照图4中的曲线2确定了当一次电流过零时,晶闸管电流的相对值。比如当α=1时,按照上述方法可得φspr=129°和二次电流相对值I2/I2.Rat=0.3,如果晶闸管支路的等效电抗减少2倍(K=0.5),那么经过晶闸管的相对电流将会变成I2/I2.Rat=0.3/0.5=0.6。按照图6可以得出晶闸管触发角为110°。这样我们可以确定所有一次绕组电流和晶闸管触发角之间的关系(一次电流由IL.Rat变化到IC.Ra,见图7)。可以看出在同一电流下触发角随着α值的减小而增大。

图7 CSRT的电流相对值和晶闸管触发角之间的关系曲线Fig.7 Curve of relationship between relative current of CSRT and firing angle of transistor
4 实验分析
在印度BHEL公司(г.Бхопал)所属的变压器厂进行了在CSRT基础上实现容性补偿的试验,试验一次侧额定电压11 kV,容量为2 MV·A,δ=0.67,3个并联在补偿绕组中的电容分别为720 μF、360 μF、180 μF,这次试验完全肯定了上述分析的正确性。当控制绕组断开时,在额定电压下,CSRT提供容性电流为105 A、40 A和17A(α=1,0.38,0.16)。当控制绕组短路时,CSRT提供感性电流为96 A、99 A和104 A(额定电流为105 A)。此项实验验证了上述理论实现的可能性,也为CSRT的广泛应用提供了实践依据。
5 结论
提出了一种双向无功控制补偿器,通过提高其副边补偿绕组中高次谐波滤波器电容的大小,实现不仅能吸收无功,而且可发出无功的双向补偿功能,从而在高压输电线路输送功率变化时,通过快速调整装设在控制绕组中的单个晶闸管模块的导通角,即可实现无功功率的静态输出或吸收的2种工作方式的控制,实现长距离高压输电线路无功的柔性补偿。这种变压器式静态无功控制功率补偿器的优势是:
1)一次侧绕组可以不需要经过断路器而直接接入高压线路。
2)只需要提高一定的电容容量即可实现较宽的无功功率范围(从吸收额定感性无功功率到发出额定容性无功功率)。
3)晶闸管模块安置在二次绕组中,降低了对晶闸管模块的绝缘特性要求,降低了成本。
[1] 陈伯超,田翠华,梁柏华,等.单相可控电抗器的一种谐波抑制原理及实现[J].中国电机工程学报,2002,22(3):63-67.CHEN Bo-chao,TIAN Cui-hua,LIANG Bai-hua,etal.Principle and implementation of a harmonic depression approach for single-phase controlled saturable reactor[J].Proceedings of the CSEE,2002,22(3):63-67(in Chinese).
[2] 牟宪民,魏晓霞,纪延超,等.串联型可控饱和电抗器谐波特性分析[J].电力自动化设备,2007,27(3):14-17.MU Xian-min,WEI Xiao-xia,JI Yan-chao,etal.Harmonic characteristic analysis of serial controllable saturated reactor[J].Electric Power Automation Equipment,2007,27(3):14-17(in Chinese).
[3] Александров Г Н . Управляемый шунтирующий реактор трансформаторного типа[J].Электротехника,1996,67(10):54-61.
[4] 李达义,陈乔夫,贾正春.基于磁通可控的可调电抗器的新原理[J].中国电机工程学报,2003,23(2):116120.LIDa-yi,CHENQiao-fu,JIAZheng-chun.Novelcontrollable reactor based on controllable flux[J].Proceedings of the CSEE,2003,23(2):116-120(in Chinese).
[5] REICHERT K,KAUFERLE J,GLAVITSCH H.Controllable reactor compensator for more extensive utilization of high voltage transmission systems[C].International Conference on Large High Voltage Electrical Systems,1974(12):31-34.
[6] ALEXANDROW G N,TRIPATHY A K.Controlled shunt reactor for 400 kV network[C].CIGRE,2002,37/38/14-1.
[7] Александров Г Н.Подавление высших гармонических в управляемых шунтирующих реакторах трансфо -рматорного типа.Изв[J].РАН.Энергетика,1999(3):18-25.
[8] 田铭兴,励庆孚.变压器式可控电抗器的谐波分析和功率级数计算[J].中国电机工程学报,2003,23(8):168-171.TIAN Ming-xing,LI Qing-fu.Harmonic current and power-step number of controllable shunting reactors of transformer type[J].Proceedings of the CSEE,2003,23(8):168-171(in Chinese).
[9] 田铭兴,励庆孚.变压器式可控电抗器的限流电抗计算和仿真[J].西安交通大学学报,2004,38(8):820-824.TIAN Ming-xing,LI Qing-fu.Calculation and simulation of a controllable reactor of transformer type[J].Journal of Xi’an Jiaotong University,2004,38(8):820-824 (in Chinese).
[10] Александров ГН,Лунин ВП.Управляемые реакторы[M].-Санкт- Петербург. Второе издание Центра подготовки кадров СЗФ АО《ГВЦ Энергетики》,2005.
[11] 刘言菊,田铭兴,何利,等.单相磁阀式可控电抗器的设计原理研究[J].电网与清洁能源,2011,27(7):36-38.LIU Yan-ju,TIAN Ming-xing,HE Li,et al.Design principle of single-phase magnetic valve controlled reactor[J].Power Systemand Clean Energy,2011,27(7):36-38(in Chinese).
[12] 刘红恩,李和明,雷晰,等.基于PSCAD的分级式可控并联电抗器仿真研究[J].电力科学与工程,2012,28(1):13-17.LIU Hong-en,LI He-ming,LIE Xi,et al.Simulation research on the stepped controlled shunt reactor based on PSCAD[J].Electric Power Science and Engineering,2012,28(1):13-17(in Chinese).
[13] 蒋长洪,李兴建,曹五顺.新型磁控式可控电抗器在电网电容电流自动补偿中的应用[J].电力科学与工程,2003(1):23-25.JIANGChang-hong,LIXing-jian,CAOWu-shun.Application of magnetism-controlled reactors to capacitive current automatic compensation in networks[J].Electric Power Science and Engineering,2003(1):23-25(in Chinese).
[14] 王长善,张卫星,范文涛.磁阀式可控电抗器的控制回路及其控制特性[J].电力科学与工程,2005(1):46-49.WANG Chang-shan,ZHANG Wei-xing,FAN Wen-tao.Controlling loop of controllable magnetic-valve reactors and its characters[J].Electric Power Science and Engineering,2005(1):46-49(in Chinese).
[15] 张名捷,程汉湘,范隽宏.裂心式磁控电抗器的偏磁特性分析[J].南方电网技术,2012,6(3):94-99.ZHANG Ming-jie,CHENG Han-xiang,ZHANG Jian-hong.Analysis on DC magnetic bias of crack core type magnetic controlled reactor[J].Southern Power System Technology,2012,6(3):94-99(in Chinese).
[16] 李维亚.线路变压电抗器作为500 kV及特高压线路并联电抗器的解决方案[J].南方电网技术,2010,4(1):67-70.LI Wei-ya.The shunt transformer-controllable reactor as a solution for 500 kV and UHV Transmission Line Shunt Reactor[J].Southern Power System Technology,2010,4(1):67-70(in Chinese).
