洛伦兹曲线的半参数估计

俞翰君

（北京大学 数学科学学院，北京 100871）

洛伦兹曲线的半参数估计

俞翰君

（北京大学 数学科学学院，北京 100871）

洛伦兹曲线与基尼系数是研究社会收入分配差异的重要工具。社会收入分配是一个复杂的过程，用尽可能精确的曲线给出洛伦兹曲线的估计进而给出基尼系数的估计，历来是统计学者和经济学者的工作目标。基于将参数方法与非参数方法相结合的思想给出洛伦兹曲线的半参数估计，进而导出基尼系数的估计，并据此进行了实证分析。

收入分布函数；洛伦兹曲线；基尼系数；Beta分布；Pareto分布；半参数估计

一、引 言

奥地利统计学家洛伦兹1907年在研究社会财富分配状况时提出了著名的洛伦兹曲线，即在一个总体（国家、地区）内以“最贫穷的人口计算起一直到最富有人口”的人口百分比对应其收入百分比的点组成的曲线，如图1中的曲线OL。通过洛伦兹曲线，可以直观地看到一个国家或地区收入分配平等或不平等的状况。

意大利经济学家基尼1912年根据洛伦兹曲线提出了定量测定收入分配差异程度的指标——基尼系数。基尼系数是比例数值，取值在0和1之间，即图1中A的面积与A＋B面积之比，是国际上用来综合考察居民收入分配差异状况的一个重要分析指标。

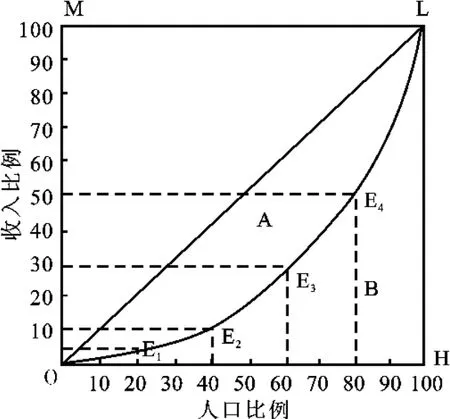
图1 洛伦兹曲线图

为了获得基尼系数需要用到洛伦兹曲线，而为了获得洛伦兹曲线需知道收入分布函数。收入分布函数是某地区的全体居民中，个人收入不超过某值的居民所占的比例［1］。在统计上估计收入分布函数的方法主要有两种：参数方法和非参数方法。参数方法假定收入分布函数类型已知，利用样本数据对分布中的未知参数给出估计从而拟合分布函数曲线。19世纪末，意大利经济学家帕累托提出了拟合收入分布的模型——Pareto分布。该分布得到了广泛应用。此外，对数正态分布、Gamma分布、Beta分布和Weibull分布等也曾用来刻画收入分布函数，这些收入分布函数各有千秋：James B．McDonald等人在研究中发现Pareto分布估计高收入阶层较精确；Beta分布、对数正态分布和Gamma分布对中等收入阶层估计较为精确［2－3］；另一种方法是非参数方法，非参数方法主要是利用经验分布函数、核密度函数以及样条等方法直接对收入分布函数进行估计。胡祖光等利用核密度函数给出了中国城乡居民收入分布的动态演进［4］91－111；黄恒君等给出了基于B样条的收入分布函数形式［5］。

2007年Cowell等给出了洛伦兹曲线的半参数估计，其主要思想是考虑到收入分布的上尾受污染的可能性较大，对收入选取一个适当的门限值x0，x0以下的收入用经验分布函数估计，x0以上的收入用Pareto分布估计［6］，并将该方法应用于英国1981年的7 470个家庭的可支配收入数据中。

通过比较发现，参数方法和非参数方法估计收入分布函数各有优缺点：参数方法估计的模型形式单一，统计上较为容易处理，但社会收入分配是一个复杂的过程，一般而言不可能完全用一条较为理想的曲线来描述，因此拟合效果往往不够理想；非参数方法由于本质上是利用频率来估计概率，因而理论上比较理想，但是该方法在统计上处理较为复杂，特别是当数据受到污染时（如记录错误或受访者不愿意回答等，主要出现在特别高和特别低的收入数据中）可能会导致结果不准确；半参数方法综合了参数方法和非参数方法各自的优点，克服了它们各自的缺陷，通过对实际问题的缜密研究，灵活地界定了参数方法和非参数方法的应用范围，拟合数据时可以更好地与实际吻合，并可以根据实际情况调整参数估计和非参数估计的范围。

Cowell等在研究收入分布时仅对高收入数据运用参数方法。本文拟选择两个门限值x1和x2（x1＜x2），对x1和x2中间部分用经验分布函数估计，两点之外用分布函数估计，大于x2的部分用拟合效果比较好的Pareto分布，小于x1的部分尝试用Beta分布，由此可导出洛伦兹曲线，进而得到基尼系数。

洛伦兹曲线的半参数估计方法克服了参数方法和非参数方法的缺陷，其优点如下：一是充分利用了参数方法和非参数方法的优点，能够使拟合的结果更加符合实际情况；二是可以根据实际情况调整参数估计和非参数估计的运用范围，有利于一个地区在不同时期或不同地区在同一时期的洛伦兹曲线的比较。

二、洛伦兹曲线的半参数估计方法

（一）收入分布函数的半参数表达

由于计算基尼系数所用的数据是家庭平均收入，本文中收入分布函数的定义为某地区的全体家庭中，家庭平均收入不超过某值的家庭所占的比例。假设某地区的家庭平均收入为随机变量X，令为所有单变量收入分布函数的集合，其支撑为，x0＝inf为X的最低值。X服从的分布函数F∈，则家庭平均收入不超过x的家庭所占的比例为F（x）＝P（X≤x）。

F可以为不含参数的经验分布函数Fn，也可以为含参数的分布函数Fθ。常见的含参数的收入分布函数有Beta分布、Dagum分布、Gamma分布、Lognormal分布、Pareto 分布、Singh-Maddala分布、Weibull分布等。

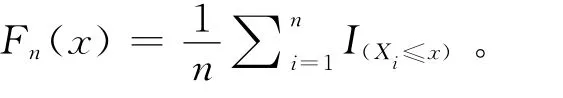
由于Pareto分布拟合高收入数据较为理想，因此大于x2的部分采用Pareto分布进行拟合，其密度函数为：

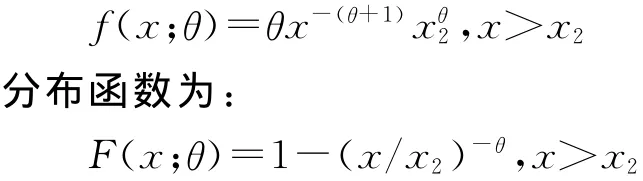
未知参数为θ。

由于Beta分布的支撑有界，且拟合中低收入数据较为理想，故位于x0与x1之间的部分采用Beta分布进行拟合，其密度函数为：

（二）洛伦兹曲线的半参数表达

对于给定的收入分布函数F，C（F；u）关于u的图像为广义洛伦兹曲线。L（F；u）关于u的图像为相对洛伦兹曲线。本文的研究对象为相对洛伦兹曲线，以下简称为洛伦兹曲线。

为得到洛伦兹曲线的半参数表达，首先要求出收入分布函数F（x）对应的Q（F；u）。因x1和x2为两个不同的门限值，则存在α1＝Fn（x1）和α2＝Fn（x2），满足x1＝Q（Fn；α1）和x2＝Q（Fn；α2），故式（1）也可化为：

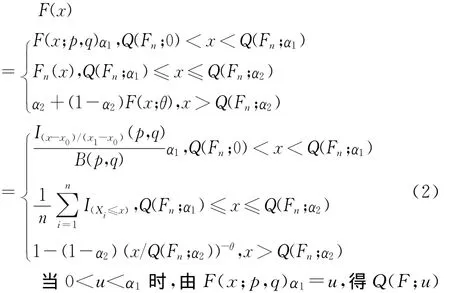
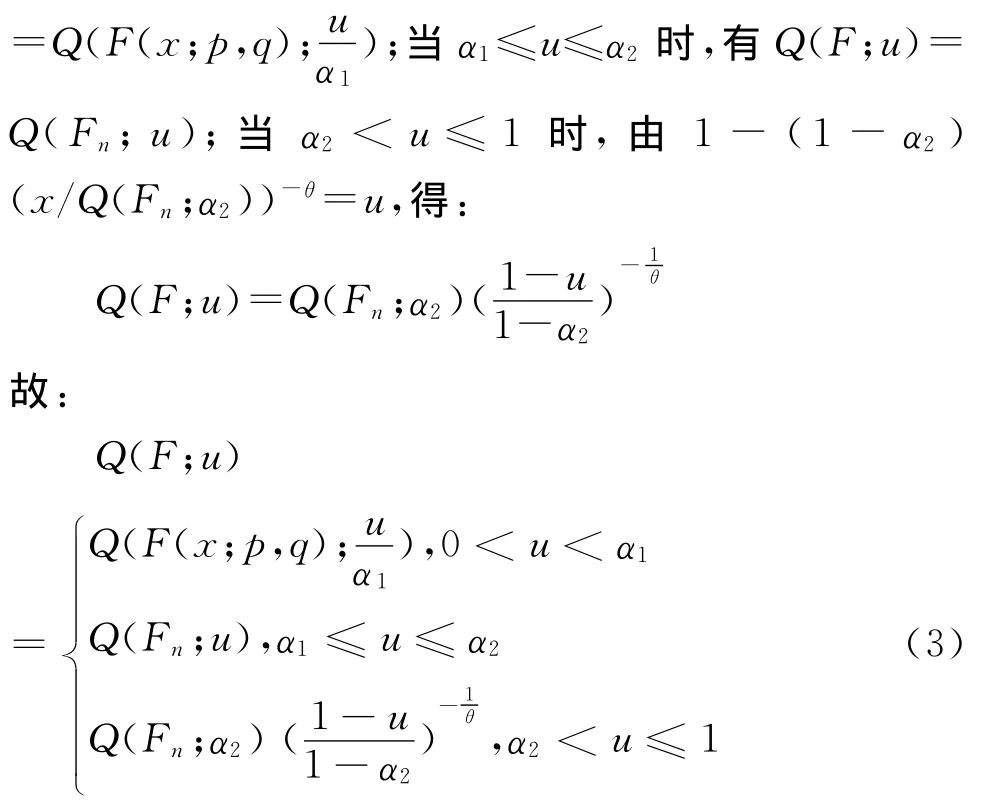
为简便起见，记F1（x）＝F（x；p，q）α1，F2（x）＝α2＋（1－α2）F（x；θ），则100u%最底层家庭的平均收入C（F；u）为：

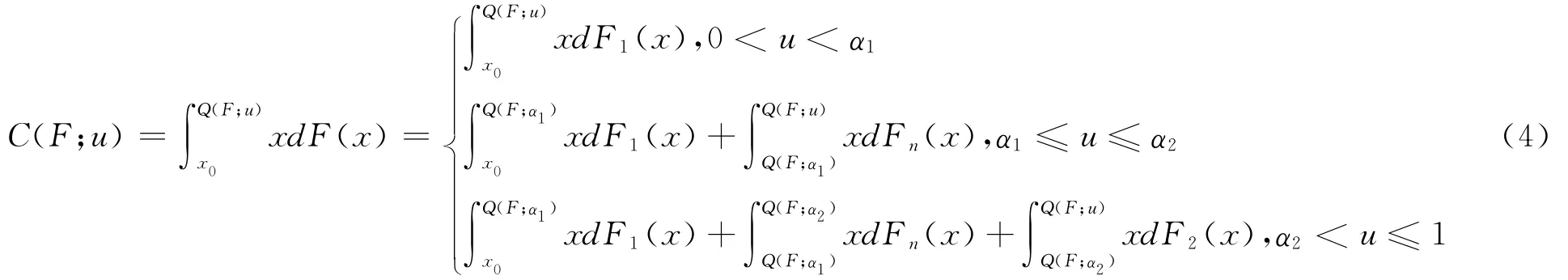
通过分段计算C（F；u），得到：

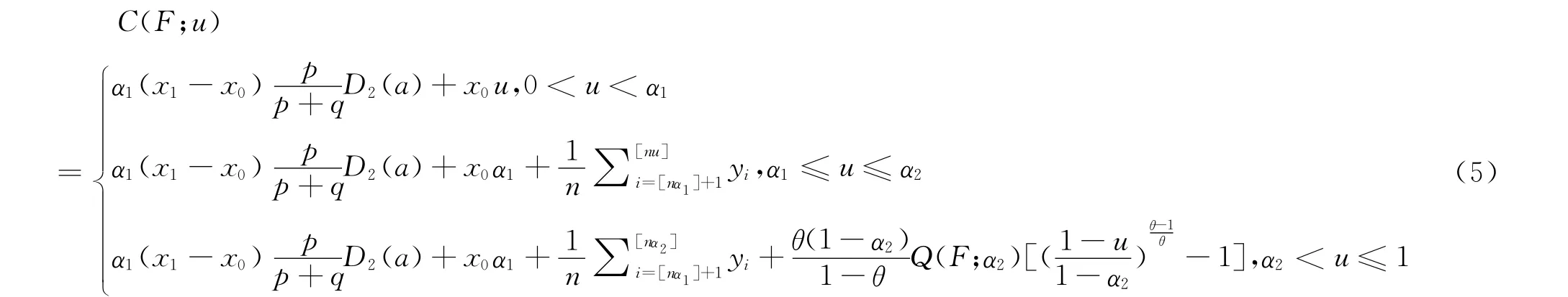
（三）Pareto分布的参数估计

收入分布函数的高收入部分利用Pareto分布进行拟合，需要对未知参数θ进行估计。Pareto分布的密度函数形式简单，考虑采用极大似然方法估计θ。若k个最高的收入样本yn－k＋1，yn－k＋2，…，yn服从Pareto分布，求得θ的极大似然估计为：

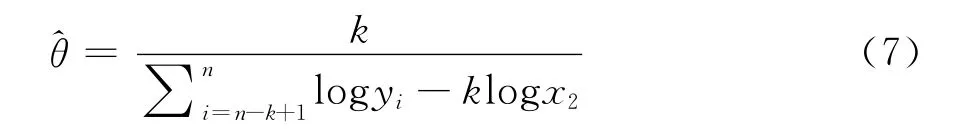
（四）Beta分布的参数估计

收入分布函数的低收入部分利用Beta分布进行拟合，需要对未知参数p和q进行估计。由于Beta分布的密度函数含有beta函数，求解极大似然估计较为困难，故采用矩估计的方法估计未知参数。若m个最低的收入样本y1，y2，…，ym服从Beta分布，求得p和q的矩估计表达式为：

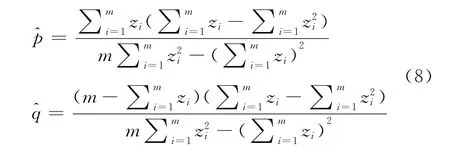
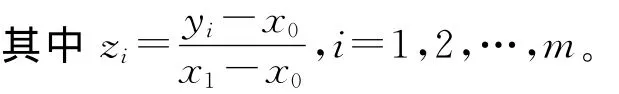
（五）门限值的选取

对门限值x1和x2（x1＜x2）的选取是估计收入分布函数，进而得到洛伦兹曲线的关键。首先考虑x2的选取方法。验证数据是否服从Pareto分布的比较常用的方法是利用Pareto分布的Q－Q图［7］573－579。重新整理Pareto分布的分布函数，有：

其次考虑x1的选取方法。对x1的选取采用如下准则：

1．依次取前m 个收入样本y1，y2，…，ym，m＝m0，…，n－k（m为一个变化的数，每取完一组收入样本后其值增加1，再取下一组，其中m0要大于一定的值以防止参数估计时出现过度拟合，k为已确定的服从Pareto分布的样本个数），分别利用给定的参数估计方法计算参数值＾pm和＾qm。

6．在通过KS检验的m中选择使得Gm达到最小的m，则对应的临界值为x1＝ym，即yi，i＝1，2，…，m服从Beta分布。

（六）基尼系数的计算方法

由于上述洛伦兹曲线L（F；u）形式较为复杂，用积分方法计算基尼系数不易，故本文采用“离散模拟法”计算基尼系数，方法如下：

1．根据式（6），得到μ（F）。

三、实证分析

（一）数据来源

利用“中国营养和健康调查”（China Nutrition and Health Survey，以下简称 CHNS）2009年的城镇家庭人均年收入数据进行数据分析［8］。该调查由美国北卡罗莱纳大学教堂山校区的罗莱纳州人口中心和中国疾病控制和预防中心的国家营养和食品安全所联合执行。调查依据地理位置、经济发展程度、公共资源的丰富程度和健康指数，对中国东、中和西部8个省份（分别为辽宁、江苏、山东、河南、湖北、湖南、广西和贵州）随机抽取家庭户作为样本。这些省份无论在地理位置还是经济发展水平上都具有多样性，因此可以作为一个比较有代表性的样本来研究当代中国［5］。

下文将对CHNS2009年城镇家庭人均年收入的1 401个数据（数据经过CPI平减，且去掉了非正的收入数据）进行分析，将分别给出参数估计值、拟合的收入分布函数、拟合的洛伦兹曲线和基尼系数估计值。

（二）数据描述

该数据的描述性统计量如表1所示。

表1 数据描述统计量表

（三）收入分布函数的拟合

1．Pareto分布参数估计与门限值。由第二部分知，可以先通过式（10）确定哪些数据服从Pareto分布，再进行参数估计。绘制Pareto分布Q－Q图，得到图2。

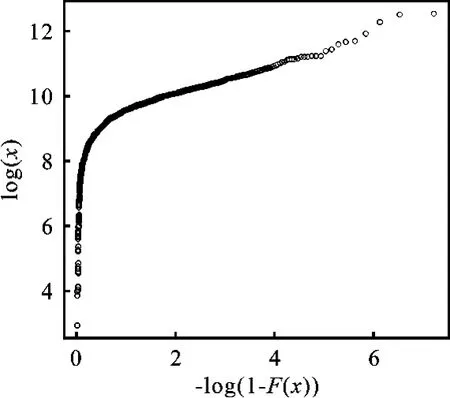
图2 Pareto分布Q－Q图

由图2知，图像弯曲而非直线，说明数据整体不服从Pareto分布。由于Pareto分布拟合高收入数据较为准确，为了使图像清晰，选取年人均收入最高的40个数据绘制图像，得到图3。

从图3可以看出，最高的10个收入样本近似位于一条直线上，可认为该10个数据服从Pareto分布，故门限值为x2＝77 932．52，α2＝Fn（x2）＝0．993 6。

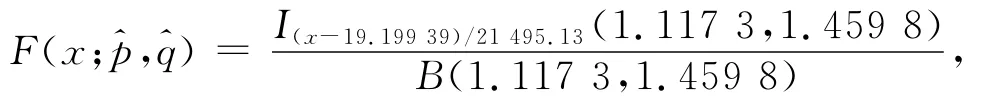
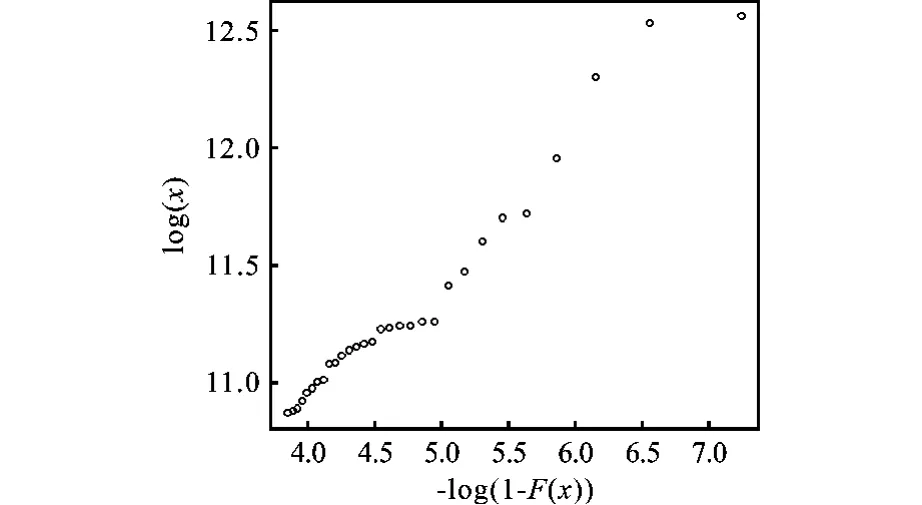
图3 40个高收入数据的Pareto分布Q－Q图

3．收入分布函数表达式与图像。由式（2）并结合参数估计值与门限值，得到该组数据的收入分布函数半参数表达式为：

2．Beta分布参数估计与门限值。为确定Beta分布的参数与门限值，需按照上文给出的方法，依次计算前m（m＝m0，…，1 391，这里取m0＝10）个收入数据估计的参数并比较估计的优劣，从中选出最好的估计。通过循环计算，最终得到门限值为x1＝21 514．33，α1＝Fn（x1）＝0．811 6，参数＝1．117 3和＝1．459 8，则 Beta 分 布 的分 布 函 数 为：

绘制收入分布函数图像，得到图4。

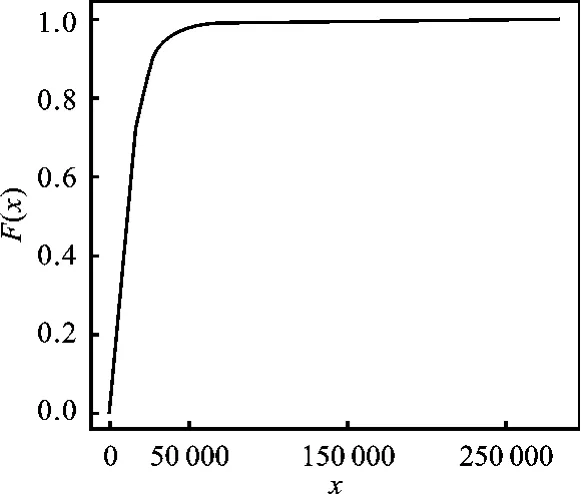
图4 收入分布函数拟合图像

（三）洛伦兹曲线的拟合

利用拟合的收入分布函数及式（5）和（6），绘制出如图5所示的洛伦兹曲线。

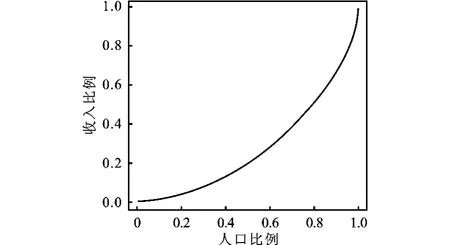
图5 洛伦兹曲线拟合图像

（四）基尼系数的估计

利用第二部分的方法，得到基尼系数的估计值＾G＝0．455 7，即2009年中国城镇基尼系数的估计值为0．455 7。

四、结 论

考虑到参数方法和非参数方法在估计洛伦兹曲线中各有利弊，本文先对收入分布函数进行半参数估计，进而给出洛伦兹曲线的半参数表达。

首先，根据拟合优度准则和Q－Q图选择了收入的两个门限值x1和x2（x1＜x2），对x1以下的部分用Beta分布估计，x2以上的部分用Pareto分布估计，分布的选取依据为以往的文献研究；对x1和x2之间的部分用经验分布函数估计，经验分布函数能够起到较好的连接作用。选定分布函数之后，利用极大似然估计和矩估计对未知参数进行估计，进而得到了收入分布函数的半参数表达。根据洛伦兹曲线的定义，由已知的收入分布函数表达式推导得出洛伦兹曲线的半参数表达，并给出了基尼系数的估计方法。

其次，将所给方法应用于CHNS 2009年城镇居民家庭年人均收入数据中，给出了收入分布函数和洛伦兹曲线的图像，并通过计算得到了基尼系数的估计值为0．455 7。该结果表明，中国2009年城镇居民家庭人均年收入差距较大，贫富分化较显著。

本文的优点在于，不采用单一的分布函数估计收入分布函数和洛伦兹曲线，而是根据分布函数各自的特点确定其适用范围，使估计的效果更准确。本文的不足之处在于，收入分布函数的非参数部分利用的是经验分布函数，虽然直观并且形式简单，但不光滑，估计效果可能不够理想。

［1］ 祁丹丹，王青．加入WTO以来我国农民收入变动趋势分析及收入预测［J］．西北农林科技大学学报；社会科学版，2011，11（2）．

［2］ McDonald James B．Some Generalized Functions for the Size Distributionof Income［J］．Econometrica，1984，52（3）．

［3］ Singh S K，Maddala G S．A Function for Size Distribution of Incomes［J］．Econometrica，1976，44（5）．

［4］ 胡祖光．基尼系数与收入分布研究［M］．杭州：浙江工商大学出版社，2010．

［5］ 黄恒君，刘黎明．一种收入分布函数序列的拟合方法及扩展应用［J］．统计与信息论坛，2011，26（12）．

［6］ Cowell Frank A，Victoria-Feser Maria-Pia．Modelling Lorenz Curves：Robust and Semi-parametric Issues［C］．New York：Springer Science＋Business Media，2008．

［7］ Norman L，Kotz J S，Balakrishnan N．Continuous Univariate Distributions［M］．2nd ed．New York：Wiley，1995．

［8］ CHNS 2009年数据［DB／OL］．（2011－01－01）［2012－03－18］．https：／／www．cpc．unc．edu／projects／china．

The Semi Parametric Estimation of Lorenz Curves

YU Han-jun
（School of Mathematical Sciences，Peking University，Beijing 100871，China）

Lorenz curves and Gini index are important in dealing with the gap of social income distribution．The allocation of social income is a very complicated process，and it is for decades the goal of statisticians and economists to estimate the Lorenz curves as accurate as possible．This paper is based on the thought of combining parametric approach with nonparametric approach to give the semi parametric approach of Lorenz curves and furthermore the estimation of Gini index．An example with true data is analyzed by the whole approach．

income distribution；Lorenz curves；Gini index；Beta distribution；Pareto distribution；semi parametric estimation

F224．0

A

1007－3116（2013）05－0019－06

2012－11－16

俞翰君，女，山东济南人，博士生，研究方向：生物医学统计，可靠性分析。

（责任编辑：崔国平）