基于XDLVO理论的黏性泥沙絮凝模拟格子玻耳兹曼模型

乔光全，张庆河，张金凤，程洪剑，卢 昭

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 中交水运规划设计院有限公司，北京 100007)

黏性泥沙在我国海岸河口地区分布广泛，其絮凝沉降过程与港口和航道淤积、海岸河口环境变化等密切相关，对黏性泥沙絮凝沉降特性的研究具有十分重要的意义．海岸河口地区影响黏性泥沙絮凝沉降的因素既有泥沙颗粒矿物质组成、泥沙浓度等黏性泥沙自身特性，又有海水盐度和河口淡水属性等水体环境特性．因此，描述黏性泥沙絮凝沉降时，需要尽可能包括上述各种因素的影响．

近年来，一些学者开始利用数值模拟方法研究黏性泥沙絮凝沉降，如洪国军等[1]用受限的絮团聚集模型(diffusion limited cluster aggregation，DLCA)研究了黏性细颗粒泥沙的絮凝沉降过程，得到了分形维数和颗粒浓度的关系，讨论了絮凝-沉降过程的各种特性．王龙等[2]将 XDLVO 理论(extended Derjaguin-Landau-Verwey-Overbeek theory)和无参数可解性的加速斯托克斯动力学(accelerated Stokesian dynamics)方法结合，对黏性泥沙絮凝沉降进行了数值研究，获得了盐度、浓度和水合作用参数对泥沙沉降絮凝的影响．上述数值模型虽然能够获得有关黏性泥沙絮凝变化的规律，但不能完整描述颗粒絮凝的水动力过程，因而难以全面考虑各种因素，如水流紊动等对絮凝的影响．

格子玻耳兹曼(lattice Boltzmann，LB)方法是一种近年来得到快速发展的流动模拟方法，具有编程简单、易于并行求解颗粒与流体全尺度相互作用问题等优点．在合理考虑颗粒之间相互作用力和定义颗粒絮凝状态的情况下，LB方法可以从微观水动力角度完整描述絮凝过程，为深入研究黏性泥沙絮凝规律提供了工具．张金凤等[3-4]采用LB方法，考虑颗粒之间的范德华吸引力，建立了黏性泥沙不等速沉降絮凝的数值模型．卢昭[5]和程洪剑[6]在该模型中引入了DLVO(Derjaguin-Landau-Verwey-Overbeek)理论，考虑了颗粒间范德华力和双电层作用力，模拟了盐度和浓度对絮凝的影响．上述工作逐步合理地考虑了颗粒间相互作用力，但由于模型中没有反映泥沙矿物种类的参数，因此尚未能对矿物种类等因素对黏性泥沙絮凝的影响进行深入分析．

为了在 LB模型中更全面地反映各种因素对黏性泥沙絮凝沉降的影响，笔者将颗粒之间相互作用的XDLVO理论引入 LB模型，并利用模型分别对伊利土、蒙脱土和高岭土3种黏土矿物泥沙颗粒间的絮凝进行模拟，以分析矿物质成分对絮凝的影响．

1 黏性泥沙絮凝的LB模型

1.1 LB模型简介

LB方法采用微观流体的粒子速度分布函数描述流体运动，fi的演化方程为

式中：fi为在离散时间t内、格子r处速度为 ci的假想流体粒子数；i为速度方向；Δi为线性碰撞算子，表示为

LB模型可模拟颗粒和流体的相互作用．Ladd[7]提出了处理颗粒运动的LB算法：流体格点位于颗粒的外部，每个格点的速度为bc，bt+Δrc位于颗粒的内部，格子的中点表示固体颗粒边界，格点的连线穿过流-固边界表面，流体粒子沿着格子连线运动并与悬浮固体颗粒发生碰撞和相互作用，在流体和固体间的局部能量交换过程中保持能量守恒．流体粒子每个时间步离开原来格点沿规定方向运动到邻近格点，当流体粒子运动到固定壁面时，利用全反射条件可满足壁面无滑移．因此，流体-固体颗粒边界的离散模型为

颗粒的平动速度和转动角速度可根据平动加速度α和转动角加速度 β表达式逐步积分获得，其表达式分别为

式中：m和 J分别为泥沙颗粒或絮团的质量和动量矩；F和M分别为泥沙颗粒或絮团受到的总外力和总力矩．对于黏性细颗粒泥沙，颗粒受到的总力可表示为

1.2 颗粒间相互作用力

20世纪80年代以来，Somasundaran[9]和van Oss等[10]在研究黏土矿和磁铁矿的凝聚行为时发现，极性溶液中距离很近的 2个颗粒表面由于氢离子的黏结作用会形成路易斯酸碱能(acid-base energy)，且在短距离情况下，这种 A-B相互作用能较静电排斥能和范德华吸引能大 1～2个量级．将这种作用加入到DLVO理论中，形成了 XDLVO理论．胡岳华等[11]也认识到这种力的存在，给出了颗粒间相互作用能的计算公式，并通过物理实验验证了XDLVO理论的适用性．Wu等[12]用XDLVO理论和DLVO理论分别对各种矿物颗粒悬浮液的稳定性进行了研究，发现前者比后者得到的结果更为精确．

由于 XDLVO理论考虑了颗粒之间的范德华吸引力、静电排斥力和A-B作用力，更为合理地描述了细颗粒及胶体在电解质溶液中的凝聚行为，因此这里采用 XDLVO理论描述黏性泥沙颗粒间的相互作用．XDLVO理论将颗粒之间的总势能表示为

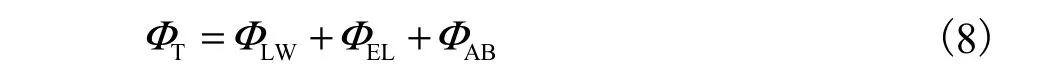
1.2.2 双电层作用力

式中：e为元电荷，e＝1.6×10-19,C；NA为阿伏伽德罗常数，NA＝6.022×1023/mol；k为 Boltzmann 常数，k＝1.38×10-23,J/K；T为绝对温度，K；cm为阳离子浓度，mol/L；zm表示阳离子化合价，无量纲．

双电层作用力为双电层作用能对距离的负导数，即

1.2.3 A-B作用力

A-B作用能是XDLVO理论区别于DLVO理论的重要作用能，其表达式[14]为

式中：λAB为衰减长度，与颗粒本身的特性有关，具有

1.3 LB模型中XDLVO势能合理性分析

A-B力中较为敏感的参数为衰减长度ABλ[3]，为了验证模型的合理性，这里模拟不同衰减长度条件下，2个不等直径的球形泥沙颗粒在静水中的沉降过程．计算范围取为 0.1,mm×0.2,mm×0.1,mm，格子数为 50×100×50，2个泥沙颗粒直径分别为 10,μm和 5,μm．在计算中保持颗粒不絮凝，并使之尽量靠近．图 1显示了衰减长度取不同值时颗粒间各种势能，图 1中的曲线表示公式计算值，离散点表示 LB模型模拟结果．从图中可以看出，模拟结果和公式计算值完全吻合．随着ABλ增大，A-B势能的作用范围与数值也增大，XDLVO总势能的势阱深度减小甚至消失，势垒高度增加，同时总势能的势阱位置和势垒位置都略有变大．该结果与文献[3]和文献[11]的模拟分析结果一致，说明LB模型中引进的XDLVO势是合理的．

图1 颗粒间势能和衰减长度的关系Fig.1 Relationship between the potential and decay length

2 黏土矿物对黏性泥沙絮凝影响的模拟分析

2.1 模拟参数设置

选取伊利土、蒙脱土和高岭土3种常见黏土矿物进行模拟分析，以检验基于 XDLVO理论所建立的LB模型是否反映了不同黏土矿物的絮凝特性．3种物质和水的相关参数见表 1[13-15]，计算中，水和颗粒密度分别为 1,000,kg/m3和 2,650,kg/m3，水的黏滞系数为 1.0×10-6,m2/s，重力加速度为 9.8,m/s2．模拟算例考虑重力作,用下做静水沉降的 2个泥沙颗粒，直径分别为10,μm和5,μm，初始时刻大颗粒位于小颗粒上方，两者垂向间距为2,μm，水平方向中心位置偏心距在0～4,μm间变动．

表1 计算参数Tab.1 Parameters in simulation

2.2 模拟结果分析

当两泥沙颗粒表面带有的束缚水层(滑动层)相接触，形成公共滑动层时，可认为颗粒结合而絮凝[16]，因此计算时以 2倍滑动层厚度作为泥沙絮凝的判断标准．图 2显示了不同算例中絮团的形成时间，图 3显示了沉降过程中颗粒的运动轨迹．由图2和图3可知：初始位置相同时，不同泥沙矿物发生絮凝的时间不同，伊利土最先发生絮凝，其次是高岭土和蒙脱土；泥沙矿物组成相同时，颗粒的初始位置影响其絮凝过程，两泥沙颗粒中心无偏离时，絮凝发生最早，偏心距离增大，絮凝出现时间延后，高岭土和蒙脱土在泥沙颗粒偏心距离为 3,μm 时不再发生絮凝，大颗粒绕过小颗粒后分别独自沉降，伊利土达到不絮凝的颗粒初始偏心距离为 4,μm．由此可知，就本文所取的3种黏土矿物而言，絮凝程度从易到难的顺序依次是伊利土、高岭土和蒙脱土．

图2 不同矿物成分的泥沙颗粒絮凝时间Fig.2 Flocculation time of sediment particles for different minerals

图3 颗粒运动路径Fig.3 Trajectories of particle settling

结合XDLVO理论，对沉降过程中泥沙颗粒的运动轨迹和受力进行分析，可以对上述过程做出合理的解释．以泥沙颗粒水平偏心距为 2,μm的情况为例进行分析，图4显示了3组黏土矿物泥沙颗粒间距的历时曲线，图5为图4的局部放大．图6显示了2个泥沙颗粒在沉降过程中的受力历时曲线，图中从上至下分别为水平和垂直方向作用力以及颗粒之间的XDLVO力．

两颗粒在距离较远(0.4,s之前)时，主要受到重力和周围流体运动引起的外力，XDLVO力的作用不明显，不同黏土颗粒其运动轨迹和受力状态基本相同．x方向上，大小颗粒之间表现为相互排斥，且排斥力随沉降时间增加而不断增大；y方向上，大颗粒受下方小颗粒尾流的影响，受力更为复杂，但大小颗粒之间仍表现为相互排斥．

图4 泥沙颗粒间距离历时曲线Fig.4 Time series of distance between particles

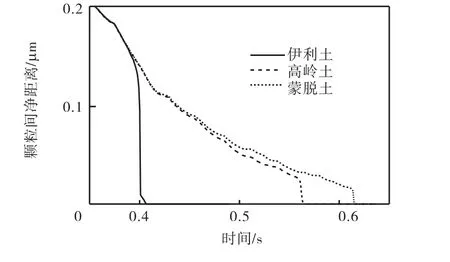
图5 泥沙颗粒间距离历时曲线(局部放大)Fig.5 Time series of distance between particles with local zooming

颗粒沉降 0.4,s后，随着颗粒距离减小，XDLVO力的作用开始明显，两颗粒之间的排斥力迅速减小直至变为逐渐增大的吸引力，颗粒间距离迅速变小，3种黏土颗粒先后发生絮凝．由表 1可以得知，伊利土的A-B自由能为负值，A-B力表现为吸引力，且其衰减长度大于其他2种矿物质，所以XDLVO力作用范围大，两个颗粒距离较远时颗粒间总作用力就表现为吸引力(见图5和图6(a))，因此容易发生絮凝．对于高岭土和蒙脱土，A-B力表现为斥力，且作用范围小，使得颗粒间总的作用力(吸引力)小于伊利土颗粒间作用力，且和伊利土的该力相比，作用距离小，作用时间晚(见图5、图6(b)和图6(c))，从而导致絮凝能力弱于伊利土．高岭土的 Hamaker常数大于蒙脱土，其颗粒间范德华吸引力大于蒙脱土；高岭土的AB自由能参数小于蒙脱土，其颗粒间 A-B斥力小于蒙脱土．因此，高岭土颗粒间 XDLVO力影响范围大于蒙脱土，絮凝时间较早，絮凝能力稍强．

对于同一种黏土矿物，泥沙颗粒初始位置无水平偏移时，两颗粒对心正碰，容易发生絮凝．若初始位置水平偏心不大，运动过程中颗粒间最小距离在XDLVO力的作用范围内，且吸引力大于排斥力，合力的作用仍会使泥沙颗粒形成公共滑动层，从而发生絮凝现象．当偏心距离大到两颗粒运动过程中其最小距离大于XDLVO力的作用范围，或者吸引力小于排斥力时絮凝现象就不发生．由于伊利土的 XDLVO力的数值和作用范围都较高岭土和蒙脱土大，因此其不发生絮凝的偏心距离大于后两者．

总的来看，图3～图6所输出的模拟结果充分反映了黏土颗粒在水体中沉降发生絮凝的变化过程．文献[17-18]分别通过物理实验得出伊利土絮凝能力高于高岭土和高岭土絮凝能力高于蒙脱土的结论，并解释了其絮凝机制．本文的模拟结果和上述实验结果一致，可以认为本文所建立的模型能够从颗粒之间相互作用的微观动力角度描述颗粒之间的絮凝过程，较好地反映了不同黏土矿物的絮凝特性．

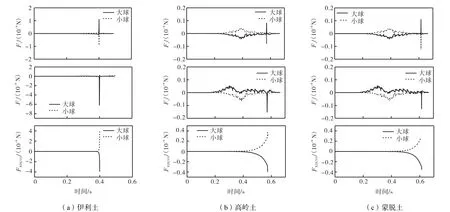
图6 不同矿物组分的泥沙颗粒受力历时曲线Fig.6 Time series of forces between particles for different minerals

3 结 论

(1)考虑XDLVO力的格子Boltzmann模型能够较好地模拟黏性泥沙的絮凝沉降以及该过程中颗粒之间的受力情况，从微观水动力学角度反映了絮凝机理和规律，可以用于进一步研究各种因素对黏性泥沙絮凝的影响规律．

(2)不同的黏土矿物颗粒絮凝的难易程度不同，就本文模拟的3种黏土矿物而言，絮凝程度从易到难的顺序依次是伊利土、高岭土和蒙脱土，和以往的认识一致．

［1］ 洪国军，杨铁笙. 黏性细颗粒泥沙絮凝及沉降的三维模拟[J]. 水利学报，2006，37(2)：172-177.

Hong Guojun，Yang Tiesheng. 3-D simulation of flocculation-settling of cohesive fine sediment [J].Journal of Hydraulic Engineering，2006，37(2)：172-177(in Chinese).

［2］ 王 龙，李家春，周济福. 黏性泥沙絮凝沉降的数值研究[J]. 物理学报，2010，59(5)：3315-3323.

Wang Long，Li Jiachun，Zhou Jifu. Numerical study of flocculation settling of cohesive sediment [J].Acta Physica Sinica，2010，59(5)：3315-3323(in Chinese).

［3］ 张金凤，张庆河. 黏性泥沙不等速沉降絮凝的格子Boltzmann模拟[J]. 水利学报，2009，40(4)：385-390.Zhang Jinfeng，Zhang Qinghe. Lattice Boltzmann simu-lation for flocculation of cohesive sediment due to differential settling [J]. Journal of Hydraulic Engineering，2009，40(4)：385-390(in Chinese).

［4］ Zhang Jinfeng，Zhang Qinghe. Lattice Boltzmann simulation of the flocculation process of cohesive sediment due to differential settling [J].Continental Shelf Research，2011，31(10)：94-105.

［5］ 卢 昭. 盐度对黏性泥沙絮凝影响的格子波耳兹曼模拟研究[D]. 天津：天津大学建筑工程学院，2007.

Lu Zhao. Lattice Boltzmann Simulation for Effects of Salinity on Flocculation of Cohesive Sediment [D].Tianjin：School of Civil Engineering，Tianjin University，2007(in Chinese).

［6］ 程洪剑. 黏性泥沙不等速沉降絮凝的格子波耳兹曼模拟研究[D]. 天津：天津大学建筑工程学院，2008.

Cheng Hongjian. Lattice Boltzmann Simulation for Differential Settling Flocculation of Cohesive Sediment[D]. Tianjin：School of Civil Engineering，Tianjin University，2008(in Chinese).

［7］ Ladd A J C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation(Part 1)：Theoretical foundation [J].Journal of Fluid Mechanics，1994，271：285-309.

［8］ Nguyen N Q，Ladd A J C. Lubrication corrections for lattice-Boltzmann simulations of particle suspensions[J].Physical Review E-Statistical， Nonlinear，and Soft Matter Physics，2002，66(4)：1-12.

［9］ Somasundaran P. Role of surface phenomena in the beneficiation of fine particles[J]. Mining Engineering，1984，36(8)：1177-1186.

［10］ van Oss C J，Chaudhury M K，Good R J. The mechanism of phase separation of polymers in organic mediaapolar and polar systems[J].Separation Science and Technology，1989，24(1/2)：15-30.

［11］ 胡岳华，邱冠周，王淀佐. 细粒浮选体中扩展的DLVO理论及应用[J]. 中南矿冶学院学报，1994，25(3)：310-314.

Hu Yuehua，Qiu Guanzhou，Wang Dianzuo． Extended DLVO theory and its applications in flotation of fine particles[J].Journal of Central South Institute of Mining and Metallurgy，1994，25(3)：310-314(in Chine-se).

［12］ Wu W，Giese R F，van Oss C J. Stability versus flocculation of particle suspensions in water-correlation with the extended DLVO approach for aqueous systems，compared with classical DLVO theory[J].Colloids and Surfaces B：Biointerfaces，1999，14(1/2/3/4)：47-55.

［13］ Hoek E M V，Agrwal G K. Extended DLVO interactions between spherical particles and rough surfaces[J].Journal of Colloid and Interface Science，2006，298(1)：50-58.

［14］ Li Z，Giese R，van Oss C J. Surface thermodynamic properties of some illites[C]//Program and Abstracts for Clay Minerals Society，28th Annual Meeting. Houston，TX：the Lunar and Planetary Institute，1991：100.

［15］ Duran J D G，Ramos-Tejada M M，Arroyo F J，et al.Rheological and electrokinetic properties of sodium montmorillonite suspensions(I)：Rheological properties and interparticle energy of interaction[J]. Journal of Colloid and Interface Science，2000，229(1)：107-117.

［16］ 杨铁笙，熊祥忠，詹秀玲，等. 黏性泥沙悬浮液中颗粒表面滑动层厚度的计算[J]. 水利学报，2002(5)：20-25.

Yang Tiesheng，Xiong Xiangzhong，Zhan Xiuling，et al. The study on slipping water layers of cohesive sediment particles [J].Journal of Hydraulic Engineering，2002(5)：20-25(in Chinese).

［17］ 王毓华，陈兴华，胡业民，等. 磷酸盐对细粒铝硅酸盐矿物分散行为的影响[J]. 中南大学学报：自然科学版，2007，38(2)：238-244.

Wang Yuhua，Chen Xinghua，Hu Yemin，et al. Influences of phosphates on dispersion of fine aluminumsilicate minerals [J].Journal of Central South University：Science and Technology，2007，38(2)：238-244(in Chinese).

［18］ Tombacez E，Szekeres M. Surface charge heterogeneity of kaolinite in aqueous suspension in comparison with montmorillonite [J].Applied Clay Science，2006，34(1/2/3/4)：105-124.