磴口黄河特大桥0号块空间应力分析研究

胡正荣 陈 亮 王金枝

（1.中交第二公路勘察设计研究院有限公司 武汉 430056； 2.青海省高等级公路建设管理局 西宁 810000；3.武汉理工大学华夏学院 武汉 430223）

现代桥梁的宽度大，横截面形式多样，桥梁结构的受力状况复杂，平面分析的结果己很难反映桥梁的实际受力情况，传统的桥梁设计方法和理论需要改进。因此，在对全桥整体静动力完成之后，在技术设计阶段还需对一些结构和受力复杂的局部构造进行详细分析计算，查明结构细部受力情况，以便改进设计或施工程序，确保安全。采用悬臂浇筑施工的连续梁桥，O号块是整个结构体系中应力最复杂的部分，因此，围绕着0号块的空间应力分析而展开的研究工作是具有现实意义的。

尽管目前连续梁桥0号块各部位拟定的几何尺寸，与按照平面杆系计算的内力相比是很富裕的，但很多已经建成的连续梁桥0号块内不同程度地出现了许多裂缝，这正说明目前设计者对0号块的应力状态还缺乏准确的把握和了解，需要对此展开理论研究。

1 工程概况

内蒙古树林召至包头东兴公路磴口黄河特大桥主桥为55 m＋9×100 m＋55 m的变截面连续箱梁，桥址处南岸大坝顶桩号为K38＋120，北岸大坝顶桩号为 K43＋843，K43＋378.3～K43＋710为河槽，其余均为河滩。大桥与跨越京兰线的公铁立交桥连接在一起，两桥之间设置过渡墩。

主桥箱梁为变截面单箱单室箱梁，悬浇施工，支点梁高6.25 m，跨中梁高2.5 m，其间梁高按1.8次抛物线变化，箱梁顶宽12.5 m，顶板厚0.65 m，腹板在跨中厚0.4 m，支点处厚1.5 m，底板跨中厚度0.3 m，支点处厚度1.5 m，其间底板厚度按二次抛物线变化，两侧悬臂宽3.0 m，箱梁断面采用直腹板断面底板宽6.5 m。主桥箱梁为三向预应力混凝土结构，纵向预应力采用大吨位群锚体系，横向预应力采用大吨位扁锚体系，竖向预应力采用JL32高强精轧螺纹粗钢筋锚固体系。

2 0号块三维模型建立

另外对0号块的局部应力分析，主要过程是首先采用桥梁设计专用程序（一般为平面杆系有限元程序）对桥梁作整体计算，即计算出0号块截面在各荷载组合作用下的弯矩、轴力和剪力，再将其转化为空间分析模型边界面上的分布面力和节点集中力，然后再按空间有限元分析0号块的应力状况。

依据圣维南原理［1］，在确定计算模型范围时，必须使0号块两端面至模型边界之间有足够长的一段过渡区，才能保证0号块端面及内部的应力具有足够的精度。本文将箱梁的0号块、相邻的两个1号块构成的空间实体作为研究对象，具体见下图1。

采用Midas FEA大型有限元程序，建立了0号块的三维空间有限元模型［2］，节段的实体网格划分见图1。

本桥上部结构与桥墩为支座连接，因此本模型按照实际施工工况设立支座约束。通过对全桥的整体分析计算得到1号块前端截面上的弯矩、剪力和轴力，只要将其转化为1号块前端面上各个块单元的分布面力和各个节点上的节点力，就已将上述荷载对0号块应力的共同影响共同影响计入在内了［3］。

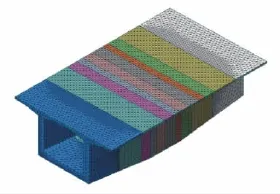
图1 有限元模型实体网格

由于箱梁0号块梁段在施工阶段、成桥和运营阶段的外荷载情况和边界条件均不相同，本文在箱梁0号块局部应力分析过程中考虑4种不利受力情况。

工况1。施工阶段最大悬臂状态箱梁0号块梁段的局部受力分析，考虑一端已经浇筑合龙段，而另一端尚未浇筑时的不平衡受力状态。

工况2。成桥阶段箱梁0号块梁段的局部受力分析，外加荷载为二期恒载。

工况3。运营阶段箱梁0号块梁段局部受力分析，外加荷载为二期恒载和汽车荷载，箱梁受到最大弯矩。

工况4。运营阶段箱梁0号块梁段局部受力分析，外加荷载为二期恒载和汽车荷载，箱梁受到最小弯矩。

3 0号块应力分析

3.1 应力计算结果

通过运用Midas FEA对0号块进行有限元分析，计算截面取3个，分别为0号块中心处、截面变化处、0号块端部，其划分见图2。

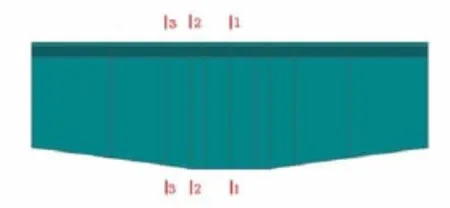
图2 计算截面示意

根据本文建立的桥梁模型计算可得出各计算截面在各工况下0号块的应力分布，从结果中依次提取该0号块在计算荷载工况作用下的横向应力、纵向应力、竖向应力、第一主应力、第三主应力的应力云图，本文受篇幅所限，且各工况发生应力集中的情况较为相近，故仅列出1－1截面在工况3作用下的纵向应力云图，见图3。各计算截面在各工况下0号块的应力最大值见表1。表中受拉为正，受压为负。

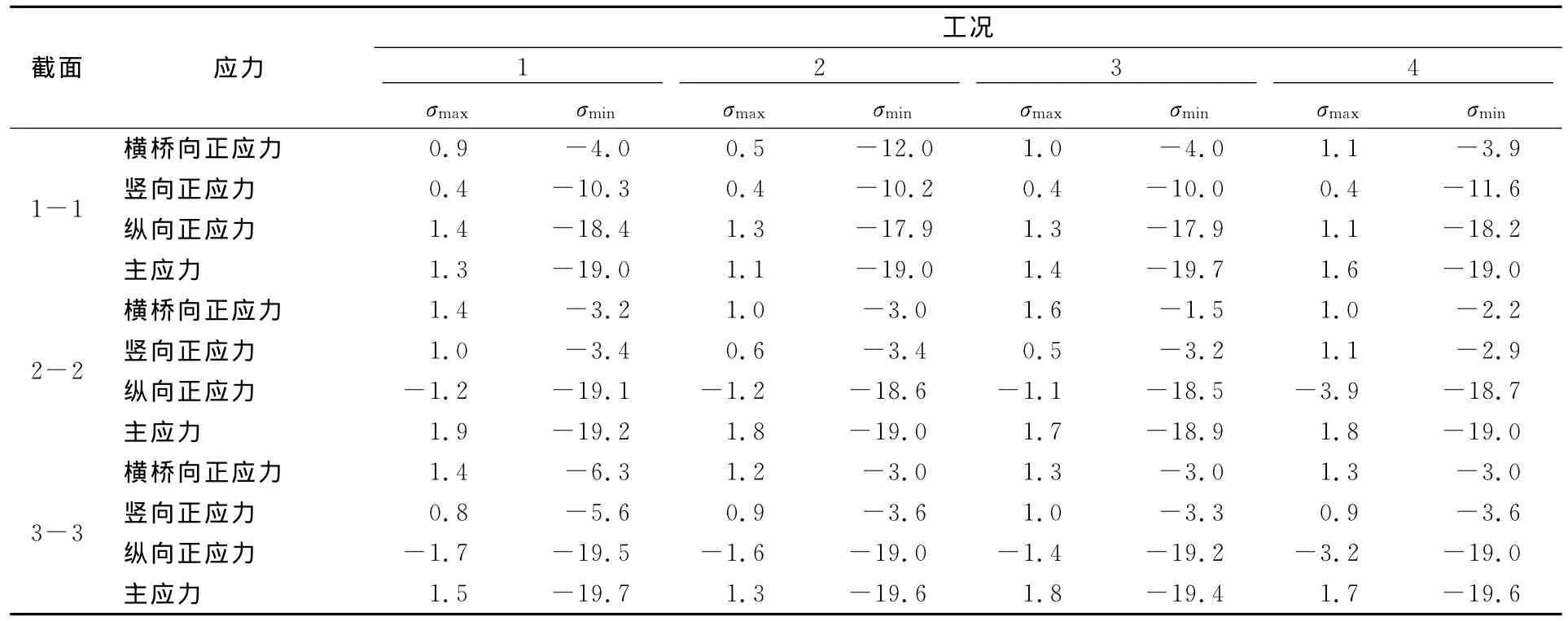
表1 应力分析表MPa

3.2 结果分析

通过以上应力计算结果可以看出：

（1）1－1截面处最大横向拉应力在运营（最不利）最小弯矩工况下为1.1 MPa，发生在1－1截面底部，靠近支座侧，在混凝土抗拉设计强度1.96 MPa范围内；竖向应力较小；最大拉应力在运营最不利）最小弯矩工况下为1.6 MPa发生在截面底部靠近支座侧；最大压应力在运营（恒载＋活载）最大弯矩工况下为19.7 MPa，出现在截面悬臂端部，此处为顶板横向预应力锚头位置，1－1截面应力满足要求。

（2）2－2截面处横向最大拉应力在运营（最不利）最大弯矩工况下为1.6 MPa，发生在2－2截面底部中间区域，在允许范围内，满足要求；竖向最大拉应力较小，满足要求；纵向最大压应力在最大悬臂工况下为19.1 MPa，发生在顶板纵向预应力锚头位置；最大拉应力在最大悬臂工况下为1.9 MPa，出现在顶板和腹板倒角处；最大压应力在最大悬臂工况下为19.2 MPa，出现在截面顶板位置，此处为顶板纵向预应力锚头位置，2－2截面应力满足要求。

（3）3－3截面处横向最大拉应力在最大悬臂工况下为1.4 MPa，发生在顶板和腹板倒角处；竖向拉应力较小；纵向最大压应力在最大悬臂工况下为19.5 MPa，发生在顶板纵向预应力锚头位置；最大拉应力在运营（最不利）最大弯矩工况下为1.8 MPa，出现在顶板和腹板倒角处；最大压应力在最大悬臂工况下为19.7 MPa，出现在截面顶板位置处，此处为顶板纵向预应力锚头位置，3－3截面应力满足要求。

线性杆件分析都是基于材料力学的平衡面假定的，因此横截面的法向正应力分布也是线性的。现以1－1截面在工况3下的纵向应力为例，根据材料力学公式可得1－1截面纵向的应力值，其中上下缘应力值分别为

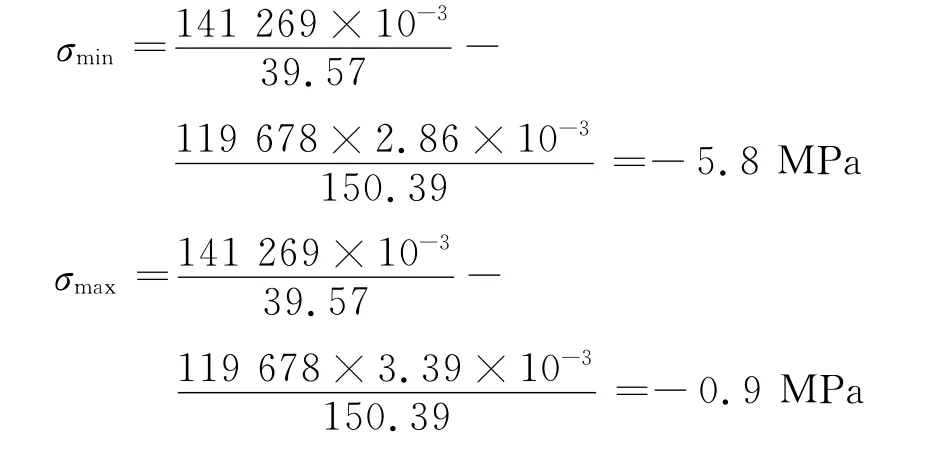
将上述计算结果与有限元计算结果相比较，见图3，其中虚线为材料力学计算结果。从中可看出箱梁截面的纵向应力不遵循线性变化规律，且存在明显的应力集中，应力集中系数可达3.1。因此，材料力学中的平衡面假定适用于细长梁，而连续梁桥的墩梁节点处由于外形突变将产生明显的应力集中现象，纵向应力不按平截面假定分布，必须进行局部应力分析。

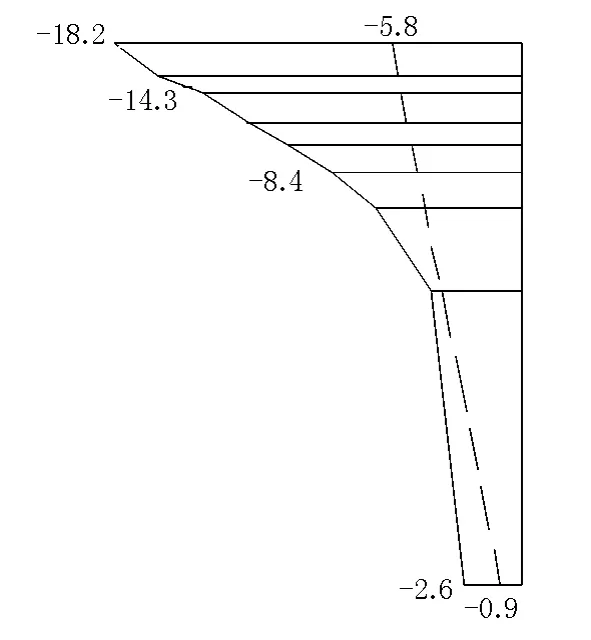
图4 纵向应力分布图（单位：MPa）

4 结论及建议

（1）通过1－1截面的应力分析，建议在1－1截面底部横向两支座之间的区域加强配筋；通过2－2截面的应力分析，建议应加强2－2截面底部中间区域的横向配筋；在截面顶板与腹板的倒角处应加强配筋，同时还应该尽量将结构倒角和转折处做得圆顺平滑，避免尖角出现，使应力集中现象得以缓和，以改善0号块的受力性能。通过3－3截面的应力分析，在顶板中部、腹板和底板倒角区域处应加强配筋，同时还应该尽量将结构倒角和转折处做得圆顺平滑，避免尖角出现，使应力集中现象得以缓和，以改善0号块的受力性能。

（2）箱梁顶板范围内压应力普遍较大，接近20 MPa，建议优化这部分区域结构尺寸或调整纵向预应力型号，来减少这部分区域内的压应力。桥的三向预应力加载后，截面的最大拉应力、最大压应力都明显减小，同时要注意到，在少数节点处，如1－1截面顶板下缘反而会出现纵向拉应力，这是由于加载位置在1号块端部以及泊松效应的结果。

［1］ 肖 礼，彭文立，秦 荣.圣维南原理在钢管混凝土拱桥分析中的应用［J］.中国公路学报，2001，14（2）：33－35.

［2］ 夏 勇，裴若娟.广珠准高速铁路东海西江大桥0号块空间分析［J］.桥梁建设，1997（4）：74－77.

［3］ 戴 维.悬灌箱梁0号块及1号段裂缝整治［J］.世界桥梁，2003（2）：70－72.