移相全桥变换器电压模式控制器的设计与仿真

张涛，刘胜道，祝小雨



移相全桥变换器电压模式控制器的设计与仿真

张涛，刘胜道，祝小雨

（海军工程大学电气工程学院，武汉 430033）

本文设计了一款ZVS移相全桥变换器，给出了移相全桥变换器的小信号模型。在小信号模型基础上，采用Matlab软件设计了电压模式控制器。最后采用Saber软件对系统进行了仿真。仿真结果表明电压模式控制器是可行的，系统能够正常运行。

移相全桥变换器 电压模式控制 Matlab Saber

0 引言

在开关电源的设计与研发中，开关变换器控制系统的设计是非常重要的一个环节，它的好坏直接决定着电源的性能和质量。目前主要的控制方式有电压模式和电流模式两种，电流模式补偿简单，环路响应快，但是它的数学模型比较难得到；电压模式补偿稍复杂，但是它的数学模型比较容易得到[1]。本文采用电压模式控制，在移相全桥变换器小信号模型的基础上设计了电压模式控制器，并用Saber软件进行了仿真，仿真结果表明电压模式控制器是可行的。

1 ZVS移相全桥变换器参数

本文设计了一款ZVS移相全桥变换器，并进行了仿真实验。全桥变换器采用UC3875N芯片控制，其主要参数如下：输入直流电压in=220～360 V，额定输出电压o=25 V，变压器副原边匝比=1/6，开关频率=50 kHz，谐振电感及变压器漏感r=8.18mH，输出滤波电感=25mH，滤波电容=500mF，等效串联电阻（ESR）c=0.13 Ω，负载电阻=0.25 Ω，基准电压ref=2.5V，UC3875N的PWM锯齿波峰值M=3.23V。

2 移相全桥变换器小信号模型

状态空间平均法是变换器小信号建模的一个常用方法。文献[2]给出了ZVZCS移相全桥变换器的小信号等效电路模型和主电路控制-输出的传递函数。ZVS移相全桥变换器的小信号等效电路模型和控制-输出的传递函数与ZVZCS类似，可得ZVS移相全桥变换器控制-输出的传递函数vd(s)：

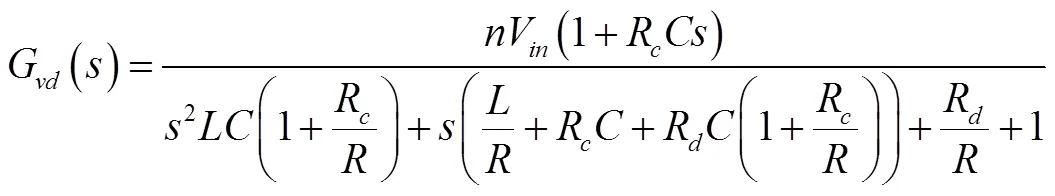
其中：d=2Lf

3 电压模式控制器的设计

电压模式控制的基本思想：输出电压经采样后与给定的基准电压相比较，所得的误差送补偿放大环节，再经脉冲宽度调制，得到一系列控制用的脉冲序列，控制变换器中功率开关器件的通断，达到稳定输出电压的目的。通常，把补偿网络和电压采样网络合并，称为电压模式控制器，把电压模式控制器之外的环节称为控制对象[3]。

图1是电压模式控制原理框图：G()是主电路控制-输出传递函数，M()是PWM传递函数，()是电压采样网络的传递函数，c()是补偿网络传递函数。

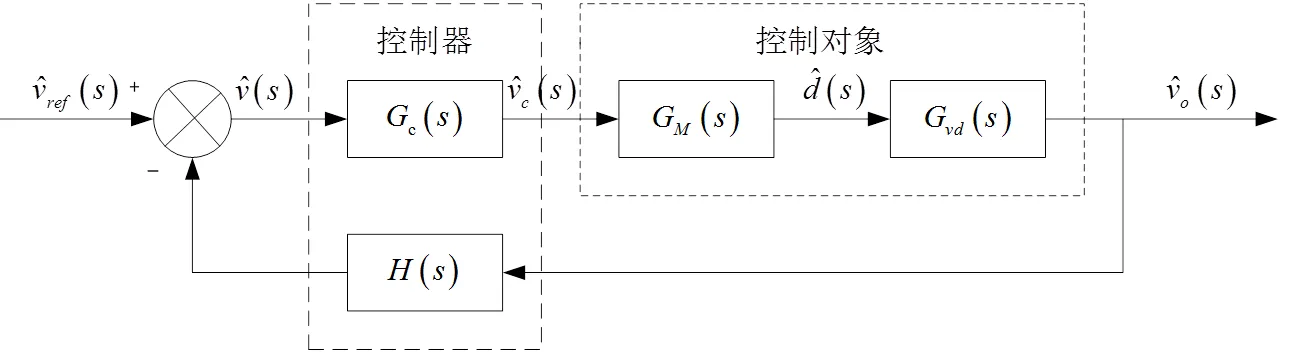
图1 电压模式控制原理框图

要设计反馈回路使闭环系统稳定，必须先求出系统的开环传递函数。将ZVS移相全桥电路参数代入（1）式，得到主电路控制-输出的传递函数G()：

PWM传递函数M()=1/M=1/3.23，电压采样网络的传递函数()=ref/o= 2.5/25，可得系统未补偿前的开环传递函数G()：

采用Matlab软件对未补偿前开环系统进行频域分析，系统开环波特图如图2所示，未补偿前开环系统的相位裕量101°；低频段增益约3.95 dB，过小；穿越频率为1.66 kHz，过小，开关电源的穿越频率一般应设置为开关频率的1/10-1/5；系统增益过ESR零点后以-1的斜率下降，抗高频干扰能力较弱。因此，需要进行补偿。

常用的补偿网络有三种，分别称为1型、2型和3型。1型补偿网络只有一个零点，只能用于电流模式控制；3型补偿网络功能最强大，但是网络复杂，设计比较麻烦；对于一般的电路，2型补偿网络已经够用[1]。本文采用2型补偿网络进行校正，2型补偿网络有一个零点，两个极点，其中一个是零极点，如图3所示：图中R1与R3组成电压采样网络，R1既是电压采样网络的一部分，也是2型补偿网络的一部分，R3不属于2型补偿网络，故采用虚线表示。

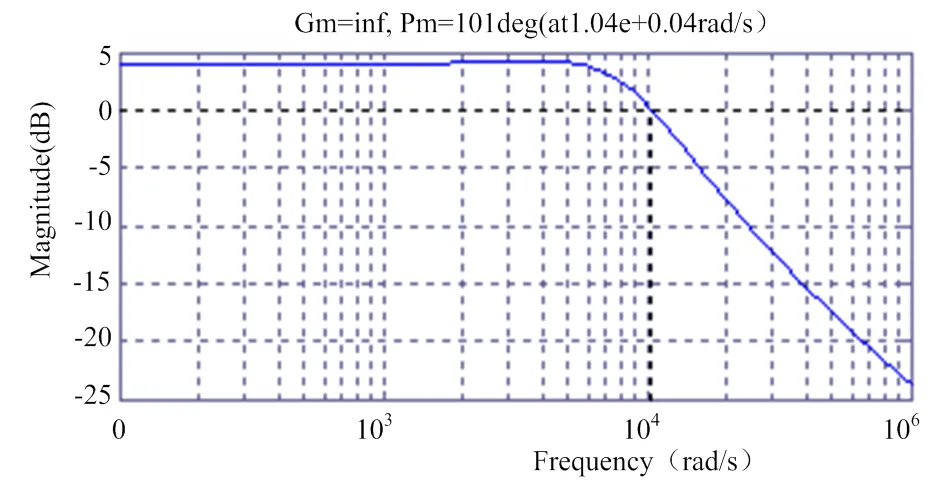
图2 未补偿前系统开环波特图

2型补偿网络传递函数c()：

利用2型补偿网络进行补偿时，我们将穿越频率设置为开关频率的1/10，即5 kHz。一般情况下将2型补偿网络的零点配置在LC双重极点附近，将高频极点配置在ESR零点附近，然后再利用Matlab进行优化，最终得到2型补偿网络传递函数Gc(s)：

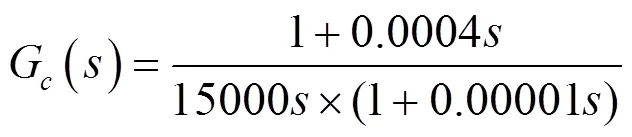
补偿后系统开环波特图和闭环阶跃响应曲线如图4所示，低频段增益明显增大，穿越频率为6.13 kHz，幅值裕量无穷大，相位裕量为59.3°，高频段以-2的斜率快速衰减，抗高频干扰能力强。系统调节时间约0.591 ms，超调量约10%，系统能迅速稳定运行。

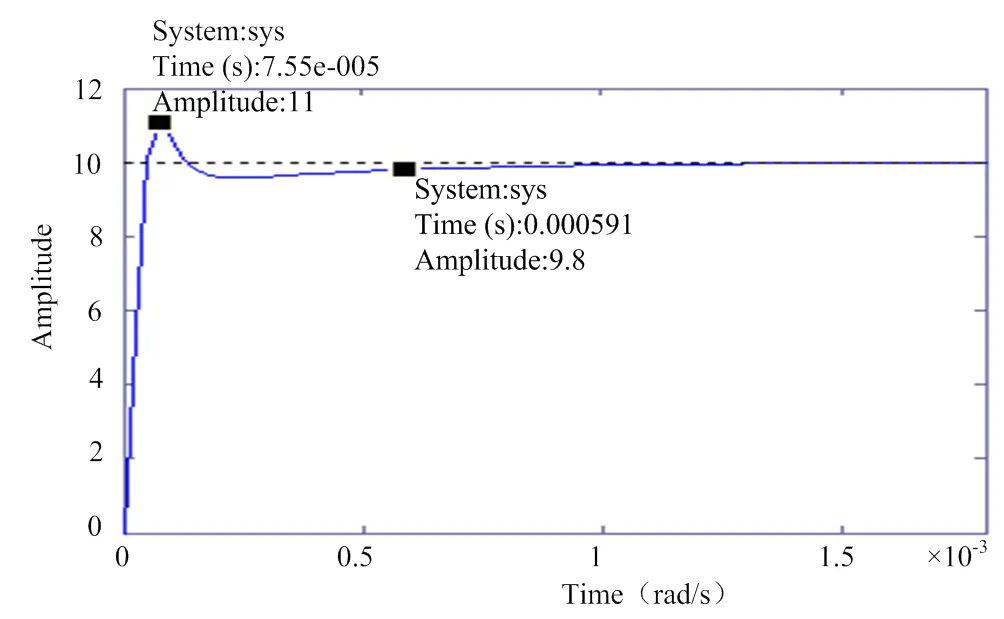
图4 补偿后系统开环波特图和闭环阶跃响应曲线

电压采样网络采用电阻分压网络，由1/3=o/ref-1=9知，可取1=9 kΩ，3=1 kΩ。经计算：2=54 kΩ，1=18.5 pF，2=7.4 nF，即可得到电压模式控制器。

4 仿真实验

本文采用Saber软件对系统进行仿真，主要模拟输入电压波动和负载电阻突变对系统的影响，具体参数设置如表1。

表1 参数设置表

仿真结果如图5所示，Vin曲线表示输入电压，Vo曲线表示输出电压，从图中可以看出输入电压波动对系统基本无影响，负载电阻突变会导致系统出现短暂不稳定，但很快又回到稳定状态。仿真结果表明，本文设计的电压模式控制器是可行的，电路能迅速稳定运行。

5 结论

本文在移相全桥变换器小信号模型的基础上设计了电压模式控制器，并进行了仿真。仿真结果表明，电压模式控制器是可行的，系统能迅速稳定运行。由于条件限制，未进行实际的电路实验。在实际的电路中，由于输出电容的串联等效电阻不是定值，会受线路长度、温度、使用时间等因素影响而变化[1]。因此，实际中要在理论设计的基础上反复进行调试，得到一个最佳的参数。

[1] （美）马尼克塔拉（Maniktala,S.）著；王志强等译. 精通开关电源设计[M]. 北京：人民邮电出版社, 2008: 183-223.

[2] 陈咸丰. 移相控制ZVZCS全桥变换器的研究与应用[D]. 南京：河海大学硕士论文，2006: 13-19.

[3] 张卫平. 开关变换器的建模与控制[M]. 北京：中国电力出版社，2005: 1-31，124-130.

[4] 黄忠霖，周向明. 控制系统MATLAB计算及仿真实训[M]. 北京：国防工业出版社, 2006: 223-233.

[5] 陈国超，张昆仑. 移相全桥ZVSZCS双闭环控制系统设计[J]. 通信电源技术, 2010, 27(5): 20-23.

Design and Simulation of Voltage-mode-controller of Phase-shift Full-bridge Converter

Zhang Tao, Liu Shengdao, Zhu Xiaoyu

（College of Electric Engineering, Naval University of Engineering, Wuhan 430033, China）

TM461

A

1003-4862（2013）10-0028-03

2013-02-25

张涛（1984-），男，硕士研究生。研究方向：电磁环境与防护技术。