反应堆净化系统的模糊多状态可靠性分析

2013-04-30朱康赵新文

船电技术 2013年8期

朱康，赵新文

反应堆净化系统的模糊多状态可靠性分析

朱康，赵新文

（海军工程大学，武汉 430033）

针对反应堆净化系统的多态特征，考虑到净化系统中多态部件的状态性能以及状态间转移率的模糊性，为克服由此引入的不确定性，运用模糊发生函数法进行了研究。建立了多态部件备用系统的状态转移模型，求取了净化系统处于不同性能水平的水平截集区间。表明模糊通用发生函数法能够解决上述因素而引入的不确定性。

净化系统模糊发生函数法多状态可靠性

0 引言

传统的可靠性理论建立在系统部件处于二元状态的假设之上，是对复杂系统状态的简单描述[1]。近年来，随着对系统失效机理和规律逐渐深入地研究，系统的多态特征逐步得到了重视，并由此产生了多状态可靠性理论。本文针对反应堆净化系统中多态部件的状态性能以及状态间转移率的模糊性，运用模糊发生函数法[2]对其进行了研究。

1 方法建模

根据图1可得到模糊多状态元件所对应的微分方程组如下所示：

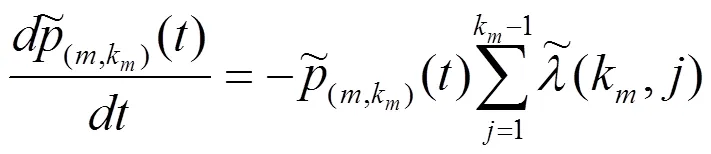
（3）

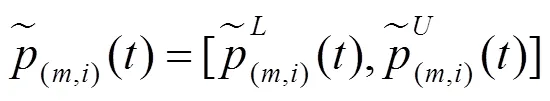
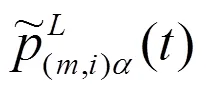
图1 模糊多状态元件m的状态空间图

为计算模糊多状态系统的可靠度，Ding等定义了相对基数[2]，记为：

本试验标本采集于威宁县草海国家级自然保护区水质保持相对较好的阳关山水域，总共采集样本408条，分两个不同的季节采样，2016年7月和2017年3月各采集一次。由于云南鳅个体比较小，样本采集时主要通过地笼进行捕获，将地笼定置在水草繁茂水质相对较好的地方，第2天收网，并将云南鳅与其他的渔获物分离出来，现场把样本用8%的甲醛溶液固定保存，带回实验室处理。

图2 模糊状态性能与模糊任务需求性能的重叠现象

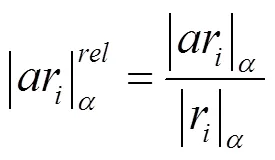
两部件备用系统的主设备和备用设备之间存在备用逻辑关系，它们不是独立的。设备用系统有两个部件A、B，每个部件都有三个性能指标：0表示完全失效；0.8表示部分失效；1表示正常运行。各个元件的性能状态以及状态转移率以模糊数形式来描述。假设备用系统正常工作时，主设备工作，备用设备备用且只有当主设备完全失效时备用设备才投入运行。其状态转移图如图3所示。

在图3中备用系统的部件不可修，共有5个状态：状态0：主设备正常运行，备用设备备用；状态1：主设备部分失效，备用设备备用；状态2：主设备完全失效，备用设备投入运行；状态3：主设备完全失效，备用设备部分失效；状态4：主设备、备用设备都完全失效。对该并联备用系统建立状态转移方程组：

初始条件为：

根据参数规划，可以分别求得各个模糊状态概率的水平截集区间。

2 实例分析

反应堆净化系统由净化泵、热交换器、离子交换器、过滤器及相关阀门和管路构成[3]。其中2台净化泵具有备用关系。来自主冷却剂系统的冷却剂由2台处于并联备用关系的净化泵加压后经2台热交换器冷却进入离子交换器，再经再生式热交换器进入主回路。其系统图如图4所示。

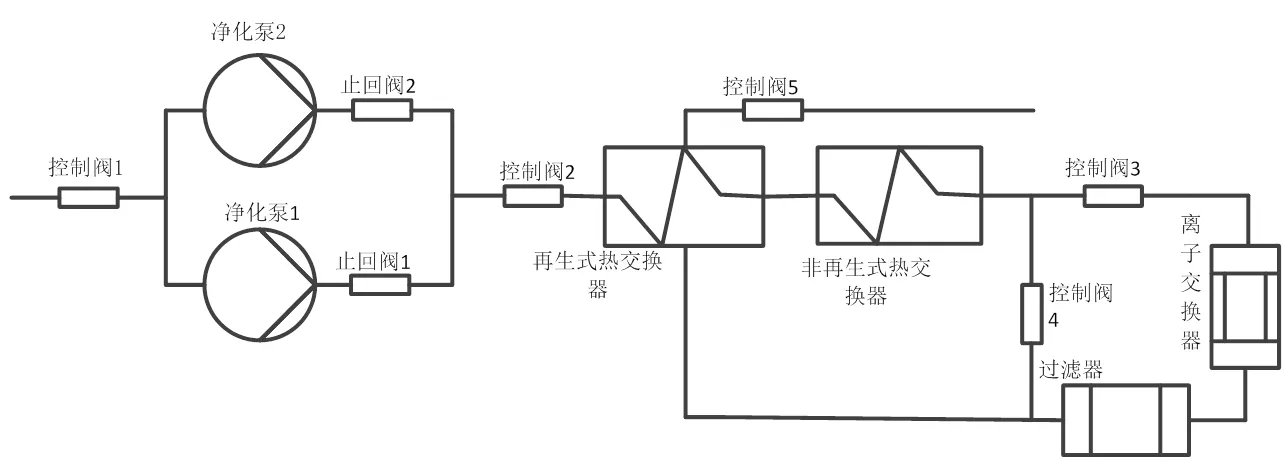
图4 反应堆净化系统图

在图4中控制阀3、4为电磁阀，它们的作用是：位于非再生式热交换器后的温度传感器在检测到水温高于离子交换器工作温度时，通过控制阀3、4的动作隔离离子交换器。冷却剂经净化系统净化后，里面的可溶性和不可溶性杂质都被清除，确保主回路的冷却剂水质洁净，降低冷却剂的放射性水平。控制阀4是常闭阀门，它和阀3的作用是保证离子交换器的工作安全，当从非再生式热交换器流出的冷却剂温度高于设定值时，控制阀3关闭，控制阀4开启，只有当控制阀4关闭，控制阀3开启净化系统才发生作用。控制阀3、4可以看作是串联关系。止回阀1和止回阀2在系统运行时一直处于工作状态。一个止回阀有流体流过时，另一个止回阀就起到止回的作用。所以只要有一个止回阀发生故障，系统就会发生故障。

在反应堆净化系统中，考虑净化泵性能水平的退化，将其视为多态部件。由于性能退化数据的缺乏，将其状态性能及状态转移率以三角模糊数形式描述，如表1、表2所示。

表1 净化泵模糊状态转移率（单位：1ｘ10-4/h）

在表2中各状态的性能表示为净化泵处于不同状态时对整个净化系统正常工作性能的贡献比率。其中状态2具有最高的性能，状态0完全失效，状态1的性能介于状态0与状态2之间。

表2 净化泵模糊状态性能

在净化系统中，两台净化泵属于备用关系，利用式(13)到式(17)即可求得其模糊发生函数。净化系统中其他部件为二态部件，其性能指标为：0表示完全失效；1表示正常运行。失效数据[4]如表3。

根据表3中的数据，可相应地求出净化系统中二态部件的发生函数。根据模块化方法[5]对图4所示的反应堆净化系统图进行简化，如图5所示。

表3 净化系统部件失效数据

图5 反应堆净化系统模块简化图

在图5中模块1表示控制阀1、4、5、11串联组成的子模块；模块2表示处于备用关系的净化泵组成的子模块；模块3表示在逻辑上具有串联关系的止回阀2、3组成的子模块；模块4表示处于串联关系的热交换器6、7组成的子模块；模块5表示在逻辑上具有串联关系的控制阀8、9组成的子模块；模块6表示处于串联关系的离子交换器和过滤器组成的子模块。在求出各个子模块的发生函数后，利用通用发生函数的递归算法即可求得反应堆净化系统的发生函数及其处于各个性能指标时所对应的概率，图6、图7给出了净化系统部分失效和正常工作时的水平截集区间（=0）。

图6 净化系统正常工作概率

图7 净化系统中间状态概率

图8 净化系统在t=1000 h的可靠度隶属函数

利用图8所示的隶属函数可求得净化系统在不同隶属度情形下的可靠度区间，例如，0.1时，可靠度区间为[0.68,0.86]，0.6时，可靠度区间为[0.73,0.81]。需要注意的是，当水平截集为1时，所有元件的状态转移率、状态性能以及系统的任务性能需求水平均变为精确值，按照传统的方法即可求出系统的可靠度。