埃舍尔的“不可能”的画

蒋明玉

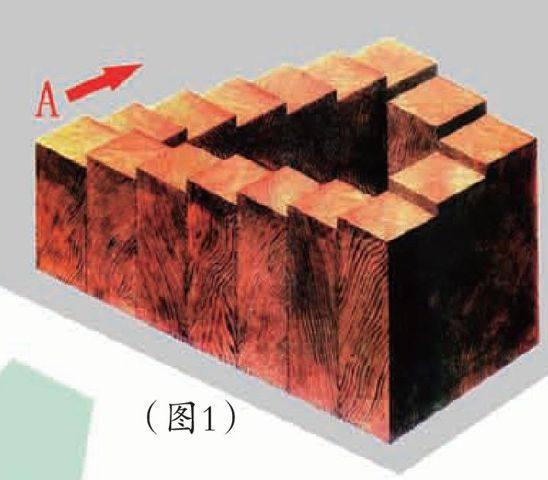
大家请看图1，可能你会觉得这是一个很普通的台阶图，那么请你想象一下，假如你站在A点的台阶上往下走，走到底以后再右转弯往下走，你会发现什么？把你的发现和其他人交流一下，再想一想，生活中会有这样的“台阶”吗？为什么在这幅图上会觉得这样很“正常”呢？

说到这种实际“不可能”出现的画，首先要向大家介绍一下拥有许多数学家知音的荷兰大画家莫利茨·柯尔内留斯·埃舍尔。他曾经这样说过：“我在阳光中所描绘的形象，只不过是我在暗中所见到的百分之一。”这倒是道出了他的作品的特点——荒谬和真实的统一！确实，他以自己的智慧向世人展示了“不可能”的画，他那深刻的思想就蕴含在这些画中。

让我们看一下他的那幅以“怪圈”为主题的版画《上天入地》（如图2），这是一幅带有浓厚宗教色彩的画。让人奇怪的是，回廊上的僧侣排成了两队往前走，其中一队总是沿着楼梯向上走，可是却总能回到原地；另一队总是沿着同样的楼梯向下走，也总能回到原地。像这种从一个地方出发，一步一步地上升，或一步一步地下降，结果却意外地又回到原来起点的现象，叫作怪圈。

荒诞画与视错觉是一对孪生子。埃舍尔还有一幅名叫《瀑布》的画（如图3），也是一个“怪圈”，塔楼上泻下来的一道瀑布，推动了磨坊的水轮，可是下面盛水池中的水流过水槽，居然又回到了瀑布的源头！大家想一想，这个问题出在哪里？

埃舍尔创作《瀑布》的灵感来自英国理论物理学家彭罗斯构想的“不可能三杆”（如图4）。彭罗斯把它叫做三维直角结构：三个直角都很正常，但它们是以错误的、在现实中根本不可能的方式连接起来的，于是就形成了这样一个三角形，三个角之和为270度——当然它肯定不是任何实际存在的空间结构的投射。

彭罗斯把这样的“不可能三杆”连接起来，从图中看到，我们沿着从A点走到B点是平坦，从B点到C点似乎也是平坦的，但如果从 C点回到A点，在视觉上我们却兀地掉了下来。这正是埃舍尔在《瀑布》中所达到的效果，而这一切只是因为构成图形的每一个三杆都是不可能存在的。

下面这幅石版画《观景楼》（如图5）也很有名。稍加注意你就会发现，这个亭子建得很怪异。亭子的上层与下层居然互成直角！此外，把两层楼台连接起来的八根柱子也很奇怪。只有最右边和最左边的柱子是正常的，其余六根都是内外交错，它们会从中央的空间斜穿而过。这就造成了另一个更加荒谬的图景：那架竖得笔直的梯子，它的最上端斜靠在观景楼的外边，而梯脚却站在楼内。如果我们把画面从中间沿水平线剪开，就会发现两个部分都很正常。那么不言而喻，视觉上的悖谬来自于两个部分的错误的连接，即上面已经提到的六根柱子的不可能的连接。其实，埃舍尔只不过严密地利用了数学表现的方法。这种有效地利用不可能的自然现象和数学的严密性创造的版画，实在令人吃惊。

埃舍尔不仅是位艺术家，还是艺术家里的思想者。这些“好玩”的绘画事实上包含了他对绘画本质的更深刻的思考。他很早就意识到所有绘画先天具有的矛盾——那就是三维的空间必须表现在二维的平面上。因为这个内在的矛盾，他认为任何绘画都是一种自欺欺人的骗术。既然如此，就可以通过对传统透视法进行革新，在平面上营造出在三维空间中都不可能存在的世界，把观者骗得更甚。

你能自己动脑创作一幅不可能的画吗？如果画好了，记得寄给我欣赏哦。