数学教学要有“序”

刘晓山

“数学是思维的体操。”“数学是一门具有高度抽象性和严谨逻辑性的学科。”“数学是一个培养学生逻辑性思维的学科。”……从这些表述中不难看出一个共性，那就是数学离不开逻辑，离不开内在的“序”。既然逻辑作为数学这门学科的特质，那么作为数学的教学也自然离不开逻辑，离不开蕴含其中的“序”。为此，作为数学教师的我们在进行数学教学时，一定要考虑到其内在的逻辑性，一定要梳理出其内在的序列。

一、以生活为“序”，让学生激活知识图库

“生活是数学的源泉。”既然数学与生活的联系如此紧密，作为数学教师的我们就应基于学生已有的生活经历，找寻数学与学生生活经历的联系，将逻辑性很强的数学内容激活，从而实现数学与儿童认知世界的交汇。

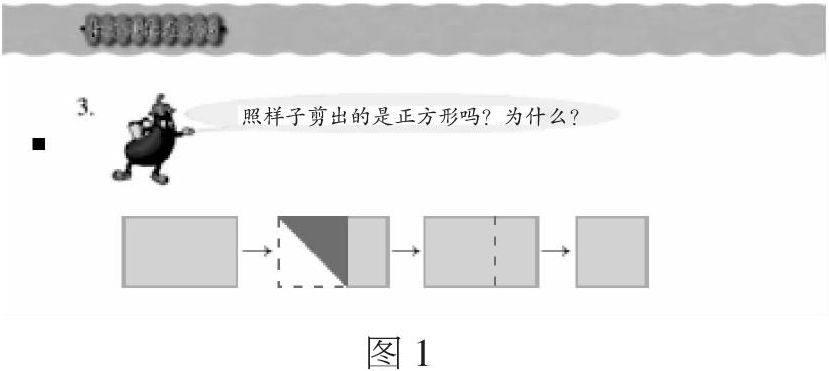
例如《长方形和正方形的认识》练习题：

教学时，如果让学生照着插图的样子进行折叠，并让他们直接说出答案，虽然学生也能回答，但在他们的认知体系里，或者是思维的潜意识里并不能认同这一结果。这是因为单纯地依靠这一折纸过程，学生很难找寻出它们内在的联系。为此，我基于学生的生活经历，即做大风车等手工的经历设计这样几个步骤：首先出示一张长方形的纸，要求学生将这张纸变成可以折大风车的纸；在学生归纳出大致方法后，接着以“为什么”为切入点，让学生探讨其中的原因；当学生明白了这样折叠（如图1）是保证纸的长与宽相等后，我再提供两张大小不同的纸，提问：“哪一张纸能折出更大的正方形？”进一步让学生明白：折叠后的正方形的大小是由原来长方形的宽决定的。这样，基于学生的生活经验，将书本知识有效链接到学生认知图库，就能让学生更好地生成数学思维，提升数学能力。

二、以经验为“序”，给学生提供方法借鉴

数学教学除了培养学生的数学思维、数学视角，还要培养学生利用数学知识来解决实际问题的能力。在具体的教学中，教师不能简单地进行空洞的说教，而要引导学生从已经生成的经验中找寻、建构解决问题的简单路径，从而让学生习得具体方法的同时，也能贯通数学的思维。

例如四年级数学下册《乘法》中的例题 “回收1 吨废纸可以造出850 千克再生纸，同时还节省化工原料300 千克，节约电600 千瓦时，节约水100 吨。（1）某废品回收站上个月回收废纸36 吨，用这些废纸能造出多少千克再生纸？（2）你还能提出什么问题？”单就这个题目而言，信息量是很大的，如何让这个题目简单些？如何让学生掌握解决此题的方法？首先将此题转接到学生的生活经验上，如一元钱可以买4个橡皮、2个包子，那么两元钱可以买到什么？ 之后将各种信息用表格整理如下：

有了这样的经验转接，学生不仅很轻松地了解了此题的主旨，他们还能针对要求提出了很多问题，有数学的，有环保的。我想，学生之所以能产生这样的学习激情，形成这样的方法能力，是因为教学基于学生的经验，并以此为教学的突破口。

三、以图像为“序”，为学生呈现思维支撑

数学中的关系纷繁复杂，既包括数量关系，又包括空间位置，还包括事情发展与出现的概率……擅长形象思维的小学生面对这些数学知识时，常常有一种“丈二和尚摸不着头脑”之感。此时，作为教师的我们就可以借助有形媒介——图形，让繁杂抽象的关系形象化、浅显化、条理化，从而为学生呈现出必要的思维支撑。

例如三年级下学期《找规律——植树问题》的教学。如何让学生一目了然地感知植树、锯木料、爬楼梯等问题中的规律？我首先将这些问题以“示意图”的形式呈现出来，有了这些示意图，学生就能理解其中的规律：如段数在两端，比锯的次数多一个；层数在两端，比楼梯数多一个……有了图形，学生就能很好地建构起实际问题的规律图式。（注：锯木料问题（图2-1），楼梯问题（图2-2），发车问题（图2-3））

总之，当教师以逻辑的视角，以生成的规律，以数学的思维组织教学时，学生的思维就会变得有“序”。

（责编 金 铃）