基于相似度原理的船舶电力推进系统仿真可信度研究

刘建波



基于相似度原理的船舶电力推进系统仿真可信度研究

刘建波

（海军驻上海江南造船集团有限责任公司军事代表室，上海 201913）

为了更好地检验船舶电力推进系统仿真的可信度，结合相似度原理和模糊综合评判方法，对船舶电力推进系统的定性与定量指标进行综合分析。将影响系统仿真的可信性因素综合起来建立评价指标体系，并依据层次分析法原理确定各指标的权重向量。针对专家所给的权重判断矩阵，进行次序一致性检验和基本一致性检验。确定子系统隶属函数。验证仿真系统可信性分析方法的可行性，并取得了较好的结果。

船舶电力推进系统 模糊综合评判 相似度 可信性分析

1 评价指标体系的建立

随着仿真技术的不断发展和船舶电力推进系统的广泛应用，必需对船舶电力推进系统仿真进行可信性分析。研究船舶电力推进系统仿真可信性时，首先需要确定系统仿真的评价指标体系。

船舶电力推进的系统仿真在建立时，首先需要确定系统的概念模型，然后通过计算机语言建立系统的计算机模型，确定计算机模型时需要系统的相关参数。最后通过系统的仿真结果进行分析。依据指标评价体系的建立原则，选择如下指标分析船舶电力推进系统仿真的可信性。本文只给出三层评价指标体系。

1) 系统仿真模型；

2) 系统仿真结果；

3) 数据有效性。

根据以上分析，建立船舶电力推进系统仿真可信性分析的评价指标体系。具体如图1所示。

2 可信性分析评价方法

船舶电力推进系统仿真可信性分析的评价指标体系中，有的指标类型为定量的，有的则为定性的，不能采用单一的评价方法进行分析。模糊综合评判是通过专家打分对系统进行分析，相似度原理是依据各指标的仿真数据与实际数据或期望数据分析其相似度。鉴于船舶电力推进系统仿真可信性分析评价指标体系为分层次的，在评判过程中需要考虑各指标在综合评价过程中的权重大小。因此，根据模糊综合评判和相似度原理的特点，结合层次分析法原理，对船舶电力推进系统的仿真可信性进行综合分析。

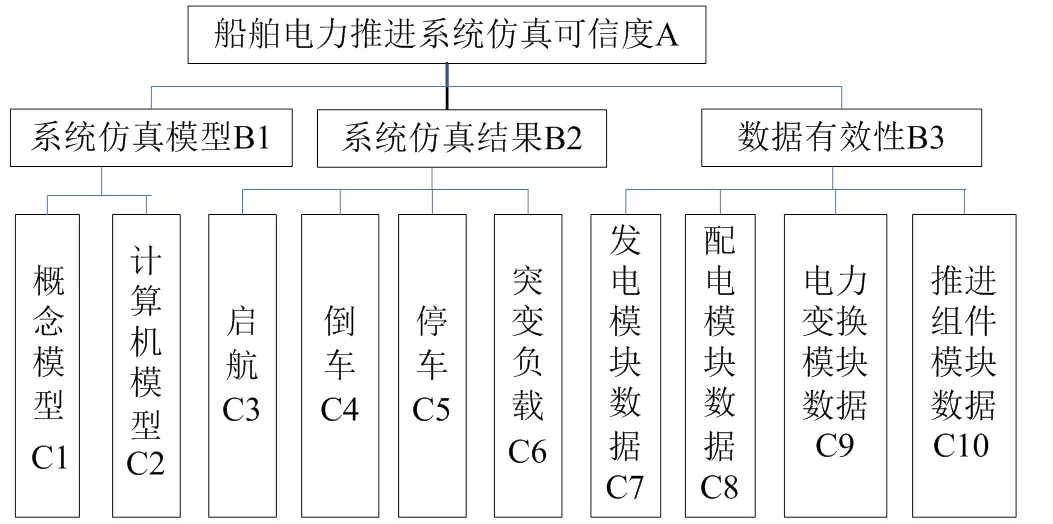
图1 船舶电力推进系统仿真可信性分析评价体系

整个船舶电力推进系统的仿真可信性分析过程如下：

1) 依据系统相关标准及评价指标体系建立原则，建立评价指标体系。

2) 利用层次分析法原理，确定各指标在综合评判过程中的权重大小。

3) 结合模糊综合评判原理和相似度原理法，对船舶电力推进系统仿真进行可信性分析。

2.1 层次分析法原理

分析船舶电力推进系统的仿真可信性时，需要确定各指标在评判过程中所占的权重大小[1]。

1) 利用层次分析法原理求取指标权重时，首先需要专家给出各指标相对于上层指标的相对重要性，也即判断矩阵。专家给出指标的判断矩阵依据互反性1-9标度表。具体如表1所示。

表1 互反性1-9标度表

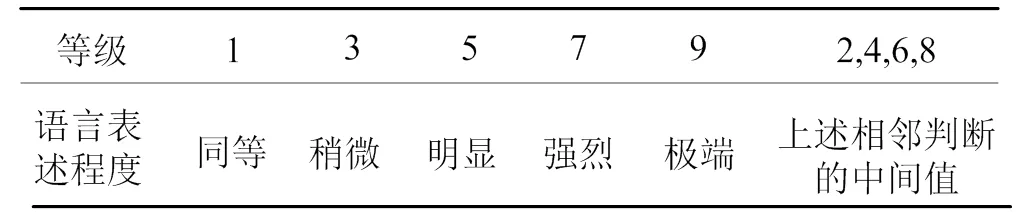
2) 给出判断矩阵，然后对指标进行权重排序和一致性检验。权重排序采用特征值法求取。

具体求解步骤为：

①根据标度原理，构造两两比较矩阵

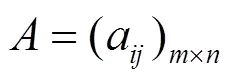
②将判断矩阵A的各列作归一化处理，即

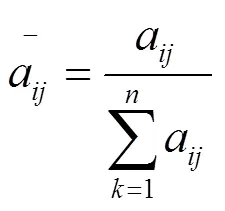
③求出判断矩阵A每一行各元素之和，即：

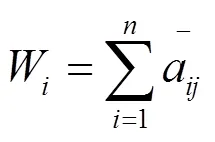
④对W进行归一化处理，即：

⑤进行一致性检验

一致性检验是针对判断矩阵是人们主观判断而得，不可避免有估计误差而进行的。对判断矩阵进行一致性检验分为次序一致性检验和基本一致性检验。次序一致性是检验判断矩阵内元素，a>1，a>1能否导出a>1，若能则满足次序一致k性，否则不满足。基本一致性是检验一致性比例CR是否小于0.1，若小于则满足基本一致性要求，否则不满足。

判断矩阵的次序一致性和基本满意一致性之间没有必然的联系：具有次序一致性的判断矩阵不一定具有基本满意一致性；而具有基本满意一致性的判断矩阵又不一定具有次序一致性。其中次序一致性是判断矩阵可用的基本条件，违反次序一致性的判断反映了决策者对问题缺乏起码的深思熟虑，而由不具备次序一致性的判断矩阵导出的权值不可能是对某种属性合理的测度。因此，对决策者给出的判断矩阵，首先应该检查其是否具有次序一致性，然后再检查其是否具有基本满意一致性[2]。

次序一致性的检验采用文献[3]中的检验步骤。基本一致性的步骤如下：

①根据权重排序方法计算判断矩阵的最大特征值λ。

②计算一致性指标CI

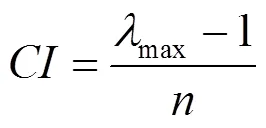
表2 1~7阶矩阵的RI值

2.2 模糊综合评判

船舶电力推进系统仿真可信性评价指标体系中，有的指标类型为定性的，如评价体系中子指标：系统仿真模型、数据有效性，不能采用定量的方法进行分析。因此，需要根据专家知识，利用模糊综合评判法对系统进行定性分析[4-7]。模糊综合评判的基本步骤为：

1）针对影响船舶电力推进系统仿真可信性的指标因素，建立因素集：

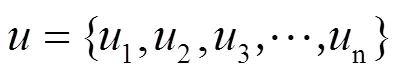
2）根据所确定的因素集，建立相应的评价标准，即评判集：

4）模糊综合评判：

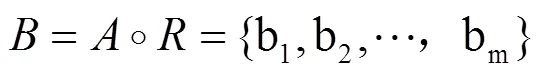
2.3 相似度原理

相似度[8]是为衡量系统间相似程度的大小所进行的量化，适用于定量指标的判断分析。

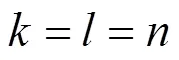
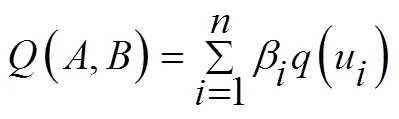
各个子系统的相似元计算公式为：

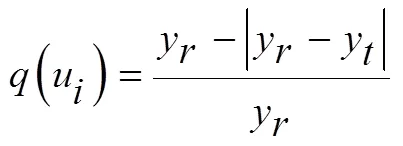
2.3.1数据预处理

对于船舶电力推进系统仿真进行可信性分析时，评价体系中的子指标系统仿真结果，其仿真数据与实际系统数据均可得到，故可采用相似度原理分析。

对于系统仿真所得的结果，指标类型不同，其所得数据类型也不同。有的指标数据越小其相似度越高，有的则是数据越大相似度越高。因此，对系统仿真结果进行可信性分析时，首先需要通过线性变换方法对原始数据进行归一化处理。

①当指标值越大时系统仿真结果越好，即指标类型为效益型。数据预处理公式：

Y=(X-min)/(max-min) (10)

②当指标值越小时系统仿真结果越好，即指标类型为成本型，数据预处理公式：

Y=(max-X)/(max-min) (11)

式中：X为系统仿真结果所得的值，Max(或Min)为对同一指标而言船舶电力推进系统可能出现或期望的最大值(或最小值)。

2.3.2相似度隶属函数的求取

对船舶电力推进系统仿真进行可信性分析时，评价方法中既包含有定性方法也包含有定量方法。本文通过采用自适应神经网络模糊推理系统ANFIS来建立模糊模型，将系统所得的相似度转化为与模糊综合评判一致的模糊向量[9]。

自适应神经网络模糊推理系统是通过训练样本来训练网络，并获取系统初始隶属函数，最终利用反向传播算法来修正初始隶属函数，求取最终系统的隶属函数。而通常系统隶属函数的确定是通过专家直接给出或者依据经验数据而得，所得到的隶属函数并非能完全反应真实系统，隶属函数中各节点的数据如果选取不恰当，会对系统的模糊判断带来误导[10]。

较之于凭主观经验设定的系统隶属函数，自适应神经网络模糊推理系统能够更好的反映系统特点，并能依据系统特点反向传播对隶属函数进行修正，直到误差达到一定范围终止。

对于子指标B系统仿真结果而言，可以依据系统在工况C3、C4、C5、C6的仿真数据与实际数据求取各工况与实际相比的相似度，并依据不同工况相对于系统仿真结果的权重大小求取子指标B的相似度。通过数次仿真获取不同子系统的相似度，并选取数组训练样本和测试样本。设定C3、C4、C5、C6指标的相似度为输入集，B指标的相似度为输出集，并利用反向传播算法来修正并确定隶属函数。

3 实际算例

3.1 系统各指标权重的确定

对于船舶电力推进系统仿真可信性分析评价体系中各指标权重的计算，采用层次分析法原理，通过专家打分获取判断矩阵，然后利用特征根法计算权重向量并进行次序一致性和基本一致性检验。若不满足要求，要求专家对判断矩阵进行重新修正，直到满足一致性要求为止。鉴于篇幅原因，本文只给出权重结果。其中WA为B1、B2、B3相对于A的权重向量。WB1、WB2、WB3为指标B1、B2、B3下层指标相对于上层指标的权重。

WA= {0.4286, 0.1429, 0.4286}.

WB1= {0.5, 0.5}.

WB2= {0.25, 0.25, 0.25, 0.25}.

WB3= {0.0579, 0.2002, 0.3710, 0.3710}.

3.2 模糊综合评判

针对指标B1和B3的类型均为定性指标，采用专家打分的方式进行评判分析。通常，人们对指标的评价常用满意程度来表示，因此，划分评判集时可以通过满意程度来划分。但评判集划分并非越多越好，越多则需要更多的模糊控制规则。为此，对于指标B1和B3而言，将其评判划分为4级，分别为{好、较好、较差、差}，即V={好、较好、较差、差}。专家在打分时相应的判断依据如表3：

表3 专家判断依据

设U={U1、U2、U3}，U1、U2、U3分别表示系统仿真模型、系统仿真结果、数据有效性三个指标。则相应的子指标可以表示为:U1={U11、U12}，U2={U21、U22、U23、U24}，U3={U31、U32、U33、U34}。通过专家对指标U1、U3的评判及统计分析，得到如下模糊判断矩阵。

3.3 系统相似度

根据系统仿真在启航、倒车、停车及突变负载工况下的数据以及实际系统在对应工况下的相应数据，求取各指标的相似度。

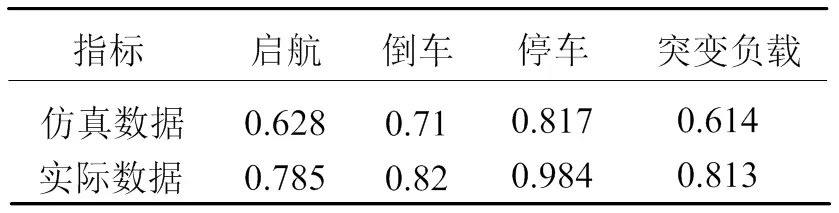
对于指标B2而言，系统仿真数据与实际系统数据可以通过实验或测量而得。对于船舶电力推进系统而言，随机选取一组仿真系统在不同工况下的数据，并与相同工况下的实际数据进行比较。其中数据见表4。

利用式（9）、(10)、(11)求取C3、C4、C5、C6的相似度：

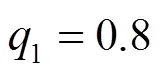
利用层次分析法所得C3、C4、C5、C6相对于B2的权重向量，根据式(7)、(8)求取指标B2的相似度，得：

=0.25*0.8+0.25*0.87+0.25*0.83+0.25*0.76

=0.815

表4 仿真数据与实际系统相应数据

为了将仿真所得结果模糊化，确定仿真结果的隶属函数，通过对系统进行多次仿真并随机选取20组数据作为训练样本，5组数据作为测试样本，网络训练200次，隶属函数类型设为高斯型，隶属度个数与模糊综合评判划分个数相同，为4个。并利用反向传播算法来修正初始隶属函数。最终所得的初始隶属函数和训练后的隶属函数如图2。训练过程中样本集和测试集的均方根误差变化情况如图3。由图3中两条误差曲线的变化情况可知，模糊系统的设计与数据是匹配的，满足要求。

通过查询训练后所得的模糊隶属函数曲线，如图2所示，将上述求得的相似度转化为模糊向量，得：

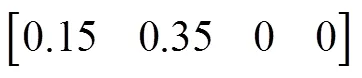
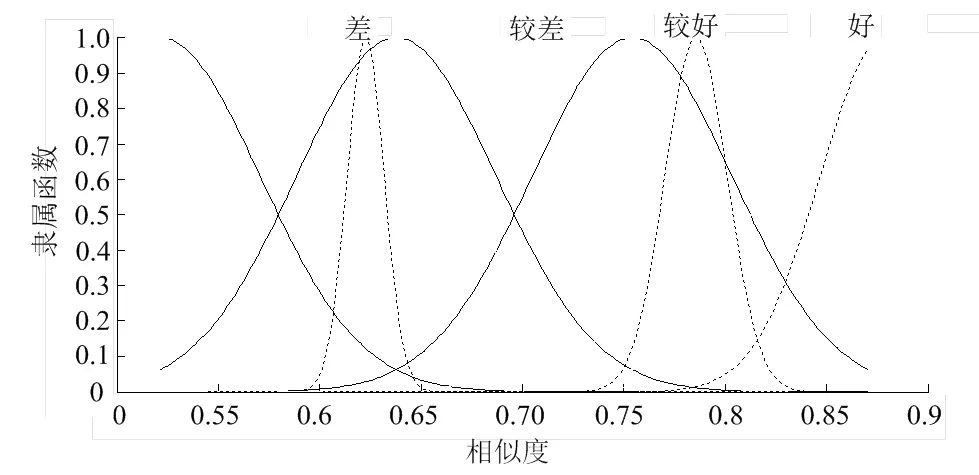
图2 初始和训练后的隶属函数

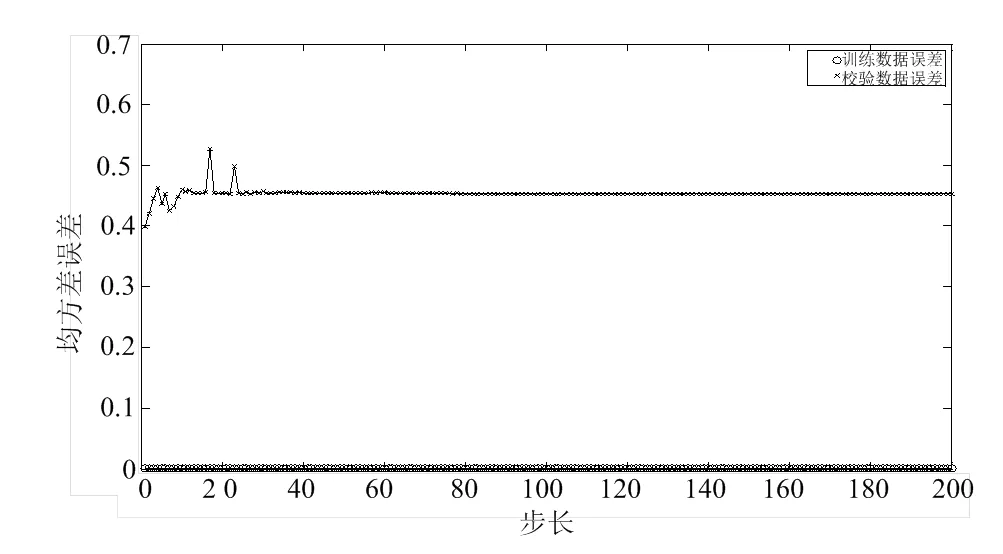
图3 训练过程中均方根误差的变化曲线

3.4 系统仿真可信度计算

针对B1、B2、B3模型，利用模糊评判原理进行二级模糊综合评判。得到B1、B3的一级模糊评判矩阵为:

B1= WB1*R1

= [0.45 0.3 0.15 0.1]

同理得B3一级模糊评判矩阵为：

B3= [0.3088 0.3113 0.2629 0.1171]

以 B1、B2、B3为元素，构造单因素模糊向量，进行二次模糊评判，得：

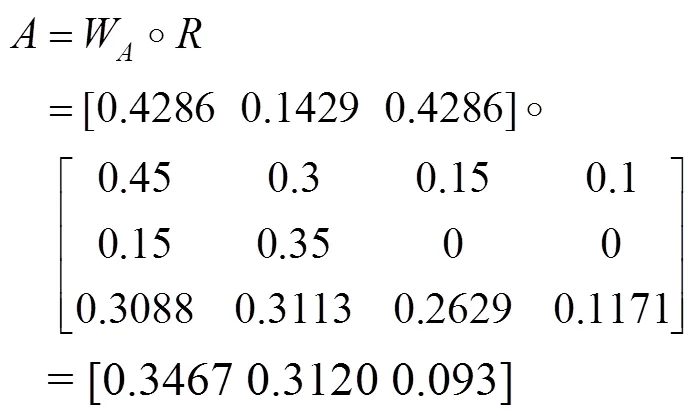
由上述计算结果可知其最大隶属度为0.3467。根据最大隶属度原则，最大隶属度对应于模糊评语的“好”。因此可以得到该船舶电力推进系统仿真的可信性为“好”。

4 结论

本文通过结合相似度原理和模糊综合评判两种定性与定量的方法，对船舶电力推进系统仿真进行可信性分析。首先建立船舶电力推进系统仿真可信性分析评价指标体系，并利用层次分析法原理确定各指标的权重大小；然后针对各指标特点采用相应的方法进行分析计算，利用自适应神经网络模糊控制系统对定量方法所得结果进行模糊化；通过模糊综合评判确定系统最终的可信度。

该方法能够更好地解决船舶电力推进系统中不同指标类型的特点，可以较为客观、综合、全面的分析船舶电力推进系统的仿真可信度。同时该方法对定量方法所得结果进行模糊化时，有效地避免了通过专家经验或历史数据确定隶属函数所带来的不确定性，真实的反应了系统特点。该方法理论清晰，便于操作，且工作量不大，可以较好的应用于实际系统。

[1] 徐树柏. 层次分析法[M]. 天津大学出版社,1988.

[2] 朱建军. 层次分析法的若干问题研究及应用[D]. 东北大学博士论文, 2005.

[3] 朱建军, 王梦光, 刘士新. AHP判断矩阵一致性改进的若干问题研究[J]. 系统工程理论与实践. 2007. 1:18-22.

[4] 杨军. 基于模糊理论的卫星导航系统综合效能评估研究[J]. 宇航学报. 2004, 25(2): 147-151.

[5] 岳韶华, 周国安, 王颖龙. 地面防空作战效能的模糊综合评价[J]. 系统工程与电子技术. 2001. 3(9): 67-69.

[6] 肖峻, 王成山, 周敏. 基于区间层次分析法的城市电网规划综合评判决策[J]. 中国电机工程学报. 2004, 24(4): 50-57.

[7] 朱宗林, 郭世民. 自动控制装置系统综合评估研究[J]. 自动化学报, 1999, 25(2): 199-203.

[8] 徐迪. 基于相似理论的系统仿真可信性分析[J]. 系统工程理论与实践, 2001(4): 49-52.

[9] 吴晓莉, 林哲辉等. MATLAB辅助模糊系统设计[M]. 西安电子科技大学出版社, 2002.

[10] 王石青, 邱林, 王志良等. 确定隶属函数的统计分析法[J]. 华北水利水电学院学报, 2002. 23(1): 68-71.

Research on the Credibility of the Ship Electric Propulsion Simulation System Based on the Comprehensive Evaluation

Liu Jianbo

(Naval Representatives Office in Jiangnan Delta Refco Group Ltd, Shanghai 201913, China)

U664.14

A

1003-4862（2013）04-0008-05

2012-11-15

刘建波（1970－），男。专业方向：舰船电力推进。