疏松砂岩油藏水平井管外地层塑性挤压充填模拟

贾锁刚，董长银，武 龙，隆佳佳，冯胜利，陈 君，阿雪庆

(1.中国石油青海油田分公司钻采院，甘肃敦煌736200;2.中国石油大学石油工程学院，山东青岛266580;3.川庆钻探工程有限公司钻采工程技术研究院长庆分院，陕西西安710018)

水平井砾石充填包括管外地层砾石充填和套管内循环砾石充填，是一种效果好、有效期长的防砂(完井)工艺。管外砾石充填是指高压大排量条件下砾石颗粒由携砂液带入地层，在管外地层中形成高渗透带。管外砾石充填技术不但具有良好的防砂效果，而且还可以最大程度降低对油气井产能的伤害，甚至具有增产作用［1-3］。以上优点使水平井管外砾石充填成为疏松砂岩水平井砾石充填防砂完井的发展方向之一，并已有少量实际应用。文献［4］中提出了疏松砂岩地层水平井管外砾石充填的两种模式:裂缝开裂延伸和塑性挤压破坏模式，并研究了管外地层岩石破坏模式的判别方法。对于水平井地层岩石的破坏研究，重点主要集中在低渗透水平井水力压裂领域的裂缝开裂条件和裂缝延伸领域［5］，对疏松砂岩地层在高压挤注条件下的塑性挤压充填模拟研究几乎处于空白。文献［6］根据摩尔－库仑准则和平面应变轴对称问题的基本方程，建立了垂直井近井地带塑性变形区的应力与应变关系数学模型。文献［7］依据离散元理论，使用商业模拟软件PFC2D对地层岩石按照胶结强度强、胶结强度中等、胶结强度弱等3种情况进行模拟，得到一些定性认识。但上述研究均未对水平井开展针对性研究，也未形成系统的模拟理论与方法。笔者针对上述水平井管外地层砾石充填问题，基于沿水平井井身轨迹变化的主应力及地层岩石力学参数非均质分布的基础，建立疏松砂岩地层高压挤注条件下的水平井管外地层塑性挤压充填模拟数学模型，预测充填半径随施工时间的变化及其沿水平井井身轨迹的分布规律。

1 水平井近井地应力分布

1.1 水平井近井地应力

假设:在地层深处，高压挤压井段围压起主要作用，并且井筒直径远小于施工井段长度，不考虑井眼轴线方向的应变。

基于上述假设，疏松砂岩地层水平井管外地层塑性挤压充填可简化为垂直于井筒轴线的平面应变问题。使用柱坐标系，以具有普遍意义的斜井为研究对象，原始地层主应力可分解为斜井直角坐标系下的 σxx、σxy、σyy、σyz、σzz和 σxz6 个应力分量。由于坐标转换后井周截面上的最大和最小主应力不一定是σxx和σyy，因此，为了得到井周截面上的最大和最小主应力，仍需将坐标系绕z轴逆时针旋转(图1)。在绕井眼轴线旋转过程中，各个面上的应力将发生变化。根据旋转变换矩阵可得到各个面上转换后的应力分量 σxx′、σyy′、σzz′、σxy′、σxz′和 σyz′。上述转换是为了保证得到一个最大应力σxx′和对应的最小应力 σyy′。

应力转换关系［8］表达式为

其中绕z轴旋转的变化矩阵为

转换坐标后的应力分量可表示为

式中，σxx、σyy、σzz和 σxx′、σyy′、σzz′分别为坐标系转换前、后的主应力，MPa;σxy、σyz、σzx和 σxy′、σxz′、σyz′分别为坐标转换前、后的剪切应力，MPa;γ为绕井眼轴线z逆时针旋转的角度，rad。

图1 坐标系旋转示意图Fig.1 Sketch map of coordinate system transformation around z axis

在绕井眼轴线z逆时针旋转的角度γ从0增加到π的过程中，会出现一个最大的主应力σxx′和对应的最小主应力σyy′。研究表明，3个剪切应力相对于主应力值小一个数量级，计算时忽略剪切应力的作用，即认为岩石受力变形后其应力分布仍保持在垂直井筒轴线的平面上，且井筒截面上应力σxx和σyy的差值要比应力值小一个数量级。所以，可认为井筒受均匀压应力 σ(R)=(σxx′+σyy′)/2 的作用，建立数学模型可得到沿井周的破坏半径。

1.2 挤压条件下水平井近井破坏带划分

假设:①水平井裸眼井段井眼轴线为直线，无井筒迂曲;②较短的井眼长度单元情况下地应力沿井轴方向无变化，只随角度和半径变化;③近井地带岩石各向同性;④剪应力数量级比正应力小，可忽略;⑤近井地层围岩受均匀压应力作用;⑥破坏模式为塑性挤压充填。

如图2所示，将近井地层分为井筒、中间塑性压实区和远处弹性变形区。对水平井实施高压挤压充填作业时，水平井筒内压力为pd。开始充填时，携砂液对井筒周围岩石进行挤压充填，岩石发生变形。如图2所示的充填压实过程中水平井筒半径由r0增大为r1，在塑性压实区域半径r2以外的地层岩石仍保持原始弹性变形状态。

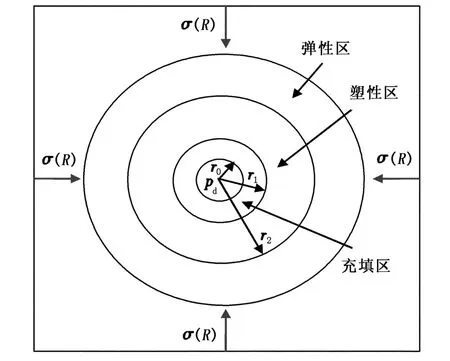
图2 水平井近井挤压充填带划分示意图Fig.2 Sketch map of compaction packing zone divide around horizontal well bore

2 水平井管外地层塑性挤压充填模型

2.1 弹性变形区的应力与位移

采用柱坐标系，对于给定的深度h，由r、θ确定空间上一点。任意点(r、θ)处的岩石应变张量的几何方程［8］为

式中，εz、εr和εθ分别为轴向应变、径向应变和切向应变;u为岩石单位径向位移，m;w为岩石单位轴向位移，m。

根据广义胡克定律可以得到岩石变形的本构方程为

其中

式中，σr、σθ和σz分别为径向、切向和垂向主应力，MPa;υ为泊松比;E为弹性模量，MPa。

根据假设条件，轴向应力变化和剪切应力可以忽略，则垂直于井筒轴线的截面为平面应变，变形后仍保持为平面。这样岩石的应力平衡方程式可简化为

联立可得

采用分离变量法求解得到方程(7)的通解为

式中，c1和c2为积分常数。

对于弹性区，边界条件为

式中，R为外边界半径，m;r2为塑性压实区最大半径，m。

求解可得

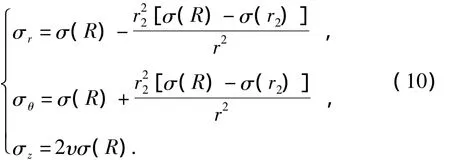
弹性区相对位移为

根据式(11)可得弹塑性交界处(r=r2)的相对位移为

2.2 塑性变形区域的应力与位移

在水平井靠近井筒的塑性变形区域内，地层岩石突破弹性变形条件，产生塑性破坏，其应力－应变关系遵从Mohr-Coulun准则，可表示为

式中，σ1为最大主应力，MPa;σ3为最小主应力，MPa;C为岩石内聚强度，MPa;φ为岩石内摩擦角，rad。

在弹性变形阶段，井筒内边界处的径向及切向应力表示为

对于水平井管外地层塑性挤压充填，井内压力较高，一般有pd＞σ(R)。此时 σθ＜σr，径向应力 σr表现为压应力，切向应力σθ表现为拉应力，水平井眼直径扩大，即有σ3=σθ和σ1=σr。根据方程(13)有

将式(15)带入平衡方程(6)，得

在充填区与塑性区交界处，即r=r1处σr=pd，由此可得

将式(17)带入式(16)得

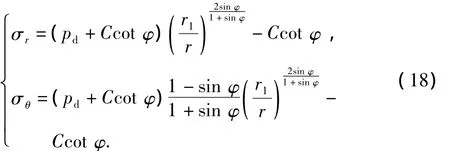
在弹性区和塑性区交界处，即r=r2处有

由式(15)和边界条件式(19)可得

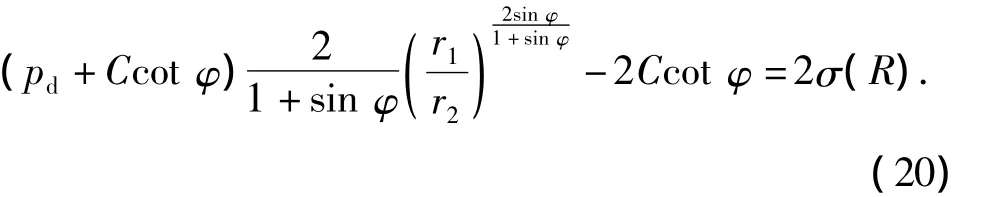
化简可得到塑性区扩张比为

式中，r1为裸眼塑性扩张半径，m。

2.3 管外地层挤压充填区和压实带半径计算

根据水平井塑性挤压段的岩石体积变化等于弹性变形区的体积变化与塑性压实带的体积变化之和的原理，可得

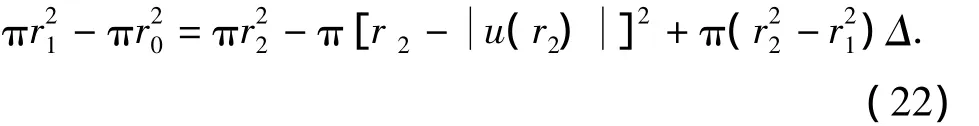
式中，Δ为塑性压实带的平均体积应变;r0为水平井筒半径，m。

疏松砂岩油藏岩石由岩石骨架颗粒和孔隙空间组成，且颗粒间胶结疏松。在进行高压挤压充填作业时，随着泵压增高，井底压力增大，地层岩石介质所承载的内部应力也不断升高，岩石基质颗粒间发生崩塌和聚结。挤压充填过程中，水平井筒周围地层岩石介质颗粒之间的原始胶结被破坏，颗粒间隙变小，岩石孔隙度也变小。根据上述分析，塑性变形区的体积应变可按疏松砂岩施工前后的岩石介质孔隙度的比值计算:

式中，φ1为疏松砂岩地层岩石的原始孔隙度，即施工前的地层孔隙度;φ2为高压挤压塑性压实区的岩石介质孔隙度。

对方程(22)进行简化并忽略［u(r2)］2项可得

在高压挤压作业中水平井井底施工压力高于压应力，即pd＞σ(R)。因此根据计算得到的弹性变形区位移方程(21)可以推导得到

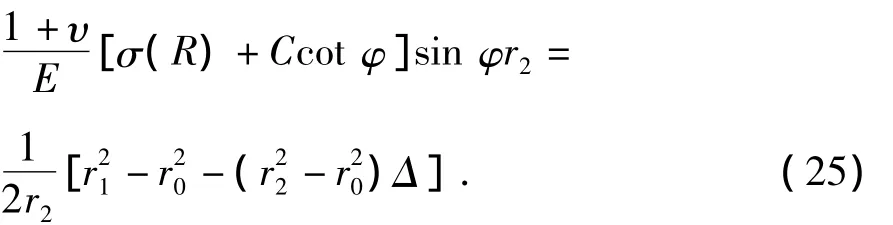
由式(25)可得井径扩张率为

方程(26)可用来计算塑性变形带的扩张率，从而进一步得到井径扩张率r1/r0，最后可求出塑性挤压充填带的半径r1和塑性压实带半径r2。

3 模拟计算结果分析

某水平井井斜角88.63°，垂深1.18382 km，井斜方位角248.5°。最大原始水平主应力方位角120°，利用测井计算得到的平均地层岩石密度2002.3 kg/m3，最大水平应力构造系数0.902，最小水平应力构造系数0.257。已知该井2.1～2.2 km井段的测井数据，并根据其计算得到岩石力学参数沿井身轨迹的分布规律。

3.1 管外挤压充填破坏剖面的动态模拟结果

利用本文模型对该算例水平井水平段管外塑性挤压破坏剖面进行动态模拟。不同井底压力下的充填形态如图3所示。

根据图3的模拟结果可知，由于水平段较长，导致岩石力学参数及地应力的非均质性，管外地层塑性挤压充填也表现出较强的非均匀性，其充填剖面的分布规律与岩石强度参数的分布规律相似。对比分析结果表明，岩石强度相对较低的井段，最终挤压破坏的半径相对较大。算例中，在该井后半段岩石强度相对较高，模拟计算得到的挤压充填破坏半径也相对较小。

图3 水平井管外地层破坏剖面动态模拟Fig.3 Dynamic simulation of failure radius distribution along horizontal wellbore

当井底施工压力较低时，水平段管外塑性挤压破坏形态相对比较均匀，充填破坏半径沿井身轨迹的变化差异不十分明显。当井底施工压力达到较高值时，水平段管外塑性挤压破坏形态及尺寸逐渐沿井身轨迹方向呈现出一定的非均匀性。

3.2 水平井挤压充填横向破坏形态静态模拟结果

使用上述算例水平井井身2.15 km处的岩石力学数据进行管外塑性挤压充填破坏形态的模拟计算与分析。该位置处地层岩石的内摩擦角为39.1°，岩石内聚力为3.85 MPa，泊松比为0.314，岩石弹性模量为11952 MPa。不同井底压力下的管外破坏形态如图4所示。

由图4可以看出:当井底施工压力较低时，水平井管外地层塑性挤压破坏形态相对比较均匀，其沿井周角的非均质性不十分明显;而当井底施工压力逐步达到较高值后，管外地层岩石的塑性挤压破坏形态也表现出一定的非均匀性。这表明，疏松砂岩油气藏水平井在高压挤注情况下，近井地带地层岩石主要受井眼内流体压力的影响较大，而受外围地层地应力的影响相对较小。但随着管外地层塑性挤压破坏半径的增加，外围地层地应力的作用和影响逐渐体现出来，表现为横向塑性挤压剖面的非均匀性。

图4 水平井管外地层径向破坏剖面动态模拟Fig.4 Dynamic simulation of failure radius around horizontal wellbore

3.3 挤压充填扩张比敏感性分析

3.3.1 岩石内摩擦角对充填结果的影响

设定如下计算参数:内聚力2.0 MPa，弹性模量800 MPa，岩石泊松比0.3，体积应变0.1，平均井筒截面压应力σ(R)=20 MPa。不同疏松砂岩内摩擦角条件下，高压挤压过程中，井径扩张率r1/r0及压实区扩张率r2/r1随井底压力pwf变化曲线如图5所示。

在内摩擦角相同的情况下，井径扩张率r1/r0随井底压力的增大而增大。在井底压力略高于井筒截面压应力时井径扩张率r1/r0接近于1，说明较低的井底压力不会引起较大的井径扩张，但其增大速率随着井底压力的升高有加大的趋势。在井底压力相同的情况下，内摩擦角减小会导致井径扩张率r1/r0增大。内摩擦角数值越小，井径扩张率r1/r0增加的幅度越大;反之，增大幅度越小。

在内摩擦角相同的情况下，井底压力越高，塑性压实区域扩张率r2/r1越高，两者成正比关系。当井底压力相同时，内摩擦角越小，塑性压实区扩张率r2/r1越大。当内摩擦角数值较小时，塑性压实区的扩张率r2/r1增幅随井底压力的增大而增大。

3.3.2 内聚力的影响

取疏松砂岩的内摩擦角 20°，弹性模量 800 MPa，泊松比0.3，体积应变取0.1，平均井筒截面压应力σ(R)=20 MPa。不同疏松砂岩内聚力条件下，高压挤压过程中，井径扩张率r1/r0以及压实区扩张率r2/r1随井底压力的变化如图6所示。

由图6可以看出:在井底压力较低的情况下，内聚力对井径扩张率及压实区扩张率影响较小;在较高井底压力下，随内聚力减小，内聚力对井径扩张率及压实区扩张率的影响增大。当内聚力较低时，井底压力增加到一定程度后，较小的压力变化就可以引起较大的井径扩张率变化;当内聚力较高时，井径扩张率随井底压力的变化较小。

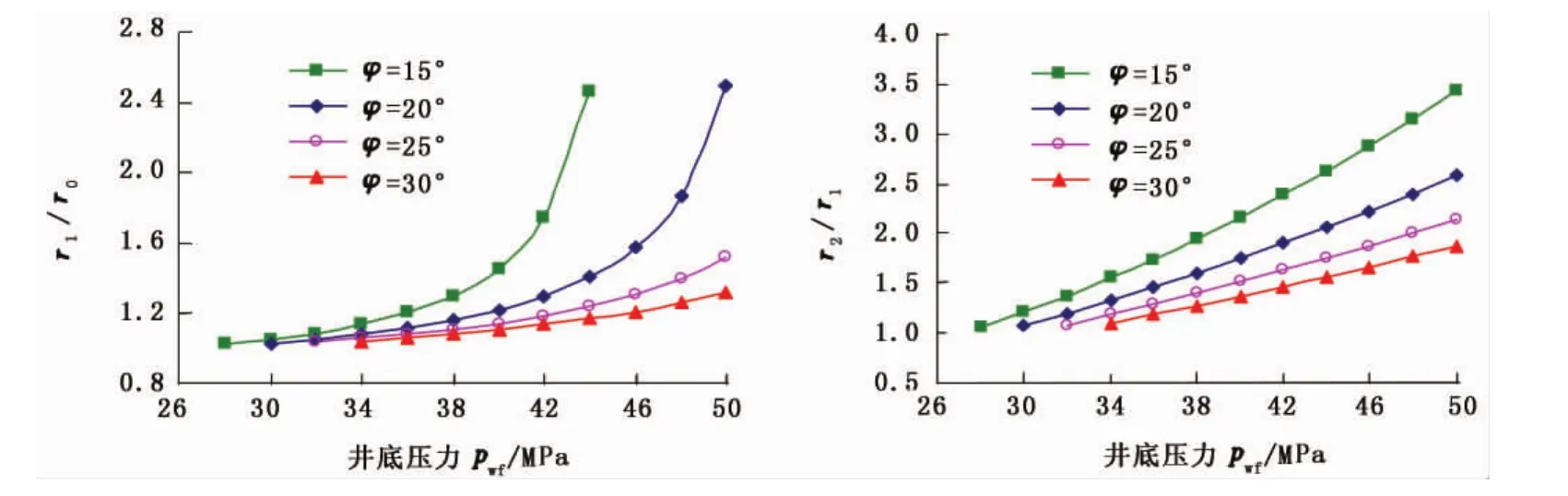
图5 内摩擦角对充填扩张率的影响Fig.5 Influence of rock internal friction angel on extension ratio of packing

图6 内聚力对充填扩张率的的影响Fig.6 Influence of cohesive strength on extension ratio of packing

3.3.3 弹性模量的影响

取疏松砂岩的内摩擦角20°，内聚力2 MPa，泊松比0.3，体积应变0.1，平均井筒截面压应力 σ(R)=20 MPa。图7为水平井高压挤压过程中不同弹性模量条件下的井径扩张率r1/r0随井底施工压力的变化关系曲线。

图7 弹性模量对井径扩张率的影响Fig.7 Influence of elastic modulus on extension ratio of borehole radius

由图7可看出，在压力较低的情况下弹性模量对井径扩张率影响较小。随井底压力升高，弹性模量对井径扩张率影响变大。在较高的井底压力下较小的压力变化就可以引起较大的井径扩张率变化。

3.3.4 泊松比的影响

取疏松砂岩的内摩擦角20°，内聚力2 MPa，弹性模量800 MPa，体积应变0.1，平均井筒截面压应力 σ(R)=20 MPa。

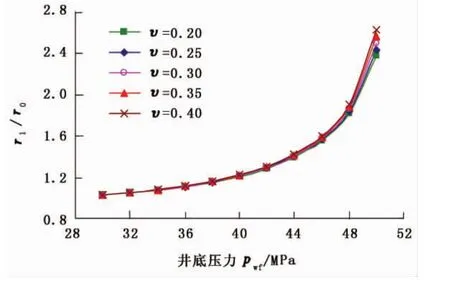
图8 泊松比对井径扩张率的影响Fig.8 Influence of Poisson ratio on extension ratio of borehole radius

图8为水平井高压挤压过程中不同泊松比下的井径扩张率r1/r0随井底施工压力的变化曲线。由图8可看出，在低井底压力情况下曲线基本重合，在较高的井底压力下各曲线差异也很小，说明泊松比对充填扩张率的影响非常小，可忽略不计。

4 结论

(1)由于沿水平井井身轨迹岩石力学参数及地应力的非均质性，管外地层塑性挤压充填剖面也表现出较强的非均匀性，并与岩石参数分布规律相关。岩石强度相对较低的井段，最终挤压破坏的半径相对较大。当井底压力较低时，水平段管外塑性挤压破坏形态沿井身轨迹的变化不明显;当井底压力较高时，挤压破坏形态非均质性逐步变得明显。

(2)随井底压力增高，充填扩张率对各影响因素的敏感性急剧增加。疏松砂岩岩石内摩擦角、内聚力、弹性模量随着井底压力的增加对充填扩张率影响增大。泊松比的影响最小，可以忽略。

［1］ 董长银.油气井防砂技术［M］.北京:中国石化出版社，2009:48-60.

［2］ 董长银，张琪.水平井砾石充填过程实时数值模拟研究［J］.石油学报，2004，25(6):96-100.

DONG Chang-yin，ZHANG Qi.Real-time numerical simulation of gravel-packing process in horizontal wells［J］.Acta Petrolei Sinica，2004，25(6):96-100.

［3］ 李明忠，李彦超，王卫阳，等.考虑井筒变质量流动的砾石充填水平井产能预测［J］.中国石油大学学报:自然科学版，2011，35(3):89-93.

LI Ming-zhong，LI Yan-chao，WANG Wei-yang，et al.Productivity prediction for gravel-packed horizontal well sonsidering variable mass flow in wellbore［J］.Journal of China University of Petroleum(Edition of Natural Science)，2011，35(3):89-93.

［4］ 董长银，刘春苗，武龙，等.高压挤注条件下水平井管外地层破坏模式及其判别方法［J］.中国石油大学学报:自然科学版，2012，36(5):45-49.

DONG Chang-yin，LIU Chun-miao，WU Long，et al.Formation rock failure mode and its recognition method under high pressure squeezing condition in horizontal wells［J］.Journal of China University of Petroleum(Edition of Natural Science)，2012，36(5):45-49.

［5］ 陈勉，陈治喜，黄荣樽.大斜度井水压裂缝起裂研究［J］.石油大学学报:自然科学版，1995，19(2):30-35.

CHEN Mian，CHEN Zhi-xi，HUANG Rong-zun.Hydraulic fracturing of highly deviated wells［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，1995，19(2):30-35.

［6］ 闫相祯，王伟章，杨秀娟，等.近井地带高压挤压问题的解析［J］.中国石油大学学报:自然科学版，2008，32(3):103-107.

YAN Xiang-zhen，WANG Wei-zhang，YANG Xiu-juan，et al.Analytical solution of high-pressure squeezing problems at stratum near well［J］.Journal of China University of Petroleum(Edition of Natural Science)，2008，32(3):103-107.

［7］ 王伟章，闫相祯.高压挤压防砂充填带形态仿真模拟［J］.潍坊学院学报，2009，9(2):1-5.

WANG Wei-zhang，YAN Xiang-zhen.Numerical simulation of packing zone morphology with high pressure gravelpacking sand-prevention technology in unconsolidated sandstone［J］.Journal of Weifang University，2009，9(2):1-5.

［8］ 闫铁，李士斌.深部井眼岩石力学理论与实践［M］.北京:石油工业出版社，2002:11-33.