基于正交试验的风电机组塔架结构参数的优化设计

顾岳飞

（上海电气风电设备有限公司，上海 200241）

0 引 言

风电机组塔架受到多种载荷的共同作用，主要有塔架顶部受到的惯性力、重力载荷、风轮承受的空气动力载荷、自然风的作用载荷和风电机组起停时冲击载荷，海上机组还受到波浪载荷。基于塔架的特点及性能要求，在对塔架进行结构设计时，必须进行塔架的静强度分析、模态分析[1]、稳定性分析[2]和疲劳分析[3]。

塔架的结构由多种因素决定，不可能做大量的试验来研究。通过有限元分析方法研究[4]，可以弥补试验数据的不足，可设计大量不同形式、不同尺寸的塔架，来分析各种可能因素对塔架结构的影响，因此有较高的实用价值和参考价值。运用正交试验方法设计[5]和多元线性回归分析，建立优化数学模型，再应用MATLAB优化工具箱对模型进行求解，得到了塔架结构优化结果。

1 正交试验设计

1.1 试验指标和设计参数

按照塔架的结构设计要求，需要进行静强度分析、模态分析、稳定性分析和疲劳分析。因此，选取极限强度最大应力、模态一阶频率、屈曲安全系数和疲劳损伤值为正交试验的试验指标。

影响塔架结构设计的因素比较多，本文主要考虑塔底外径、塔顶外径、门段壁厚、底部壁厚和顶部壁厚5个因素。如图1所示。

表1 正交试验因素水平表

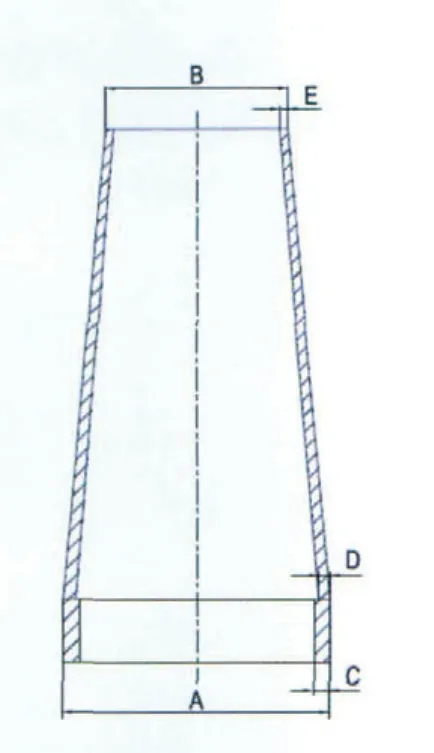
图1 塔架结构图

为了便于衡量各因素对试验指标的影响，在这里选取最初的设计尺寸作为基本尺寸，各尺寸以基本尺寸为基准上下变动，同数量及尺寸变化幅度大致相等。初步将试验水平定为3，可以获得正交试验因素水平表，如表1所示，单位：mm。

1.2 正交试验设计方案

正交试验的试验样本的选取不是随机的，而是按照正交表来选取和安排试验，使试验中每一因素的不同水平的试验次数相同，且和不同因素的各水平相遇几率相等。这种方案能够比较全面地反映各因素各水平对试验指标的影响程度。因此，可以利用较少的试验次数得到较为精确的试验结果[6]。

根据表1建立L18（3^5）正交表，L为正交表代号，试验次数为18次，观察5个因素，每个因数为3水平，其试验方案的正交表如表2所示。

根据正交表确定每号试验的方案，然后进行试验，得到以试验指标形式表示的试验结果。试验的过程是使用有限元法，建立18组试验号的模型，对每一组试验号进行有限元计算，得到其试验指标。

2 参数优化设计

优化设计是20世纪60年代初发展起来的一门学科，它是将最优化原理和计算技术应用于设计领域[7]，为工程设计提供一种重要的科学设计方法。利用这种新的设计方法，就可以从众多的设计方案中寻找出最佳设计方案，从而大大提高设计效率和质量。

表2 试验方案正交表

2.1 试验分析数据

根据正交试验的结果，建立线性回归分析数据表，如表3所示。数据主要包括在不同试验组合下的极限最大应力、模态一阶频率、屈曲安全系数和疲劳损伤值。为了获得更有用的信息，需要对其进行进一步的分析和处理。数据分析主要是运用数理统计分析方法对数据进行多元线性回归分析，得到试验指标与设计变量之间的回归方程式，为优化提供约束条件。

表3中X1～X5是塔架试验因素，也是线性回归分析的设计变量，依次为塔底外径、塔顶外径、门段壁厚、底部壁厚和顶部壁厚，f是塔架一阶频率，σ是极限最大应力，S1是疲劳损伤值，S2是屈曲安全系数，G是根据Solidworks三维设计软件计算得到的塔架质量。

2.2 回归分析

线性回归是利用数理统计中的回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用十分广泛。本文运用数据统计分析软件SPSS18.0[8]对这些目标量进行多元线性回归分析，分别得出f、σ、S1、S2和G与设计变量X1～X5之间的函数关系式。

对塔架一阶频率f进行回归分析，回归分析结果如表4和表5所示。

表4为方差分析表，该表可以用来检验回归分析的显著性。表中列出了回归项和残差项的平方和、自由度、均方、统计值和显著性水平。由于显著性水平小于0.05，所以可以认为所建立的回归方程式有效。

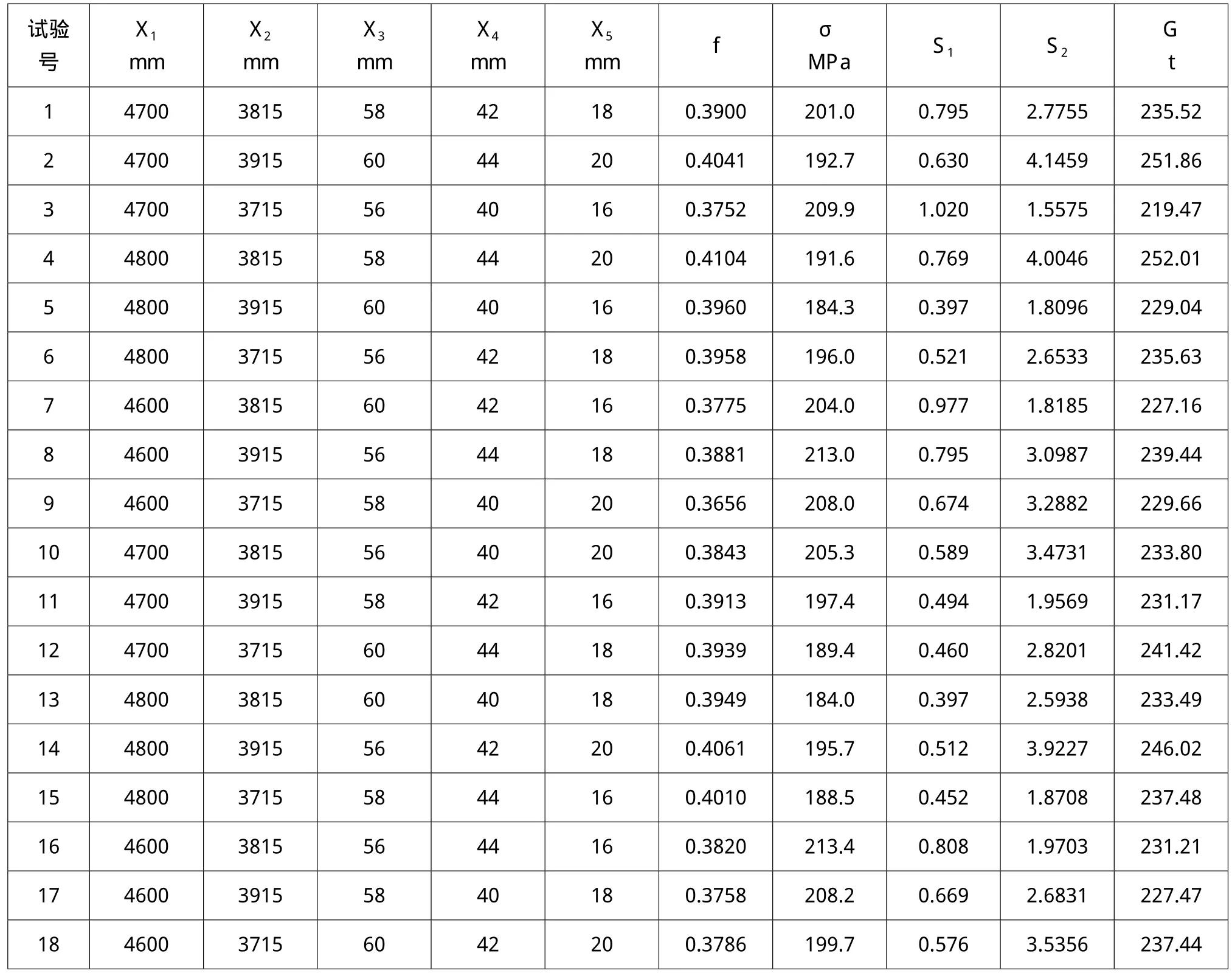
表3 线性回归分析数据表

表4 方差分析表

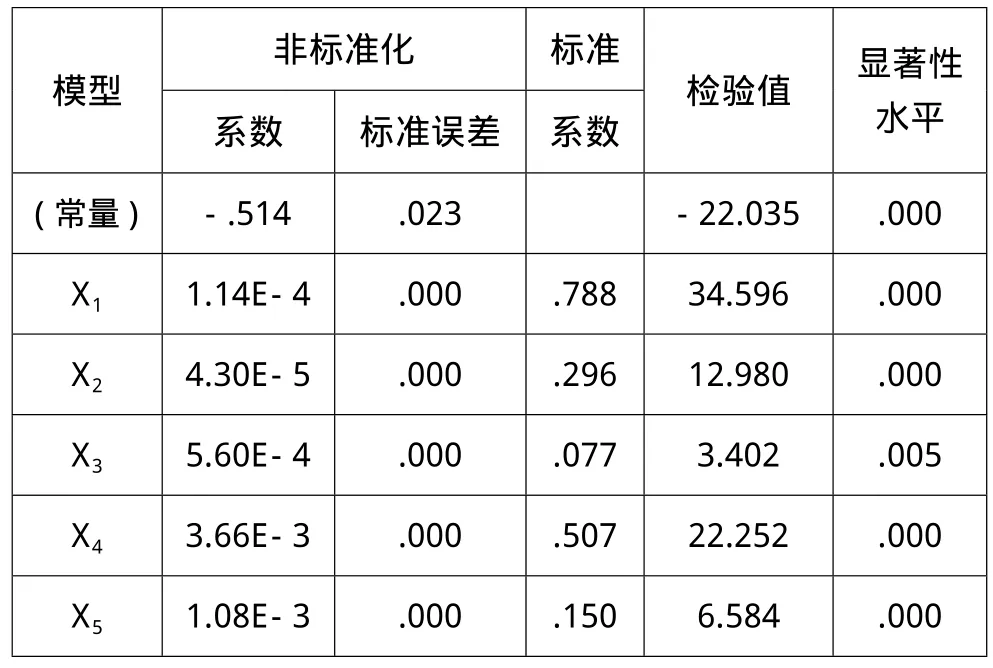
表5 回归系数表

表5为回归系数表，表中列出了变量X和常量的非标准化系数、标准化系数、检验值、显著性水平。由于所有变量的显著性水平均小于0.05，可认为所有变量对因变量f均显著，根据表中的非标准化系数，得到f与变量X的关系式为：

运用相同的方法可以得到其他因变量显著性回归方程式。

2.3 参数优化数学模型

选取设计变量、列出目标函数、给定约束条件后便可构造最优化设计的数学模型。任何一个最优化问题均可归结为：在满足给定的约束条件下，选取适当的设计变量X，使其目标函数f（X）达到最优值。目标函数的最优值一般可用最小值的形式来体现。因此，最优化设计的数学模型表达式为[9]：

在结构设计中常以减小质量为目标，最优化设计的目标函数为质量，则问题就成为求目标函数的最小值，根据前面的分析和构造的目标函数和约束函数，得出塔架轻量化设计的数学模型完整表达式为：

3 优化模型求解

经过理论分析与试验设计，建立塔架结构优化的数学模型。下一步的工作就是在此基础上选择合适的算法对模型进行优化求解。利用MATLAB软件的优化设计工具箱[10]的优化算法，可以求解该优化数学模型。

3.1 MATLAB软件优化算法

MATLAB软件是一种面向科学与工程的高级语言，运用它所提供的优化工具箱求解机械优化问题，与传统的求解机械优化问题的方法相比有很大优越性。

利用MATLAB软件的优化设计工具箱来求解优化问题，可以节省编制优化程序的时间。利用文件编辑器来编写目标函数及约束函数，然后调用相应的优化函数，系统即可自动运行求出最优解。

该软件还可以避免优化方法选择不当而造成无法得到最优解。在这个工具箱中，对每一种函数每一步的求解都是通过选择一种最佳方法来进行的。针对本文线性约束优化问题，选择的方法是线性规划法。

3.2 MATLAB优化函数

在MATLAB软件的优化设计工具箱中，用于求解线性约束优化的数学模型形式如下[11]：

函数是linprog，其主要格式为：

[x，fval]=linprog（f，A，b，Aeq，beq，LB，UB，x0，options）

其中x、b、beq、LB、UB是向量，A、Aeq为矩阵。

x：输出的最优解

fval：当最优解为x时的最优值

x0：初始值

3.3 优化结果分析

将塔架数学模型输入MATLAB软件,经过若干次迭代后，得到如下优化结果：

为验证优化结果的有效性，将该优化后的参数组合再进行有限元分析，得出分析后的塔架极限最大应力、疲劳损伤值、模态一阶频率和屈曲安全系数。如表6所示。

由表6可知，优化后塔架极限最大应力增加了9.53%，优化值为220.12MPa，小于材料许用应力304.5MPa，满足极限强度要求。疲劳损伤值增加了19.12%，优化值为0.947，小于1，塔架在设计寿命内不发生疲劳破坏。模态一阶频率减少了6.67%，优化值为0.364Hz，小于风电机组切入转速时频率0.417Hz，故塔架与机组不发生共振。屈曲安全系数发生了大幅减少，优化值为1.5416，大于1，塔架不发生屈曲破坏。

经验证，优化参数结果满足塔架结构极限应力、疲劳、屈曲和模态要求，由此得到塔架质量的优化后结果，如表7所示。塔架质量降低，取得了良好的优化效果，该结果具有重要的现实意义和参考价值。

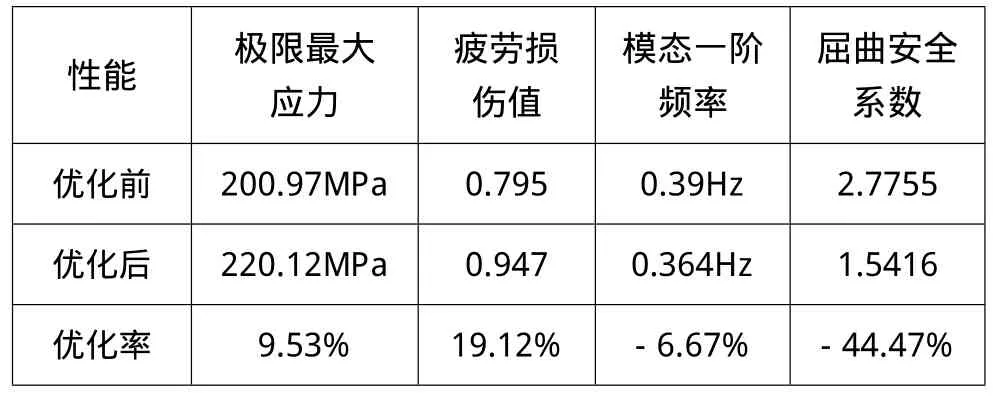
表6 塔架性能优化结果

表7 塔架质量优化结果（单位：t）

通过应用正交试验设计方法和优化设计算法来对塔架结构进行优化设计，大大减少优化过程中的复杂计算过程，极大压缩了计算工作量，且取得了满足实际需要的结果。

4 结论

本文运用正交试验设计，建立试验模型，根据正交试验的结果，运用数据统计分析软件SPSS18.0进行多元线性回归分析，建立了优化模型的目标函数、设计变量和约束条件，结合工程实际确定了设计变量的取值范围，最终建立塔架结构优化的数学模型。在此基础上，应用MATLAB优化工具箱对模型进行求解，得到了优化结果。在满足塔架结构极限应力、疲劳、屈曲和模态要求的前提下，减轻了8.93%的塔架质量。

[1] 陆萍,秦惠芳等.基于有限元法的风力机塔架结构动态分析[J].机械工程学报,2002,38(9 ):127～130.

[2] 兰勇,郭彦林.梭形钢管格构柱弹性屈曲性能[J].建筑结构学报,2002,23(5):18～24.

[3] 董小瑞,苏铁熊.不同结构曲轴的疲劳强度分析[J].车用发动机,2002,3:29～31.

[4] 王新敏.ANSYS 工程结构数值分析[M].北京: 人民交通出版社, 2007.

[5] 朱燕堂, 赵选民, 徐伟.应用概率统计分析.西安: 西北工业大学出版社,2004.

[6] 赵选民.试验设计方法[M].北京: 科学出版社,2009.

[7] 孙靖民, 朱成秋.机械结构优化设计[M].哈尔滨: 哈尔滨工业大学出版社,1985.

[8] 吴培乐译.经济管理数据分析实验教程spss18.0操作与应用[M].北京:科学出版社,2012.

[9] 刘惟信.机械最优化设计[M].北京: 清华大学出版社,1994.

[10]施阳,李俊.MATLAB语言工具箱[M].西安: 西安工业大学出版社,1997.

[11]周开利,邓春晖.MATLAB基础及其应用教程[M].北京: 北京大学出版社,2007.