一种实用的超短期光伏发电预测方法
2013-04-26汤义勤马红伟毛建容
孙 锐 汤义勤 马红伟 毛建容
(1.许继集团有限公司,北京 100085;2.台州电业局,浙江 临海 317000)
光伏发电作为清洁能源,既能满足经济社会发展带来的对能源的需求,又能减少化石燃料的污染,因此得到日益广泛的应用。但是光伏发电受外部天气等因素影响较大,发电功率存在很大的不确定性,波动性较大[1-2]。对光伏发电系统发电量进行预测,有助于含光伏发电的电力系统的安全、经济运行,并且光伏出力的预测结果可辅助电网的各种运行控制决策,提高含光伏发电电网的稳定性[3-5]。
光伏发电功率与很多因素有关,包括光伏电池的型号、阵列的面积、表面污染程度、季节变化、气象因素、太阳辐射等,这些因素与发电功率之间为复杂的非线形关系,且相互之前存在多种耦合,确定模型非常困难[6-7]。目前对于光伏发电超短期预测的研究很多,主要集中在非线性算法方面,包括神经网络法[8]、最小二乘相量机法[9]和智能法等。考虑到在线计算的速度、效率,以及光伏电站建成后,其内部特性基本稳定,发电功率只与太阳辐射强度、温度等气象因素有关[10],因此本文提出一种通过气象因素找到历史相似日,然后根据相似日的历史数据取得光伏发电功率的典型变化趋势,从而求取预测功率的方法。
1 超短期功率预测算法
在当前时刻功率值已知的情况下,求预测时刻功率的变化,就得到预测结果。
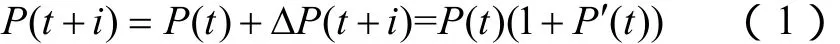
式中,P(t+i)为ti+时刻的发电功率预测值;P(t+i)为t时刻的实际发电功率值;ΔP(t+i)为t+i+时刻相对t时刻的预测功率变化值;P′(t+i)为t时刻到t+i+时刻的变化率
由于P(t+i)已知,预测关键是获得P′(t+i)。由相似日的样本数据,得到相似日P′typ(t+i),从而求得预测功率。因此求取相似日,并由相似日得到典型变化趋势P′typ(t+i)是关键。
2 相似日模型
得到典型变化趋势首先要选定相似日。相似日采用相关度的大小进行选取[11]。由气象部门或者专业的机构获取数值天气预报,提供的天气预测信息,基本包括天气类型、辐射强度、温度、湿度等。因此可先根据天气类型筛选出一部分历史日,结合就地气象系统的采集数据,可以获得历史日准确的天气信息样本。天气类型分为晴天、雨天、阴天[12]。先选取出与预测日相同天气类型的历史日,然后通过计算相关度来确定相似日。
用x0(1)、x0(2)两个向量分别表示待预测日的辐射强度和温度。历史数据中某一天的两个影响因素构成的向量为xj=[xj(1),xj(2)]。则x0与xj的温度因素关联系数为
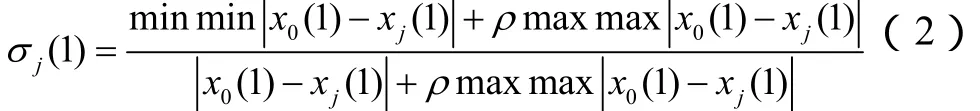
式中,ρ是分辨系数,一般取值 0.5。定义x0与xj的相似度为

从临近的历史日开始,逐一计算与待预测日的相似度,并比较,相似度jδ最大的历史日作为待预测日的相似日。根据区域间光伏发电特性不同,权重系数的设置不同,算法中的权重系数需要大量的实测数据,通过误差分析反复调整得到相对稳定的值。
选择相关度最大的前k个数据记录作为相似日来计算典型的曲线变化趋势,即
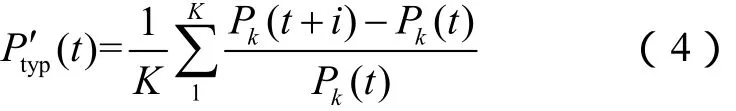
3 数据预处理
历史样本数据的预处理包括两个部分,一部分是坏数据的处理,包括奇异数据、毛刺等,这些坏数据如果参加计算必然会影响预测结果的准确性;另一部分是因为系统的计划、临时的策略引起的数据“不一致性”,比如光伏电站的临时限电措施、定时的检修计划等。辨识和修正这些数据才能确保预测的准确性。
3.1 历史坏数据的判别及处理
对样本数据进行处理,去除奇异的数据。
对于每个相似日的发电功率,根据预测间隔设置I个采样点,设第n个相似日样本第i点数据P(i,n),其中,i=1,2,…,I;n=1,2,…,M。
首先用中位数法获得M个样本典型发电功率数据Ptyp(i),i=1,2,…,I。即将P(i,n)对每点M个相似日样本排序得到Psort(i,M),则
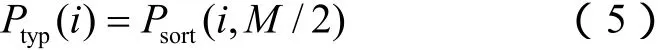
样本坏数据计算方法有:
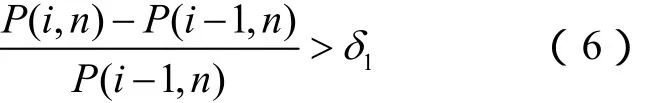
即功率变化过大则判定为奇异数据,其中δ为功率变化的上限。
针对判定出来的坏数据,进行数据恢复:
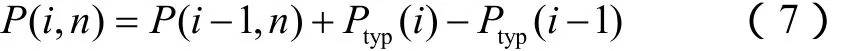
3.2 限电及检修计划
选取历史日的样本数据时,首先要读取限电及检修计划,判断历史日是否参与了限电或者检修计划。如果某历史日采取了限电措施,则该日不能作为相似日的历史样本。如果某历史日电站的部分阵列进行检修,应当将历史数据按照检修容量比例扩大,计算出额定容量下的发电功率,公式为

式中,Pfac为样本的实际发电功率,Ctotal为系统的额定容量,Cfact为历史日实际投入的发电容量,考虑到样本当日实际的光伏发电投入容量,得到单位容量的发电功率。通过计算得到额定容量下的发电功率。
4 案例分析
将本文算法选用河南省某微电网示范工程的光伏系统中进行验证。该案例为380kW光伏系统,在实际应用中以 15min作为超短期预测计算的步长,预测2011年8月9日的光伏发电超短时出力。
如图1所示,超短时发电预测流程主体包括三大部分:相似日选取、发电功率预测、误差分析。启动后,首先判断是否满足相似日计算的条件,将预测日前的15天作为样本选择的范围,在此范围内选择与预测日相同天气模型的历史日作为相似日样本,进行加权距离的计算。将计算结果进行排序,选择加权距离最小的 3个历史日作为超短时相似日样本,获取样本的发电功率数据,先进行数据预处理,然后根据算法得到典型变化趋势P′typ(t+i)。
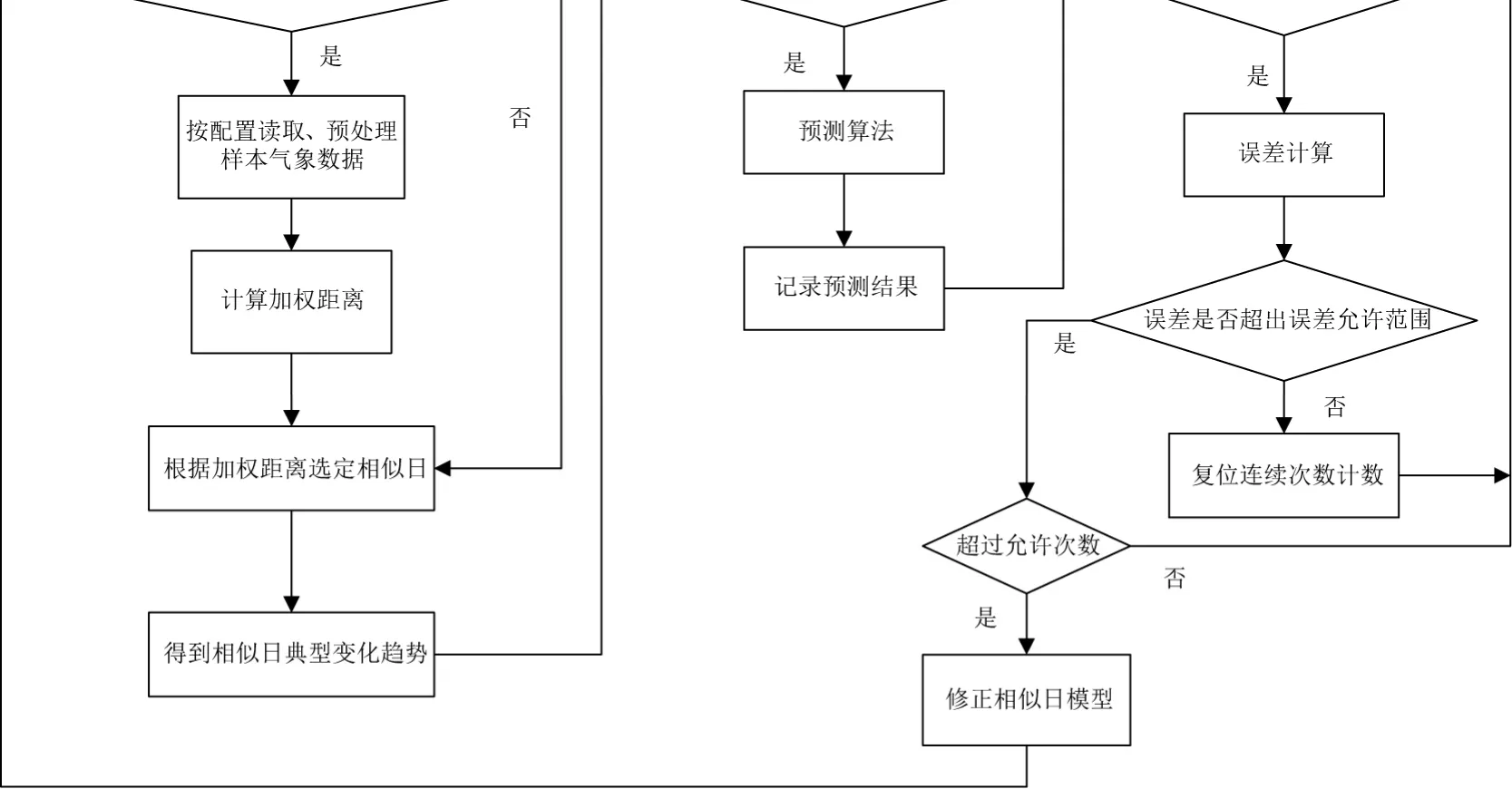
图1 超短期预测流程图
以15min为间隔进行发电功率预测,由当前时刻的发电功率,以及典型变化趋势P′typ(t+i),按照超短时算法,得到预测功率P。
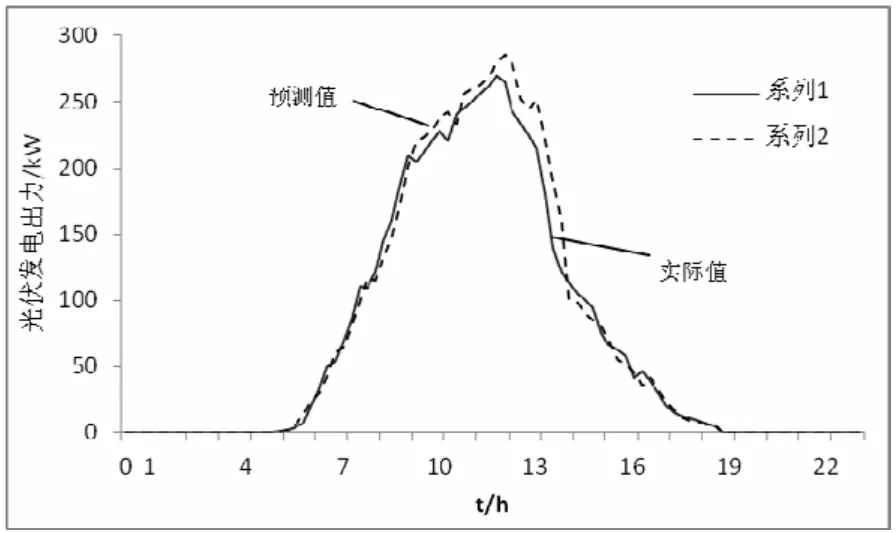
图2 预测结果及实际值
对于预测的结果进行误差分析,判断误差是否在允许的范围内,如果误差超出允许范围的连续次数超过配置要求,则重新选择天气模型进行相似日计算。因为天气模型是由该日从气象中心获得的预报天气确定,可能不准确,或者天气发生剧烈变化。因此当预测误差偏大时,则调整天气模型,选择与预报天气最相近的天气模型进行预测,调整天气模型的顺序:晴、多云、阴、雨。另外当天气发生突然变化时,进行天气模型的转换也能够提高预测的准确度。
本文采用绝对百分比误差(APE)和平均绝对百分比误差(MAPE)对预测值进行比较分析,则
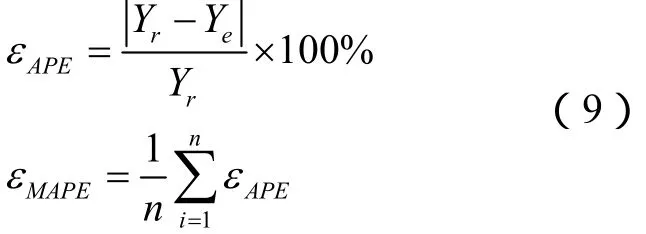
由图2可看出光伏有效出力的时间段为06:00-18:00,其余时间出力均为 0。因此仅针对该时间段内的数据进行误差分析。
表1是每15min的预测结果。其中,预测值平均绝对误差为11%。
图2与图3给出了实际值与算法预测值,及误差分析。分析以上结果可知:
1)从平均绝对误差值看,具有较高的预测精度;
2)08:00-14:00的预测精度较高,但06:00-07:00和15:00-16:00两个时间段的预测误差比较大。从实际结果分析可以推断出,由于云量等偶然因素造成的短暂的天气波动,使当前发电功率与典型变化趋势不一致时,使预测功率“随波逐流”,上下波动,误差偏大的情况。但平均绝对误差在20%以下,还是具有一定的推广和应用价值。
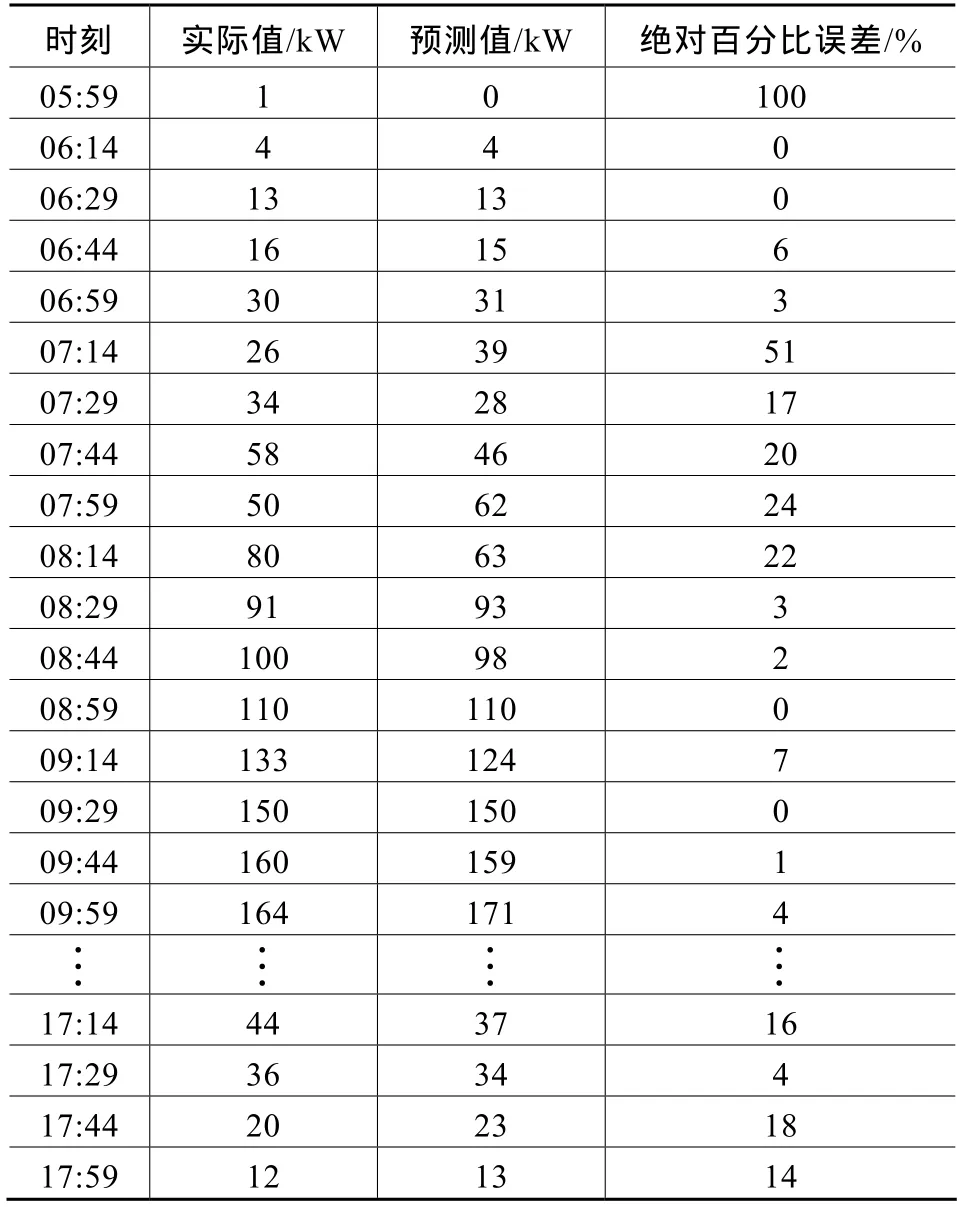
表1 预测结果
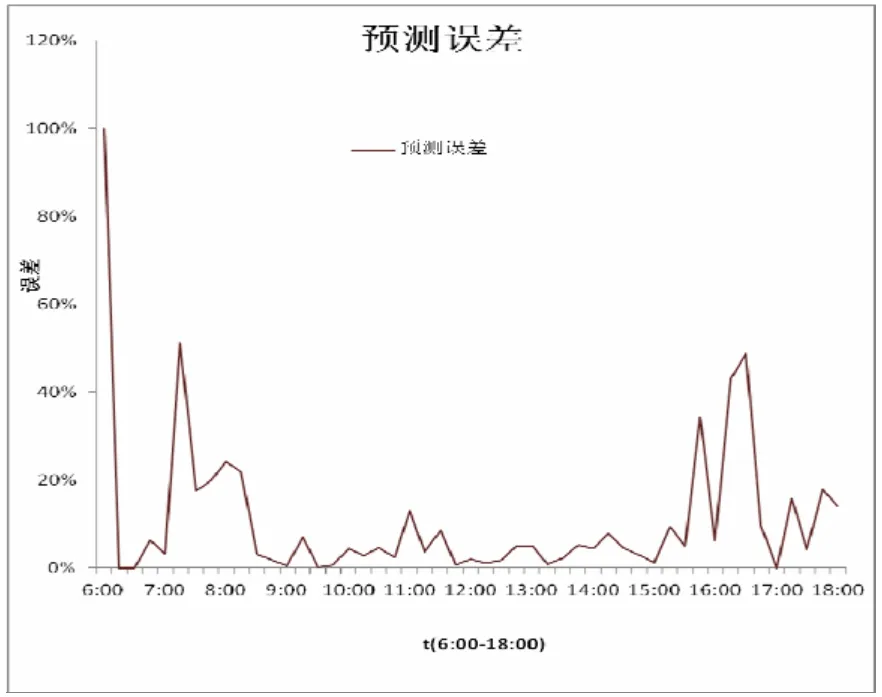
图3 误差曲线
5 结论
本文提出了一种实用的基于相似日典型趋势方法进行超短期光伏发电预测,通过对实际发电数据进行预测表明,该算法简单、可靠、实用,运算速度快,精度高。但是对于数值天气预测的精度要求较高。在天气剧烈变化期间,天气预测精度会有所下降,相应的功率预测的精度也随之降低。但是随着数值气象预报系统的发展,光伏电站就地气象系统能够采集到云层的厚度,并且通过对采集的数据进行分析,能够就地对天气变化进行预测,必然能够大大提高在天气剧烈变化期间算法的精确程度。
[1] 金焕,于化丛,葛亮.太阳能光伏发电应用技术[M].北京电子工业出版社,2009:13-14.
[2] KIM I S,KIM M B,YOUN M J.New maximum power point tracker using sliding mode observer for estimation of solar array current in the grid-connected photovoltaic system[J].IEEE Transaction Industrial Electronics,2006,53(4) : 1027-1035.
[3] 李冬辉,王鹤雄,朱晓丹,等.光伏并网发电系统几个关键问题的研究[J].电力系统保护与控制,2010,38(21):208-214.
[4] 周念成,闫立伟,王强钢.光伏发电在微电网中接入及动态特性研究[J].电力系统保护与控制,2010,38(14):120-127..
[5] TSIKALAKIS A G,HATZIARGYRIOU N D.Centralized control for optimizing microgrids operation[J].IEEE Transactions on Energy Conversion,2008,23(1):241-248.
[6] 徐维.并网光伏发电系统数学模型研究与分析[J].电力系统保护与控制,2010,38(10):17-21.
[7] 李光明,廖华,李景天,等.并网光伏发电系统发电量预测方法的探讨[J].云南师范大学学报,2011,31(2):33-38.
[8] 陈昌松,段善旭,殷进军.基于神经网络的光伏阵列发电预测模型的设计[J].电工技术学报,2009,24(9):153-158.
[9] 朱永强,田军.最小二乘支持向量机在光伏功率预测中的应用[J].电网技术,2011,35(7):54-59.
[10] 杨杨超,榑沼弘贵.光伏发电系统发电量的预测方法[J].智能建筑电气技术,2011,5(2):30-34.
[11] 黎灿兵,李晓辉,赵瑞,等.电力短期负荷预测相似日选取算法[J].电力系统自动化,2008,32(9):69-71.
[12] 李军,许继生,王生渊,等.一种并网型光伏电站光功率及发电量预测的方法[J].青海电力,2010,29(2).
