欠驱动航天器滑模速率阻尼控制*

欠驱动航天器是指执行机构产生独立控制力矩的维数小于运动自由度维数的航天器，对欠驱动航天器姿态控制方法的研究具有重要的意义.一方面可以提高航天器控制系统的可靠性，保证航天器在故障情况下仍能正常执行任务，另一方面可以减轻控制系统重量、减小体积、降低成本.

对欠驱动航天器最早的研究可以追溯到1984年，Crouch[1]在基于微分几何理论对刚体航天器的可控性进行了深入研究，后来在其基础上，Krishnan[2]和Wang[3]分别给出了推力器控制输入为二维和一维时航天器姿态可控的条件.目前已有很多文献针对推力器执行机构的欠驱动航天器，设计了角速度稳定控制器和三轴姿态稳定控制器.Victoria在文献[4]中对动力学模型展开研究，设计了滑模变结构控制器实现角速度稳定.张兵等[5]以非完整配置的单向推力器系统为执行机构，设计了姿态去翻滚滑动控制器.文献[6]只对动力学进行分析，基于Lyapunov直接法设计了“fail-safe”角速度稳定控制律.另外文献[7-8]分别用不同的方法设计了全姿态稳定控制律.但上述这些文献对工程实际应用因素考虑较少，并且大部分只针对对角惯量阵进行研究.

本文针对仅具有两维推力器控制输入且欠驱动轴不是对称轴的欠驱动航天器，设计了滑模变结构速率阻尼控制器，实现了欠驱动航天器的角速度阻尼.与文献[6，9]提出的控制律相比，本文基于滑动模的镇定策略有非常强的鲁棒性，有更高的应用价值.本文的控制方法是在文献[4]滑模控制方法基础上提出的，借鉴了其滑动模选取方法.与已有的滑模控制相比，本文研究了控制器参数与控制效果之间的内在关系，给出了参数选取原则，得到了更合理的参数和更好的仿真结果.并且文中对滑模控制器的稳定性和抗干扰性能进行了分析，证明了该控制律对非对角质量特性航天器控制的可行性.最后，在考虑了执行机构开关特性、角速度测量幅值受限和外界干扰的情况下，基于Matlab工具进行了控制仿真，证实了算法的有效性和工程实用性.

1 数学模型

1.1 姿态运动模型

考虑一个刚体航天器，只有推力器执行机构.若有一轴推力器失效，不失一般性假设第3轴推力器失效τ3=0，则在航天器本体坐标系下动力学方程可写为：

(1)

其中，J=diag{I1,I2,I3}为航天器对角惯量阵；ω=[ω1,ω2,ω3]T为航天器角速度矢量在本体系的表示；τ=[τ1,τ2,0]T为推力器控制力矩在本体系的表示；τdis=[τdis1,τdis2,τdis3]T为干扰力矩在本体系的表示.

若忽略干扰力矩τdis，并设

(2)

则式(2)可简化为

(3)

式中α为航天器的不对称系数，表示欠驱动航天器的非轴对称性，其绝对值的大小代表了对欠驱动轴的控制难度，α的绝对值越小控制难度越大，α为零时欠驱动轴将完全无法控制.

1.2 推力器模型

考虑喷气执行机构实际工作时的开关特性，要通过脉宽调制(PWM)将连续的控制力矩转换为实际需要的脉宽信号.PWM调制器如图1所示，A代表输入到PWM调制器的控制力矩，Amin代表最小输入力矩，Amax代表最大输入力矩，T代表控制周期，τ代表推力器最小工作脉宽.在每个控制系统的采样周期内，PWM调制器根据输入的大小确定控制姿控推力器的脉宽长度，而脉宽的符号确定姿控推力器产生控制力矩的方向.

2 滑模控制律设计

以简化模型(3)为对象，设计滑模控制律.取滑动模函数为

(4)

可见，一旦到达滑模面(s=0)，z轴(欠驱动轴)角速度将按指数规律收敛.

下面就是要设计控制输入u1和u2，驱动系统到达滑模面s=0，并保持在滑模面上.取李雅普诺夫函数为V(s)=s2/2，显然当s≠0时V(s)>0.

=s(αω2u1+αω1u2+k1αω1ω2)

(5)

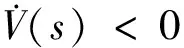
(6)

此时，

(7)

所以到达滑模面后三轴角速度将按以下指数规律运动：

(8)

显然为了保证系统收敛，参数必须满足k1>k2>0.

综上可知，在选取控制参数满足条件

k1>k2>0，k3>0,k4>0

(9)

时，系统是渐近稳定的.

滑模控制器有一个突出问题就是抖振问题[10]，这里通过将符号函数替换为饱和函数来克服抖振，此时控制律变为

(10)

其中饱和函数定义为如下形式：

(11)

ε越大克服抖振能力越强，但是会降低控制精度，所以对参数ε的选取要权衡这两方面因素.

3 滑模控制律分析

3.1 滑模控制参数选取指导原则

观察模型(3)和控制律(6)可知，系统在到达滑模面之前驱动轴角速度按如下规律运动：

(12)

显然ω1和ω2可能会出现一个恒值段

(13)

由式(13)得到，两轴出现恒值段的角速度为

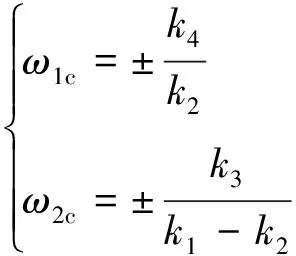
(14)

在这一段时间内，

(15)

可以看出|ω1c|和|ω2c|的大小直接影响了s的收敛特性，也直接影响了欠驱动轴的收敛快慢.一般|ω1c|和|ω2c|选的越大，欠驱动轴的角速度收敛越快，但是由于实际中控制力矩受限和角速度测量幅值受限的限制，选择过大会导致系统振荡甚至发散不稳定，而且一般|ω1c|和|ω2c|选择越大消耗燃料越多，会缩短航天器的在轨寿命.所以要综合权衡以上因素，参照式(14)适当选择控制器参数，将|ω1c|和|ω2c|配置到恰当位置，以产生较好的控制效果.

3.2 抗干扰性分析

首先做如下假定：三轴干扰都是有界的，设udisi(i=1,2,3)为三轴的外界干扰，|udisi|max(i=1,2,3)分别为三轴干扰的绝对值上界，则有下式成立：

|udisi|≤|udisi|max，(i=1,2,3)

(16)

考虑带外界干扰的简化模型如下：

(17)

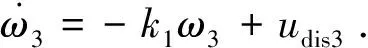
=-k3(sαω1)sgn(sαω1)-

k4(sαω2)sgn(sαω2)+

sαω1udis2+sαω2udis1+sk1udis3

=-k3|sαω1|-k4|sαω2|+sαω1udis2+

sαω2udis1+sk1udis3

≤-(k3-|udis2|max)|sαω1|-

(k4-|udis1|max)|sαω2|+sk1udis3

(18)

另外，随着ω1,ω2趋于零，系统对ω3的鲁棒性逐渐消失.但是，总是调整参数使欠驱动轴角速度ω3早于ω1，ω2收敛到零.当ω1,ω2趋于零后，说明已完成对ω3的阻尼控制，之后不能保证对ω3的鲁棒性，要及时切换到其他姿态控制方式.

3.3 非对角惯量阵问题分析

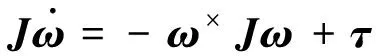
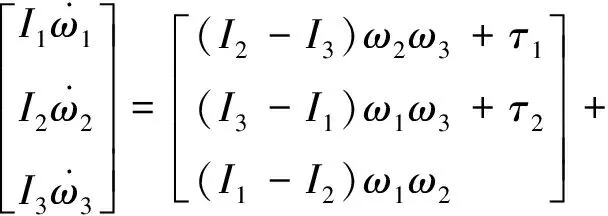
(19)

4 仿真结果与分析

本节基于MATLAB仿真工具进行数值仿真，对上述控制算法的有效性和可行性进行验证.

4.1 质量特性取对角阵的情况

控制律是根据对角阵的情况推导，首先以质量特性为对角阵的航天器作为被控对象验证控制律的有效性.航天器的质量特性选为J=diag{1100,2800，2900}kg·m2.外干扰力矩τdis取均值为0，标准差为0.025的正态分布的随机干扰如图2所示.

为了验证算法的工程实用性，执行机构采用喷气PWM控制仿真，选取控制周期0.5s，最小喷气脉宽0.025s，喷气力矩2N·m.考虑工程中角速度测量幅值受限，取受限幅值为0.035rad/s.初始角速度选为：[ω1(0)ω2(0)ω3(0)]T=[0.06 -0.06 0.06]Trad/s，控制器参数选为：k1=0.5,k2=0.1,k3=0.013,k4=0.0027,ε=0.00005.相应的仿真曲线如图2～6所示，从图3可以看出，在偏航轴的推力器失效情况下，仅通过另两轴的喷气控制力矩实现了三轴角速度阻尼.因为对欠驱动轴的控制是通过它与另两轴的耦合关系来实现的，所以欠驱动轴的角速度必须比另两轴提前收敛到零.观察x轴和y轴角速度曲线，容易发现二者都有一个恒值段，这个恒值的大小是由4个控制参数决定的，具体关系见3.1节的介绍.结合图4看出，在150s附近基本到达滑模面，之后x轴和y轴角速度近似按式(8)描述的指数规律收敛.图4为滑动模s的变化曲线，由于推力器的输出力矩受限，所以在开始段滑动模s没有按照预期趋势收敛，随着期望控制力矩与实际喷气力矩的接近，在100s后s近似按抛物线规律迅速收敛到零.

图5和图6显示了x轴和y轴的喷气控制力矩情况，以图5为例简要说明.在0～25s时间内x轴推力器持续反向喷气，一直输出-2N·m的控制力矩.在25～140s时间内曲线很密，反映了推力器频繁开关，输出小于2N·m的等效力矩.由于推力器具有开关工作特性，可以实现输出力矩的突变，所以该系统很适合采用滑模变结构控制.

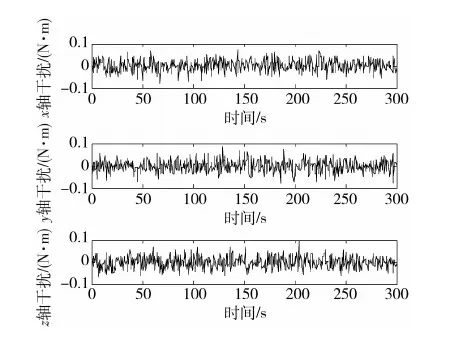
图2 三轴干扰力矩

图3 三轴角速度响应曲线

仿真结果显示，加入随机干扰没有改变控制系统的稳定性，只是对控制精度有一定影响.仿真中还增加了角速度测量幅值受限，这也并没有改变控制器的控制效果.这些都体现了滑模控制器有很强的鲁棒性，适用于工程应用.

4.2 质量特性取非对角阵的情况

为验证该控制律对于非对角被控对象的控制效果，选取航天器的质量特性使惯量积占惯量的20%左右

相应的仿真曲线如图7～11所示.

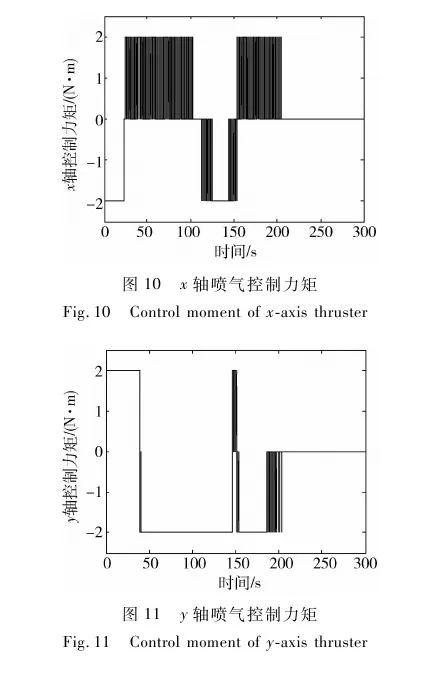
图7显示了惯量积等效干扰力矩的大小变化，易看出三轴等效干扰幅值在0.6N·m以内，并且随着三轴角速度的收敛等效干扰力矩也逐渐减小到零.

由图8～11的仿真结果可看出，虽然控制律按对角阵设计，但应用于非对角惯量阵航天器仿真仍然有效.正如3.3节分析的那样，将惯量积部分视为外界干扰处理，这样就转化为对角惯量阵航天器的控制律设计问题.由于滑模变结构控制器具有很强的鲁棒性，完全可以抵抗这一等效外界干扰，所以该控制律对于非对角惯量阵航天器的控制也同样有效.这为解决非对角质量特性航天器的欠驱动控制问题提供了一种解决思路.

5 结束语

一旦航天器因故障高速翻滚，必然要先阻尼角速度然后再调整姿态，所以对欠驱动航天器角速度阻尼的研究非常必要.本文针对有一轴推力器失效的欠驱动航天器，设计了滑模速率阻尼控制器.通过理论证明和仿真验证证实，在欠驱动航天器出现翻滚失控的情况下，该控制器可以实现对其角速度阻尼，最终将航天器三轴角速度稳定在零附近.并且该控制器可以实现对非对角阵航天器的速率阻尼控制.本文中的控制器参数是在反复试验的情况下得到的一组较理想的参数，但是在同时考虑燃料消耗和控制效果两种因素时，是否能找到一组最优的控制器参数是有待解决的问题.

参 考 文 献

[1]Crouch P E. Spacecraft attitude control and stabilization：applications of geometric control theory to rigid body models[J]. IEEE Transactions on Automatic Control, 1984, 29(4): 321-331

[2]Krishnan H, McClamroch H, Reyhanoglu M. On the attitude stabilization of a rigid spacecraft using two control torques[C]. American Control Conference, Chicago, USA, 1992

[3]Wang D X, Jia Y H, Jin L. Controllability of an underactuated spacecraft with one thruster under disturbance[J]. Acta Mechanica Sinica, 2012, 28(3): 838-847

[4]Victoria C C. Detumbling and reorienting underactuated rigid spacecraft[J]. Journal of Guidance Control and Dynamics, 1996, 19(3):708-710

[5]张兵，吴宏鑫. 非完整配置下姿态翻滚抑制的滑动控制[J]. 宇航学报, 2000, 21(2):35-42

Zhang B, Wu H X. Sliding mode control for attitude detumbling under incomplete configuration[J]. Journal of Astronautics, 2000,21(2):35-42

[6]Eshaghi R, Paul K C W , Fred Y H. A Lyapunov-based fail-safe controller for an underactuated rigid-body spacecraft[C]. AIAA Guidance, Navigation and Control Conference, Montreal, Canada, 2001

[7]Behal A, Dawson D, Zergeroglu E, et al. Nonlinear tracking control of an underactuated spacecraft[J]. Journal of Guidance Control and Dynamics, 2002, 25(5): 979-985

[8]林壮,段广仁. 欠驱动刚体航天器姿态机动滑模控制研究[J]. 控制与决策, 2010, 25(3): 389-393

Lin Z , Duan G R. Research on sliding mode control for underactuated rigid spacecraft attitude maneuver[J]. Control and Decision, 2010, 25(3): 389-393

[9]Aeyeles D .Stabilization of a class of nonlinear systems by a smooth feedback control[J]. Systems and Control Letters, 1985, 6(1): 289-294

[10]高为炳. 变结构控制的理论及设计方法[M]. 北京：科学出版社, 1996