基于分段瞄准点预报显式制导的月地返回轨道中途修正研究*
2013-04-26周亮,胡军
在月地返回过程中,探测器受入轨置入误差、导航误差、执行误差以及模型误差等多种误差源的影响,飞行的实际轨道不可避免地偏离精确设计中得到的标称轨道,因此需要对其进行中途修正.在地月转移轨道的中途修正方法[1-2]和实践[3-5]已经积累的比较成熟的前提下,考虑更复杂的约束条件及更大的误差偏差情况,进行月地返回轨道中途修正的研究,可为中国深空探测的发展奠定基础.
现有中途修正方法[6-9]大都采用基于小偏差的摄动制导法,通过计算误差传递函数的雅克比矩阵得到所需速度偏差与目标值偏差的定量关系,从而得到所需的修正速度.其中,文献[6]基于此方法,完成了月地返回轨道的中途修正的研究,其结果能够满足月球采样返回任务对大气再入参数及落点位置的要求.相比摄动制导法,显式制导法算法简单,使用灵活,文献[10-11]利用显式制导法,分别解决了传统地月转移轨道中途修正和基于平动点的低耗能地月转移轨道中途修正问题.然而对于月地返回轨道,由于其终值条件需要满足地球大气层再入的初值要求,约束条件复杂;且受月球驻留轨道交会对接及深空测控影响,其初始置入误差、导航误差更大,并未有文献基于显式制导对月地返回轨道的中途修正问题进行研究.
本文考虑月地返回轨道的特殊性,采用月球段及地球段分段进行中途修正的策略,基于瞄准点预报的显式制导法,给出了基于分段瞄准点预报显式制导的月地返回轨道中途修正方案.该方案有效地解决了月地返回轨道的中途修正问题,与摄动制导法相比,其算法简单,能够显著减少计算时间.仿真结果验证了该方案的有效性和优越性.最后给出了本文的结论.
1 基于分段瞄准点预报显式制导的月地返回轨道中途修正
1.1 数学模型
考虑在月球段及地球段的二体轨道动力学方程如式(1)和式(2)所示,分别建立在其中心天体的赤道惯性坐标系中.
(1)
(2)
式中rmp为探测器相对月球的位置矢量,r为探测器相对地球的位置矢量,μm,μe分别为月球和地球的引力常数.
多体模型除要考虑月球、地球的中心引力外,还包括N体引力、地球非球形、月球非球形、太阳光压和大气阻力等摄动因素.在地心赤道惯性坐标系中,多体模型的轨道动力学方程如式(3)所示:
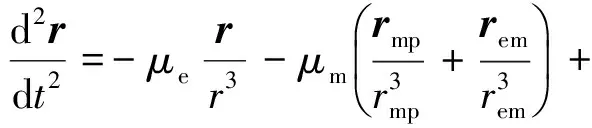
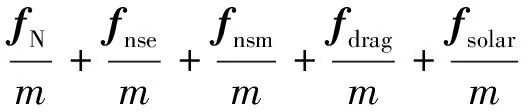
(3)
其中,rem为月球的位置矢量,右式中第一项、第二项分别为地球、月球中心引力加速度,m为探测器质量,fN是N体引力摄动力,fnse是地球非球形摄动力,fnsm是月球非球形摄动力,fsolar是太阳光压摄动力,fdrag是大气阻力摄动力.月地返回轨道的边值约束条件较地月转移轨道复杂,如表1所示[12].其中,hL,iL为驻月轨道高度和倾角;rZE为再入点地心距,λE,φE为再入点经度和纬度,θ为再入角,iE为轨道倾角.

表1 月地返回轨道的约束条件
1.2 基于瞄准点预报的显式制导法
基于瞄准点预报的显式制导法首先需要预报瞄准点,而后利用二体模型,计算修正点到瞄准点在给定转移时间的速度作为从修正点到标称轨道落点的实际需要速度.其示意图如1所示,计算流程图如图2所示,计算过程如下:
1)以修正点位置rC和速度vC为初始值,根据多体模型,按照给定的积分时间T,计算出多体模型偏差轨道落点位置rL1和速度vL1;
2)以修正点位置rC和速度vC为初始值,根据二体模型,按照给定的积分时间T,计算出二体模型偏差轨道落点位置rL2和速度vL2,则多体模型相对二体模型的影响为
ΔrL=rL1-rL2;
则得到预报瞄准点位置rM=rB-ΔrL,其中rB为标称轨道落点;
3)以修正点位置rC和预报瞄准点位置rM,根据二体模型,按照给定的转移时间T,依据求解Lambert问题的普适变量法,计算出所需的速度vCM,即为修正点到标称轨道落点的转移速度vCnew,所需速度增量为
ΔvC=vCnew-vC;
4)以修正点位置rC和速度vCnew为初始值,根据多体模型,按照给定的积分时间T,计算出偏差轨道落点位置rL1new和速度vL1new,当偏差轨道落点和标称轨道落点位置匹配时即rB=rL1new,则过程结束,否则取vC=vCnew,rL1=rL1new,返回步骤2,重新迭代计算,直至符合要求;
5)此时满足落点位置匹配,根据任务需要判断是否需要落点速度匹配,如需要则所需的速度增量为
ΔvL=vB-vL1new.

图2 基于瞄准点预报的显式制导法计算流程图
1.3 基于分段瞄准点预报显式制导的月地返回轨道中途修正方案
在基于瞄准点的显式制导法的计算流程中包含基于二体理论的速度求解,所以选择在月球段和地球段分别运用基于瞄准点预报的显式制导法.选择进行三次中途修正,之间的间隔为24h,第一次修正在入轨后12h,第二次修正在入轨后36h,第三次修正在入轨后60h.选择第一次修正的目标点为进行第二次修正时刻对应的标称轨道落点,第二次修正的目标点为进行第三次修正时刻对应的标称轨道落点,优势在于避免进行速度匹配.在中途修正策略确定后,即可以确定中途修正计算过程中的各个步骤的积分时间.
综上所述,基于分段瞄准点预报显式制导的月地返回轨道中途修正方案如下:
1)月心段轨道修正:月心段轨道包括一次轨道修正,以标称轨道入轨后36h状态为标称轨道落点,以偏差轨道入轨后12h状态为修正点,根据图2的计算流程图得到预报瞄准点位置,从而计算修正点所需速度.
2)地心段轨道修正:地心段轨道包括两次轨道修正,分别为以标称轨道入轨后60h状态为标称轨道落点,以第一次修正后24h状态为修正点,和以标称轨道入轨后72h状态即标称再入点为标称轨道落点,以第二次修正后24h状态为修正点,根据图2的计算流程图得到预报瞄准点位置,从而计算修正点所需速度.第三次修正后,再入点地心距、再入点经纬度与标称值一致,如再入角及再入轨道倾角符合要求,则结束,如不满足可采用如下牛顿迭代法对第三次显式制导结果进行修正.
以修正点位置rC和速度vC为初始值,按照给定的积分时间T,计算再入点参数qf=[rfi],其中r为再入点地心距,f为再入角,i为轨道倾角,qf=f(rC,vC),而后可以利用式(4)计算再入点参数的偏差Δqf
Δqf=q(vC)-q*
(4)

利用基于瞄准点的显式制导法可以保证落点与再入点位置一致,如经速度匹配则和再入点状态一致,然而速度匹配所需速度增量很小,且再入点速度很大,即绝大部分都无需进行速度匹配及对显式制导结果进行修正.基于瞄准点预报的显式制导法是通过二体轨道与多体轨道位置的偏差来引入瞄准点,从而求解需要的速度,与摄动制导法相比,基于瞄准点的显式制导法的优势在于其算法简单,更无需计算误差传递函数的雅克比矩阵,轨道积分运算次数少,计算快速,可有效减小星载计算机负荷.
2 仿真分析
2.1 算例仿真
标称轨道选取文献[12]中的算例,考虑多体模型,得到标称月地返回轨道再入点参数如表2所示,其中TZ表示再入点时刻.
对误差源进行如下设置:初始入轨位置误差为5km,入轨速度误差为5m/s;月心段导航位置误差为20m,导航速度误差为0.1m/s,执行误差为0.1m/s;地心段导航位置误差为10m,导航速度误差为0.05m/s,执行误差为0.05m/s,其中本文所有误差均包含三轴误差.如不经中途修正,可知无法再入地球.依据基于分段瞄准点预测显式制导的月地返回轨道中途修正方案,可以得到修正结果如表3所示,最终再入点参数如表4所示.

表2 标称月地返回轨道再入点参数

表3 中途修正所需速度增量

表4 中途修正后再入点参数
由仿真算例结果看出:该方案所需的速度增量为|Δv|=19.58m/s,而在相同的条件下,采用摄动制导法所需速度增量为|Δv|=13.37m/s;前两次所需的速度增量较大,原因在于初始误差较大;方案过程无需进行速度匹配及对显式制导法进行修正;再入点参数满足再入点约束要求,但由于存在导航误差及执行误差,与标称值有所差别.
2.2 蒙特卡洛仿真
可采用蒙特卡洛仿真评估基于分段瞄准点预报显式制导的月地返回轨道中途修正方案的适用性.设定随机误差变量的统计特性如表5所示.
以2.1节的标称月地返回轨道,考虑表5所示的随机误差统计特性,利用基于分段瞄准点预测显式制导的月地返回轨道中途修正方案,分别生成1000个偏差转移轨道样本,其蒙特卡洛仿真结果如图3所示.
再入点参数的置信区间如表6所示,中途修正所需速度增量的置信区间及平均迭代次数如表7所示.
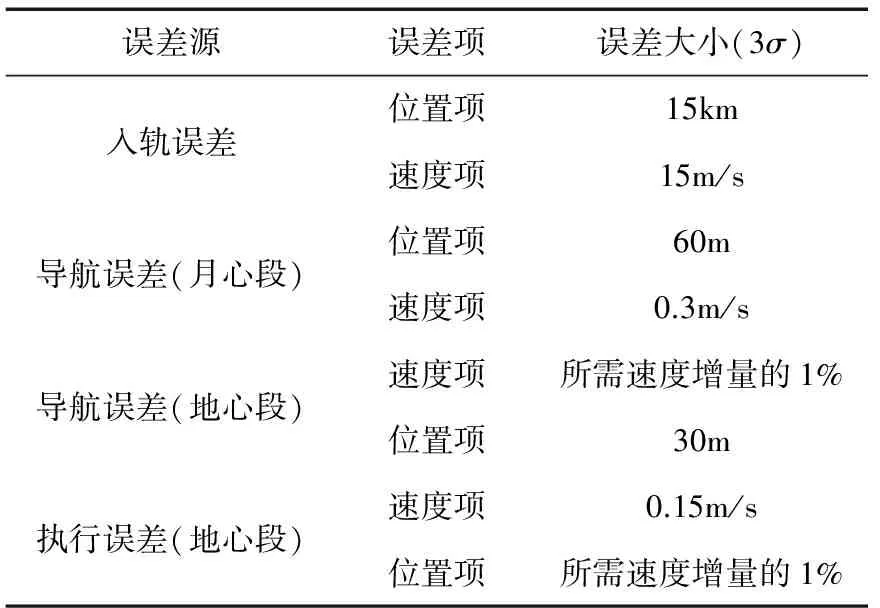
表5 月地返回轨道飞行中考虑的误差源特性
由蒙特卡洛仿真结果看出:该方案都能够满足再入点约束条件;在蒙特卡洛仿真过程中均无需进行速度匹配及对显式制导法进行修正,表明在一定误差允许范围内,方案具有很好的适用性;在相同的条件下,与摄动制导法得到的结果相比,所需速度增量有所增加,但迭代次数显著减少,可以有效减少计算时间,蒙特卡洛仿真表明计算时间比摄动制导法节省80%以上.

图3 基于分段瞄准点预报显式制导的月地返回轨道中途修正方案蒙特卡洛法仿真结果
表6中途修正后再入点参数置信区间
Tab.6 Confidence interval of reentry point parameters with midcourse correction

再入点参数rZE/kmθ/(°)λE/(°)φE/(°)iE/(°)1.3节方案置信区间(6499.096500.56)(-6.11-5.90)(42.1542.45)(4.755.03)(42.0842.12)

表7 中途修正所需速度增量置信区间及平均迭代次数
3 结 论
针对月地返回轨道的中途修正问题,本文给出基于分段瞄准点预报显式制导的月地返回轨道修正方案,通过理论说明,分析了该方案的优势,而后分别进行了算例仿真和蒙特卡洛仿真,得到了一些定量的结果.理论分析和仿真验证表明:
1)本文给出的基于分段瞄准点预测显式制导的月地返回轨道中途修正方案能满足再入点参数要求,其算法简单,计算快速;
2)与基于线性修正的摄动制导法相比,原理不同,所需速度增量略有增加,然而可以大大节省计算时间;
3)该方案能补偿导航误差及执行误差,在偏差不大的情况下,该方案都能保证落点位置匹配,速度基本匹配,无需进行落点速度匹配及对显式制导结果进行修正.
参 考 文 献
[1]周文艳, 杨维廉. 月球探测器转移轨道的中途修正[J]. 宇航学报, 2004, 25(1):89-92
Zhou W Y, Yang W L. Mid-correction of trans-lunar trajectory of lunar explorer[J]. Journal of Astronautics, 2004, 25(1):89-92
[2]谢剑锋. 地月转移轨道中途修正优化分析[C]. 全国第十二届空间及运动体控制技术学术年会, 桂林, 2006
[3]杨维廉, 周文艳. 嫦娥一号卫星地月转移轨道中途修正分析[J]. 空间控制技术与应用, 2008, 34(6):3-7
Yang W L, Zhou W Y. Analysis on midcourse correction of translunar trajectory for CE-1[J]. Aerospace Control and Application, 2008, 34(6):3-7
[4]杨维廉, 周文艳. 嫦娥一号月球探测卫星轨道设计[J]. 航天器工程, 2007, 16(6):16-24
Yang W L, Zhou W Y. Orbit design for lunar exploration satellite CE-1[J]. Spacecraft Engineering, 2007, 16(6):16-24
[5]周文艳, 杨维廉. 嫦娥二号卫星轨道设计[J]. 航天器工程, 2010, 19(5):24-28
Zhou W Y, Yang W L. Orbit design for chang’e-2 lunar orbiter[J]. Spacecraft Engineering, 2010, 19(5):24-28
[6]张磊, 于登云, 张熇. 月地转移轨道中途修正方法及策略[J]. 航天器工程, 2012, 21(3):18-22
Zhang L, Yu D Y, Zhang H. Method and strategy of the Moon-to-Earth trajectory midcourse correction[J]. Spacecraft Engineering, 2012, 21(3):18-22
[7]Hintz G R, Chadwick C. Design and analysis techniques for trajectory correction maneuvers [C]. AIAA/AAS Astrodynamics Conference, Seattle,Washington, August 20-22, 1984
[8]Cho D H, Chung Y S, Bang H C. Trajectory correction maneuver design using an improved B-plane targeting method[J]. Acta Astronautica, 2012, 72:47-61
[9]张晓文, 王大轶, 黄翔宇. 深空探测转移轨道自主中途修正方法研究[J]. 空间控制技术与应用, 2009, 35(4):27-33
Zhang X W, Wang D Y, Huang X Y. Study on the autonomous midcourse correction during cruise phase of interplanetary exploration[J]. Aerospace Control and Application, 2009, 35(4):27-33
[10]郗晓宁, 曾国强, 任萱, 等. 月球探测器轨道设计[M]. 北京: 国防工业出版社, 2001
[11]何巍, 徐世杰. 地月低能耗转移轨道中途修正问题研究[J]. 航天控制, 2007, 25(5):22-27
He W, Xu S J. Study on midcourse correction of low energy consumption Earth-Moon transfer orbit[J]. Aerospace Control, 2007, 25(5):22-27
[12]周亮, 胡军. 基于双曲线B平面参数的快速微分修正月地返回轨道精确设计[J]. 航天控制, 2012, 30(6):27-31
Zhou L, Hu J. Moon-earth return trajectory precise design of fast differential correction based on B-plane parameters of hyperbola[J]. Aerospace Control, 2012, 30(6):27-31
