空间飞行器大角度姿态机动优化控制*
2013-04-26马清亮,杨海燕,岳瑞华等
姿态机动对于空间飞行器完成精确定向、跟踪等期望的飞行任务至关重要[1].飞行器大角度姿态机动是一个具有强耦合性质的非线性控制问题.目前,应用于飞行器大角度姿态机动的非线性控制策略主要有变结构控制、动态逆控制、反演控制等[2-4].这些方法的理论基础主要是Lyapunov稳定性理论,其设计结果在很大程度上依赖于所构造的Lyapunov函数.为克服寻找Lyapunov函数的困难,文献[5]借助于平方和(SOS,sum of squares)优化技术,设计了用于飞行器大角度姿态机动的非线性镇定控制器.在考虑外部干扰的情况下,文献[6]进一步研究了飞行器大角度姿态机动的非线性H∞控制问题.但对于空间飞行器大角度姿态机动最优保性能控制问题,据作者所知,相关的研究成果尚未见报道.
本文在文献[5-6]的基础上,进一步研究飞行器大角度姿态机动的状态反馈最优保性能控制器问题.采用修正Rodrigues参数(MRP,modified Rodrigues parameters),以线性参数可变(LPV,linear parameter varying )系统的形式建立飞行器姿态运动模型;在分析系统性能指标的基础上,推导出状态反馈控制器存在的充分条件,并将控制器优化设计问题转化为一个具有平方和约束的参数优化问题.
1 问题描述
采用修正Rodrigues参数方法描述飞行器的姿态运动,具有结构简单、计算量小的优点.修正的Rodrigues参数可由四元数得到.设qi(i=1,…,4)为四元数参数,σi(i=1,2,3)表示修正的Rodrigues参数,e为刚体飞行器转动轴的单位矢量,ei为e的方向余弦,θ为刚体飞行器绕转动轴转动的角度,则有
(1)
设σ=[σ1σ2σ3]T,采用修正Rodrigues参数σ描述刚体飞行器姿态运动学方程为:

(2)
式中
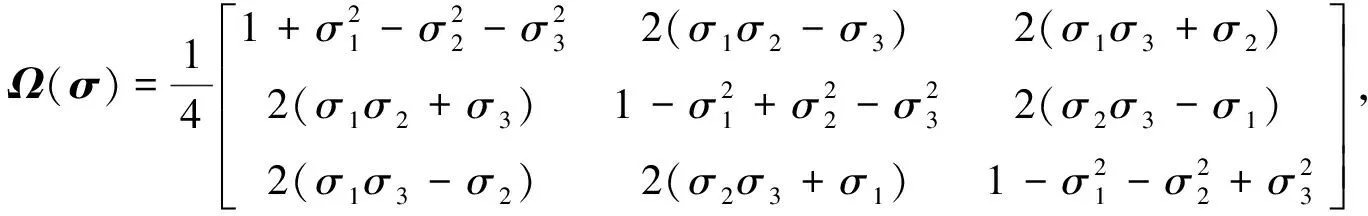
ω=[ωxωyωz]T为刚体飞行器绕转动轴转动的角速度.
考虑刚体飞行器的动力学方程:
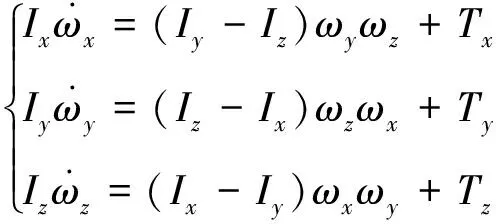
(3)
式中,Ii(i=x,y,z)表示绕星体坐标系第i个主轴的转动惯量,Ti(i=x,y,z)表示绕第i个主轴的控制力矩.
联立式(2)、(3),可得
(4)
式中
f1=[(Iy-Iz)/Ix]ωyωz,f2=[(Iz-Ix)/Iy]ωzωx,
f3=[(Ix-Iy)/Iz]ωxωy,
定义含有角速度和修正Rodrigues参数的状态向量x(t)=[ωxωyωzσ1σ2σ3]T,控制向量u(t)=[TxTyTz]T,则式(4)可改写为LPV系统的形式,即
(5)
式中
a12=[(Iy-Iz)/Ix]ωz,a23=[(Iz-Ix)/Iy]ωx,
设存在状态反馈控制器
u(t)=K(x(t))x(t)
(6)
其中K(x(t))为待定的多项式增益矩阵,则相应的闭环系统为
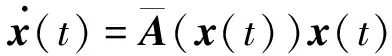
(7)
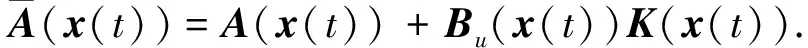
定义与系统状态x(t)和控制输入u(t)相关的性能指标
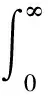
(8)
式中Q=QT>0,R=RT>0为给定的加权矩阵.
本文研究的问题是:对于由式(5)描述的LPV系统,要求设计状态反馈控制器(6),使得相应的闭环系统(7)是稳定的,且由式(8)定义的系统性能指标满足J≤J*,其中J*是某个确定的常数.
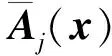
2 控制器优化设计
2.1 平方和分解
定义1.对于n元实系数多项式f(x1,x2,…,xn),若存在一组多项式f1(x),f2(x),…,fm(x),使得
(9)
则称f(x1,x2,…,xn)为平方和(SOS)多项式.
记∑SOS表示所有平方和多项式的集合.根据定义1可知,若f(x)∈∑SOS,则对于∀x∈Rn,均有f(x)≥0成立.
下述命题结出了简便的判定n元多项式是否为SOS多项式的方法[7].
命题1.设f(x)是一个次数不高于2d的n元多项式,Z(x)是由次数不高于d的单项式组成的列向量,则f(x)为SOS多项式的充要条件是存在一个半正定矩阵Q,使得
f(x)=ZT(x)QZ(x)
(10)
下述引理进一步给出了一个判定多项式矩阵是否为半正定矩阵的方法.
引理1[8].设x∈Rn,矩阵F(x)是次数为2d的N×N维对称多项式矩阵,Z(x)是由次数不高于d的单项式组成的列向量,考虑如下3个条件:
(a)对于所有的x∈Rn,均有F(x)≥0;
(b)vTF(x)v是SOS多项式,其中v∈RN是与x不相关的向量;
(c)存在一个半正定矩阵Q,使得vTF(x)v=(v⊗Z(x))TQ(v⊗Z(x)),其中“⊗”表示Kronecker积;
则有:(a) ⟸(b) and (b)⟺(c).
2.2 系统性能分析
引理2.对于对称的非奇异多项式矩阵P(x),有如下关系式成立:
(11)
定理1.如果存在适维对称正定多项式矩阵P(x),使得如下矩阵不等式成立
(12)
其中,
则闭环系统(7)是稳定的,且由式(8)定义的系统性能指标满足
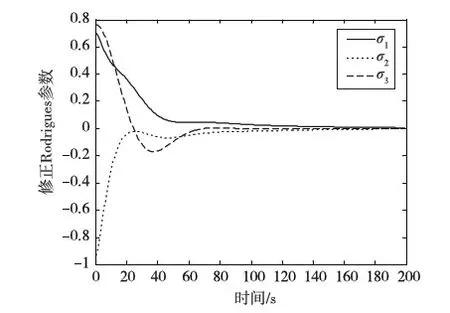
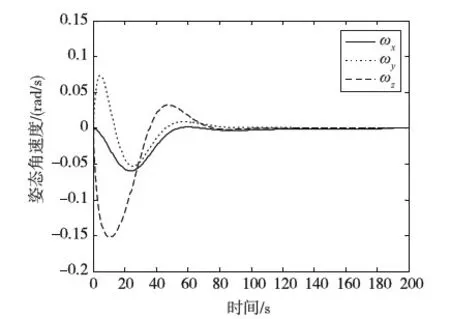
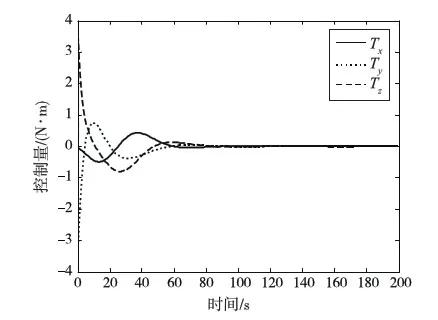
J (13) 证明.选取如下形式的候选Lyapunov函数 V(x)=xTP-1(x)x (14) 由矩阵P(x)的正定性可知,对于任意x≠0,函数V(x)是正定的. 沿闭环系统(7)的任意轨线对V(x)求导,可得 (15) 式中 根据矩阵的Schur补引理,式(12)可表示为 Γ1+P(x)QP(x)+P(x)KT(x)RK(x)P(x)<0 (16) 对式(16)两边分别左乘P-1(x)、右乘P-1(x),并利用引理2,可得 Ω+Q+KT(x)RK(x)<0 (17) 结合式(15)和(17),可得 (18) 进一步的,对式(18)两边对时间t从0到∞积分,并利用系统的稳定性,则有 ≤xT(0)P-1(x(0))x(0) (19) 在定理1的基础上,下述定理以SOS的形式,给出了一个判定LPV系统性能指标(8)的方法. 定理2.如果存在适维对称多项式矩阵P(x),使得 (20) (21) 式中,ε1(x)和ε2(x)为非负多项式,且对于所有的x≠0,ε1(x)>0,ε2(x)>0;v1,v2,v3和v4是与x不相关的向量,则闭环系统(7)是稳定的,且系统的性能指标满足J 证明.结合引理1和定理1可证得该定理. 注1.定理2中的所有条件均以SOS多项式的形式给出,并且能够方便地运用MATLAB平方和优化工具箱SOSTOOLS进行求解[9]. 记J={j1,j2,…,jm}是由矩阵Bu(x)的全零行标志构成的集合,即 (22) 下述定理给出了空间飞行器大角度姿态机动保性能控制器的存在条件和设计方法. (23) (24) (25) 证明.选取如下形式的候选Lyapunov函数 (26) (27) 式中, 令 (28) 并对式(27)进行整理,可得式(24).定理的其余部分容易从前面的分析得到,定理得证. 进一步引入标量λ>0,使得 (29) 根据矩阵的Schur补引理,上式可等价地表示为 (30) 由引理1可知,若式 (31) 成立,则有式(30)成立. 综上可知,状态反馈最优保性能控制器设计可归结为一个具有平方和约束的参数λ最小化问题. 推论1.对于系统(5),若如下优化问题: (32) (33) 且相应闭环系统指标性能的上界是λ*. 以某卫星大角度姿态机动控制为例进行仿真.将卫星的转动惯量矩阵I=diag{100,60,40}(kg·m2)代入飞行器姿态运动方程(5),则运用推论1可设计卫星大角度姿态机动状态反馈最优保性能控制器. 设卫星初始姿态和目标姿态的欧拉角分别为(75°,-175°,70°)和(0°,0°,0°),初始角速度为(0,0,0).根据欧拉角与修正Rodrigues参数之间的关系,可知卫星初始姿态和目标姿态的修正Rodrigues参数分别为(0.7010,-0.9331,0.7624)和(0,0,0). 对于在轨运行的卫星而言,主要控制目标为尽量减少燃料消耗,因而选取加权矩阵Q和R如下: Q=diag{0.1,0.1,0.1,0.5,0.5,0.5},R=diag{1,1,1}. 其中 绕卫星3个主轴的控制力矩分别为 0.00385x1x4+0.0258x1x5-0.1049x1x6- 0.0043x2x4-0.0239x2x5+0.1617x2x6+ 0.09617x3x5+0.0056x3x6+5.4546x3- 0.02842x1x4-0.0335x1x5+0.07189x1x6- 0.1075x2x4+0.05972x5-0.0530x2x6+ 0.0762x3x5-0.0317x3x6-3.81526x3+ 0.0530x1x4-0.1686x1x5+0.1318x1x6- 0.0043x2x4+0.0309x2x5-0.1517x2x6+ 0.1001x3x5-0.0098x3x6+16.0352x3+ 为进一步验证本文设计方法的有效性,对卫星大角度姿态机动控制过程进行仿真.设系统的初始状态为x(0)=[0,0,0,0.7010,-0.9331,0.7624]T,在所设计的状态反馈最优保性能控制器的作用下,描述卫星姿态的修正Rodrigues参数σi(i=1,2,3)和姿态运动角速率ωi(i=x,y,z)随时间的变化曲线如图1和图2所示. 图1 修正Rodrigues参数变化曲线 图2 姿态角速度变化曲线 在卫星姿态机动过程中,绕卫星3个主轴的控制力矩Ti(i=x,y,z)随时间的变化曲线如图3所示. 图3 控制量变化曲线 由仿真结果可以看出,在状态反馈最优保性能控制器的作用下,描述卫星姿态运动的修正的Rodrigues参数能够由初始状态(0.7010,-0.9331,0.7624)达到期望的状态(0,0,0).在卫星姿态机动控制过程中,随着飞行器姿态的变化,施加到卫星3个轴上的控制量逐渐减小,相应的姿态运动角速度也逐渐趋于零. 本文提出了一种基于平方和优化的空间飞行器大角度姿态机动状态反馈最优保性能控制方法.采用修正Rodrigues参数建立飞行器姿态运动数学模型,在此基础上,综合运用Lyapunov方法和平方和优化技术,给出飞行器大角度姿态机动保性能控制器的存在条件和设计方法.对某卫星大角度姿态机动控制的仿真结果表明了所述方法的有效性. 参 考 文 献 [1] Zheng Q, Wu F. NonlinearH∞control design with axisymmetric spacecraft control [J]. Journal of Guidance, Control and Dynamics, 2009, 32(3): 850-858 [2] 马克茂,董志远.空间飞行器大角度机动飞行的变结构姿态控制[J].飞行力学,2004,22(2): 45-48 Ma K M, Dong Z Y. Variable structure attitude control of spacecraft large angle maneuver flight [J]. Flight Dynamics, 2004, 22(6): 45-48 [3] Sharma R, Tewari A. Optimal nonlinear tracking of spacecraft attitude maneuvers [J]. IEEE Transactions on Control Systems Technology, 2004, 12(5): 677-682 [4] Kim K S, Kim Y. Robust back-stepping control for slew maneuvers using nonlinear tracking function [J]. IEEE Transactions on Control Systems Technology, 2005, 13(7): 907-912 [5] Gollu N, Rodrigues L. Control of large angle attitude maneuvers for rigid bodies using sum of squares [C]. The 2007 American Control Conference, New York, USA,July 11-13, 2007 [6] 王佳,曾鸣,苏宝库.基于平方和的卫星大角度姿态机动非线性H∞控制[J].系统工程与电子技术,2010,32(5): 1024-1028 Wang J, Zeng M, Su B K. NonlinearH∞control of large angle attitude maneuvers for satellites using using sum of square [J]. Systems Engineering and Electronics, 2010, 32(5): 1024-1028 [7] Parrilo P A. Structured semidefinite programs and semialgebraic geometry method in robustness and optimization [D]. California Institute of Technology, 2000 [8] Prajna S, Papachristodoulou A, Wu F. Nonlinear control synthesis by sum-of-squares optimization: a Lyapunov-based approach [C]. The 5thAsian Control Conference, Melbourne, Australia,July 20-23, 2004 [9] Prajna S, Papachristodoulou A, Parrilo P A. Introducing SOSTOOLS: a general purpose sum of squares programming solver [C]. The IEEE Conference on Decision and Control, Las Vegas,USA,December 10-13, 2002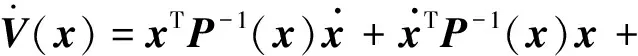
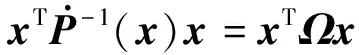

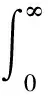
2.3 控制器优化设计
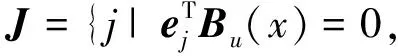


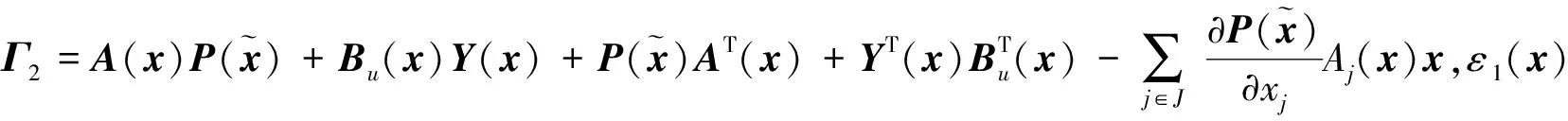
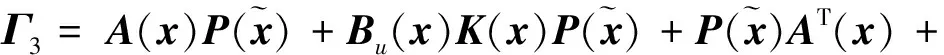
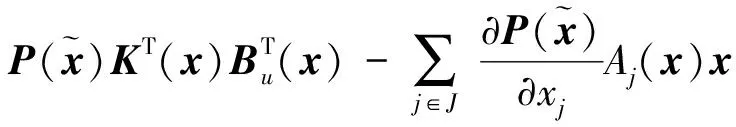
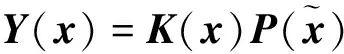
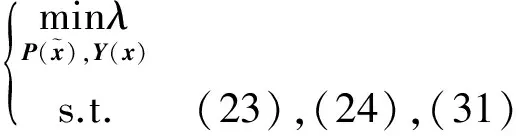
3 算例仿真



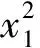
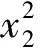
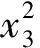
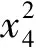
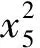
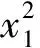
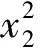
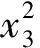
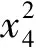
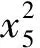
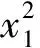
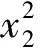
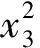
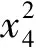
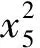
4 结 论
