一种用于阵列测向的多通道幅相误差校正方法
2013-04-26王纯钢
王纯钢
(中国电子科技集团公司51所,上海 201802)
0 引 言
不论是哪种空间谱估计算法都是对信号的复值进行处理,由于进入阵列系统的信号电平比较低,所以进行处理前都需要对接收的信号进行放大和Hilbert变换等一系列的处理。阵列信号处理的物理基础是信号进入接收阵列的各个阵元后,阵元输出的信号之间有严格的相关性。为此,要求信号进入接收阵列系统后,经过放大和Hilbert变换等处理后得到的复信号也有严格的相关性。换句话说,要求从阵列接收系统阵元的感应到复信号输出的整个过程中,阵列接收系统的各通道要有严格的相关性。否则,阵列接收系统的各阵元输出的复信号与信号源到达各阵元的信号复数形式不一样,从而引起最终谱估计有较大的误差,甚至失效。
造成阵列接收系统的各个通道不一致性的因素有:
(1)阵列接收通道的放大和变换使其输出的幅度和相位不一致。其中,影响最大的是本振信号的不一致。
(2)阵列接收系统各个阵元之间的互耦效应。它不仅影响各个阵元感应电压的幅度和相位,也影响各个阵元的输入阻抗。而且,这种影响和信号源的频率有密切的关系。
(3)馈线的长度效应与接收机输入阻抗的不一致性。它也与频率有密切的关系。
(4)接收阵元物理位置和结构的不一致性。它们也是频率的函数。
通道的不一致性可以分为2类:一类是在整个观察时间内,各个通道保持不变,称为慢不一致性;另一类是在整个观察期间中,在一次取样时间内增益和相位保持不变,而在不同的取样周期中,其不一致性发生变化,称为快不一致性。它们均会对阵列测向的精度产生很大的影响。第1类通常都有办法消除或减少它的影响;快不一致性通常是随机变化的,很难消除它的影响。本文主要研究通道慢不一致性的影响和解决方法。
1 对阵列各通道不一致性的校正[1]
1.1 信号模型及问题的描述
设待校正的阵列由N个无方向性的阵元构成,阵列结构形式为线阵。空间有M个远场校正信号源,某一时刻只有一个工作,即它们分时工作。这M个校正信号源的绝对方向角可以不知道,但这M个信号方向之间的角度差必须精确已知。
假定以待校正阵列第1个阵元为坐标原点,以第1个信号源方向为Y轴方向(未精确已知),建立一笛卡尔坐标系。待校正阵列在此坐标系下的坐标设为 (x1,y1),··,(xN,yN)。
当待校正阵列无增益和相位不一致性时,该阵列的流形为:
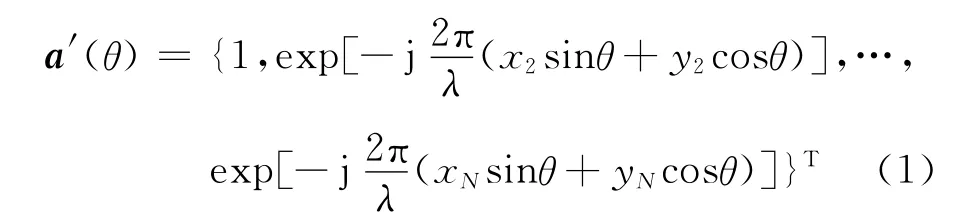
当校正阵列存在增益和相位不一致性时,该阵列的流形为:
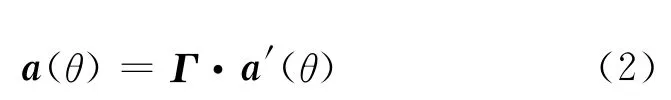
式 中:Γ= diag[ρ1exp(jφ1),ρ2exp(jφ2),…,ρNexp(jφN)],ρi为第i个阵元的增益,φi为第i个阵元的相位。
以待校正阵列的第一阵元通道作为相位和增益的基准,即ρ1=1、φ1=0时,阵列接收到的数据为:
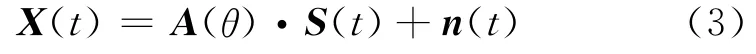
式中:X(t)=[x1(t),x2(t),··,xN(t)]T;A(θ)=[a(θ1),a(θ2),··,a(θp)];S(t)= [s1(t),s2(t),··,sp(t)]T,si(t)为空间第i个信号的复包络;n(t)=[n1(t),n2(t),··,nN(t)]T,ni(t)为第i个阵元的观测噪声,为各自独立的白噪声,且与信号不相关;p为观测时工作信号源数目。
在上述坐标系中,可以假定M个校正信号源与Y轴的夹角为θ1,θ2,…,θM,精确已知,而且θ1=0°,在分时工作时,可以得到M个协方差矩阵:
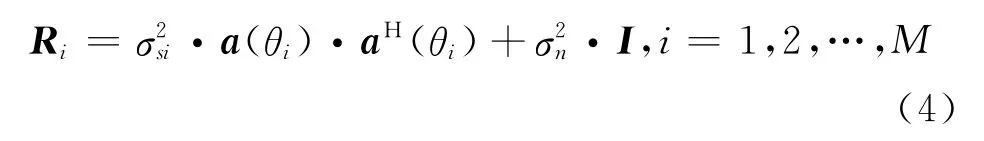
式中:σ2si为第i个校正信号的功率;σ2n为噪声信号的功率。
显然,式(4)右边第1项为秩等于1的矩阵。因此,如果对Ri进行特征分解,其最大特征值所对应的归一化特征向量为V(i)(根据原向量的第1个元素进行归一化),且V(i)=a(θi)。这样,就可以求得待校正阵列的阵列参数。
1.2 阵列参数的求取
首先,用下式来估计Ri:
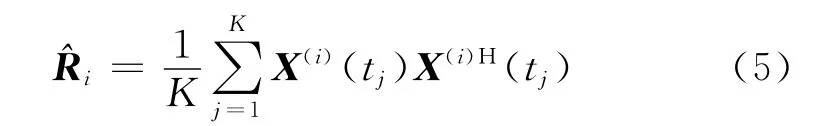
式中:K为采样总数;X(i)(t)为信号源i工作时阵列接收到的数据。
因为进行阵列校正时,一般信噪比较高,且K足够大,可假设:
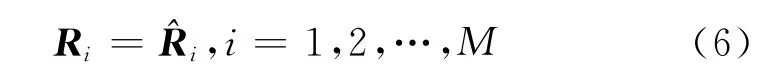
对其作特征分解,可得其最大特征值所对应的归一化特征向量:
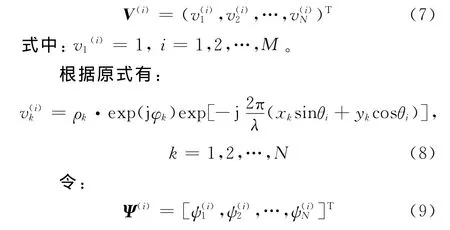
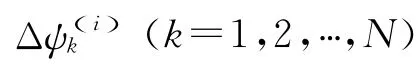
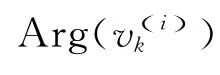
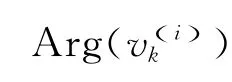
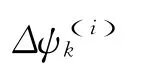

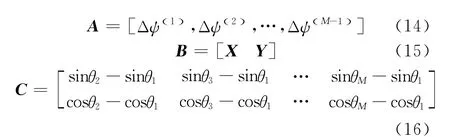
式中:Ψ(i)为测量值;θi为已知值。
只要 Rank(C)=2,就可解得X、Y。显然,Rank(C)=2的条件很容易满足。当M=3时,上述方程有唯一解,当M>3时,上述方程为超定方程,其最小二乘解为:B=A·C+,其中,C+为C的Moore-Penrose广义逆,C+=CT·(C·CT)-1。阵元的位置由下式估计:
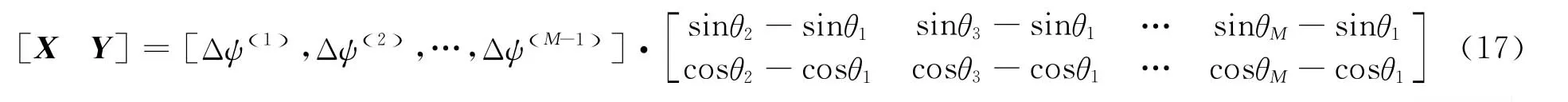
将上式代回到原式,可由下式估计出阵元的相位:
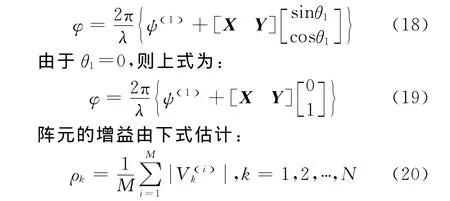
由以上3式,就可以全部估计出阵列的参数。
1.3 阵列增益和相位不一致性的校正
由上面得到了产生干扰的通道参数,根据:
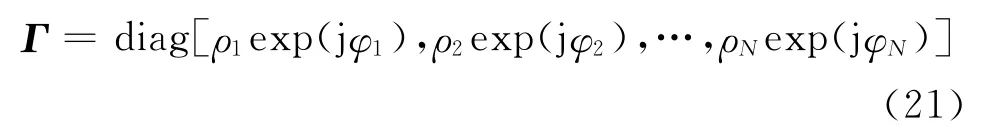
可以很容易求出Γ,然后再利用Γ-1去左乘以X矩阵,即:X′=Γ-1·X,便可以消除通道不一致性对信号的干扰。接下来利用校正后的X′矩阵进行空间谱估计测向,得到的结果便是正确的。
2 仿真试验
有3个待测信号,其方向到达角度分别为30°、-27 °和 -30 °,工 作 频 率 分 别 为 3.995GHz、3.98GHz和3.95GHz,待测量信号的信噪比 为10dB,阵元数为6,阵元间距离按大于最高工作频率4GHz的半波长设计,采样率为500MHz,通道增益偏差为[1,1.3,0.7,1.1,1.2,0.8],通道相位偏差为[0.0,1.4,-0.6,0.1,-0.4,-0.64],通过校正后的对待测信号的估计结果如下:
时空二维空间谱分析的立体图如图1所示。
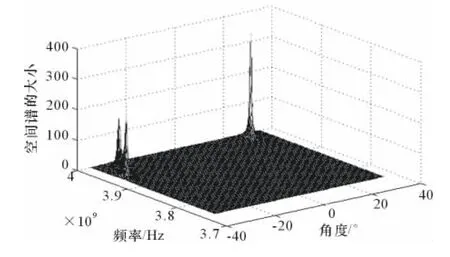
图1 时空二维空间谱分析的立体图
单次估计结果如下:
辐射源方位值:30,-27,-30;
辐 射 源 方 位 估 计 值:3.004 0e+001,-2.740 7e+001,-2.955 3e+001;
辐射源频率值:3.995 0e+009,3.980 0e+009,3.950 0e+009;
辐 射 源 频 率 估 计 值:3.992 6e+009,3.977 1e+009,3.954 5e+009。
30次统计平均结果时空二维空间谱分析的立体图见图2。多次估计统计分析图如图3所示。
30次统计平均估计结果如下:
辐射源方位值:30,-27,-30;
辐射源方位估计值:3.001 3e+001,-2.745 0e+001,-2.968 1e+001;
辐射源频率值:3.995 0e+009,3.980 0e+009,3.950 0e+009;
辐射源频率估计值:3.993 6e+009,3.976 0e+009,3.952 2e+009。
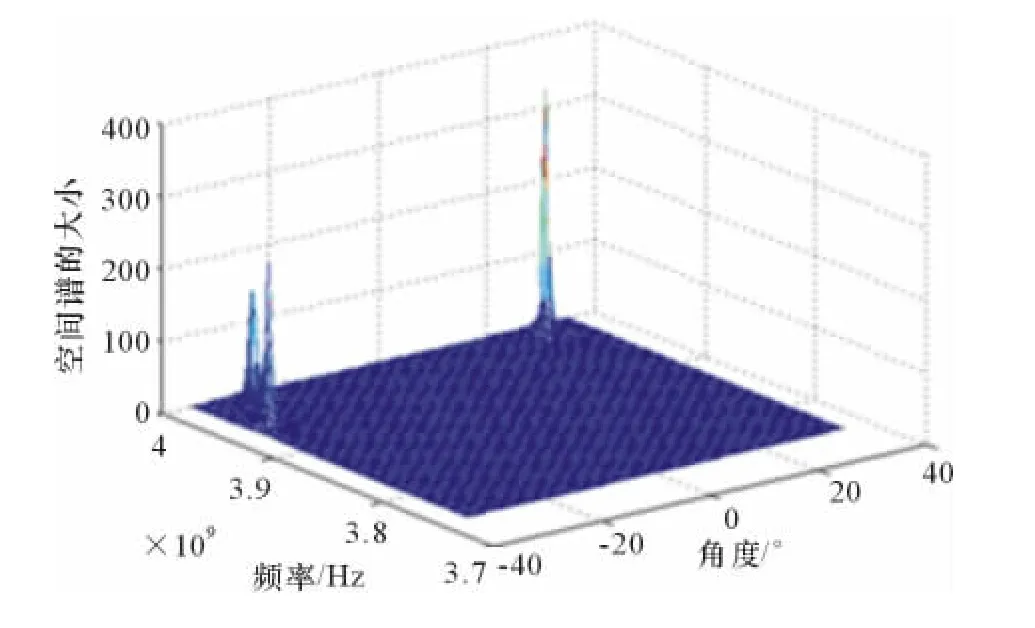
图2 30次统计平均结果时空二维空间谱分析的立体图
3 结束语
本文描述的误差校正方法是基于以下假定:虽然校正源相对于阵元的方向并不知道,但各校正源的波达方向之间的角度差是准确已知的,该方法可以精确地估计出通道的幅相误差。在校正源相对于阵列的波达方向未知情况下,已经证明了线性等距阵列的等距误差不可能完全校正[2-3]。尽管如此,采用此校正方法还是可以通过对阵列的增益和相位的不一致性进行校正,得到较好的辐射源方位、频率估计精度,事实上,通过工程样机的验证,采用一点源校正便已能得到较好的谱估计精度。
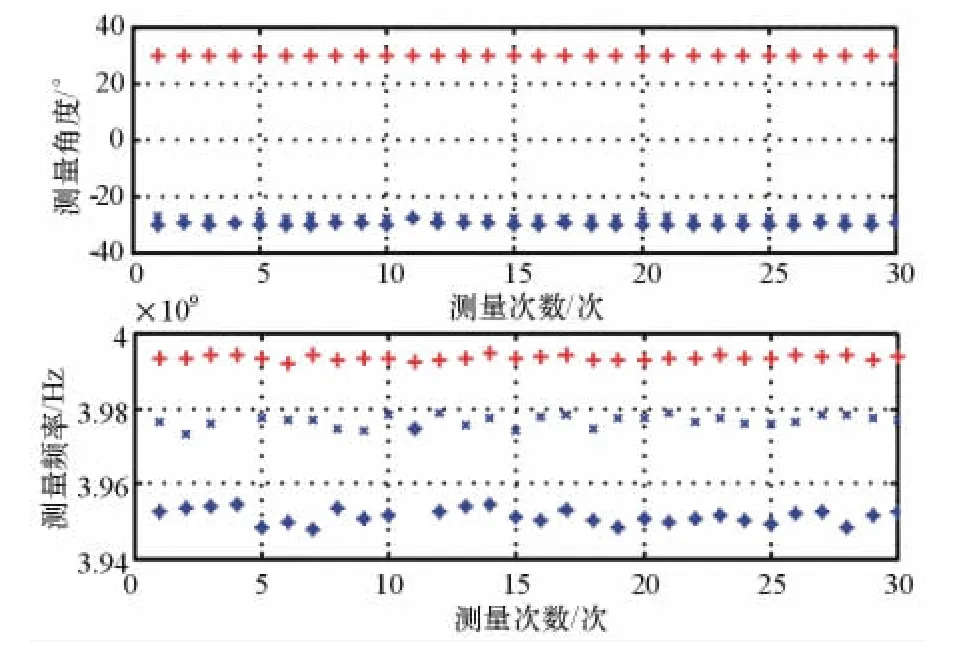
图3 多次估计统计分析图
[1] 刘德树,罗景青,张剑云.空间谱估计及其应用[M].合肥:中国科学技术大学出版社,1997.
[2] Weiss A J,Friedlander B.Eigenstructure methods for direction finding with sensor gain and phase uncertainties[J].Circuits Systems Signal Process,1990,9(3):27-30.
[3] Rockah Y,Schultheiss P M.Array shape caliberation using sources in unknown locations-Part I:far-field sources[J].IEEE Transactions on ASSP,1987,35(3):286-299.
