平面近场测量中截断误差对口径场的不确定性分析

陈玉林，于 丁

(1.华东电子工程研究所 微波技术部，安徽 合肥230031;2.西安电子科技大学 天线与电磁散射研究所，陕西 西安710071)

平面近场测量中，近远场变换理论是基于所有辐射能量均被采集了的假设，所以理论上要采集到天线阵面前无穷大平面的能量。但在实际测量中只能在一个有限的平面上进行采样，而在傅里叶变换(IFFT)中同样是将扫面面以外的近场数据设置为零，这必然会在近远场变换以及天线“诊断”技术中带来误差［4－2］。关于截断误差对天线远场方向图的误差影响国内已有文献［3～4］对此进行研究，但其对口径场的误差影响国内暂时没有此方面的报道。因此，关于这方面的研究无论在理论上还是实际中均有重要意义。

1 截断误差引起的口径场误差表达式

1.1 近场到口径场的解析式

为简化理论推导，假设作近场扫描测量所用探头为理想电偶极子，如图1所示，其位于z=d的平面上。

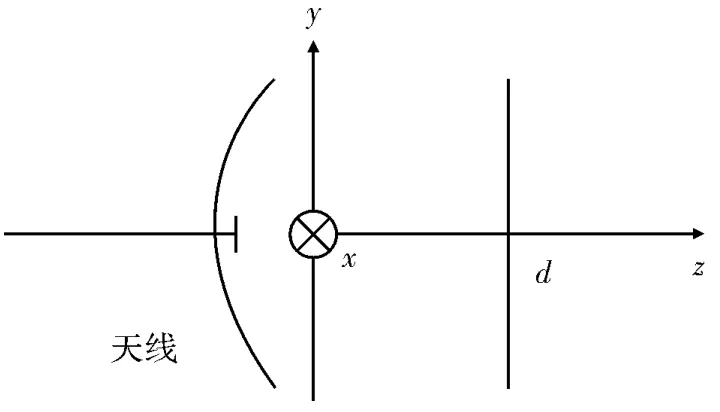
图1 近场扫描测量

则天线的平面波谱At(kx，ky)与采集到的近场横向分量Et(x，y，d)之间的关系为

因为求口径场实际即为d=0处的横向电场，并且考虑只需要得到口径场幅度相位的相对值，在这里略去常数因子。即口径场Et(x，y，0)为

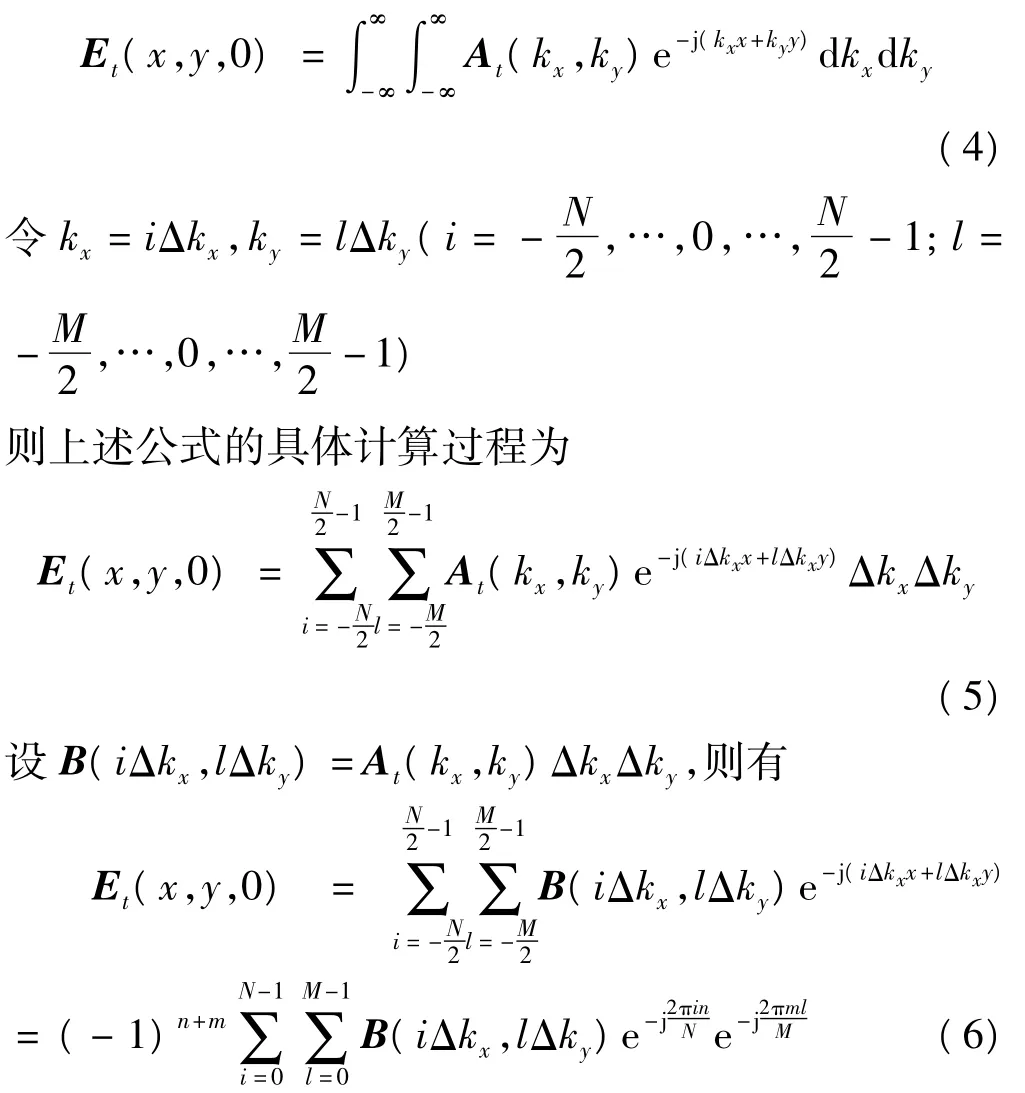
在近场到口径场的变换过程中，考虑到有限面截断的问题，需要将有限扫描面外的场设为零。

1.2 口径场误差表达式

设近场测量中实际扫描面为A0，其互补面积为A1。对近场能量的截断实际为对空间内波谱能量的截断［5］。则由有限截断面引起的横向波谱误差分量ΔAt(kx，ky)为

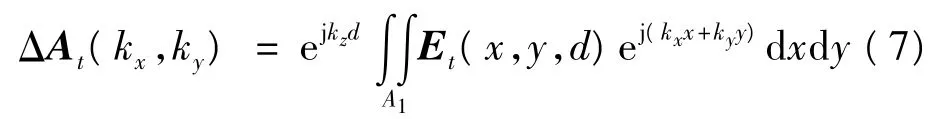
实际测得的波谱分量为

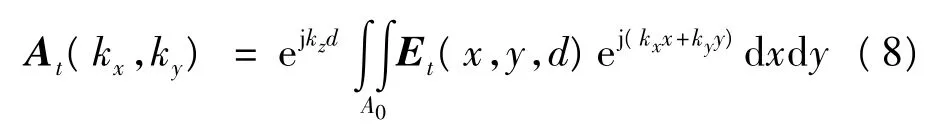
那么由截断误差所造成的口径场误差ΔEt(x，y，0)为

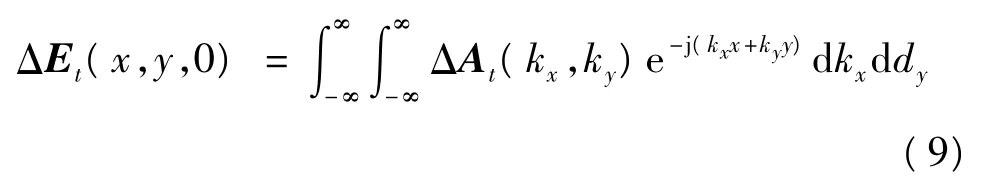
同理，口径场误差的相对分量δ同样为

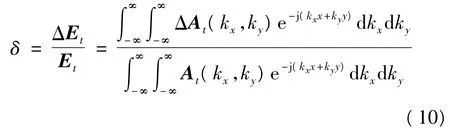
2 截断误差的计算机模拟

为能清楚地反映截断误差对口径场的影响，这里构造以半波对称阵子为单元的天线阵列进行建模分析。

如图2所示，半波振子沿y方向放置，整个阵面沿x方向和y方向分别有2Nx+1，2Ny+1个单元，单元之间的间距分别为dx，dy。采样面到天线阵面的距离为d。阵中单元的电流幅度分布沿x和y皆为余弦分布，记为

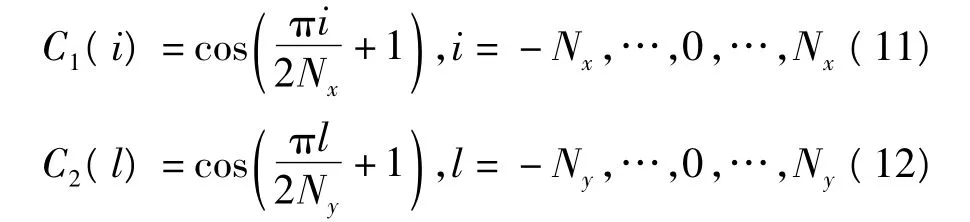
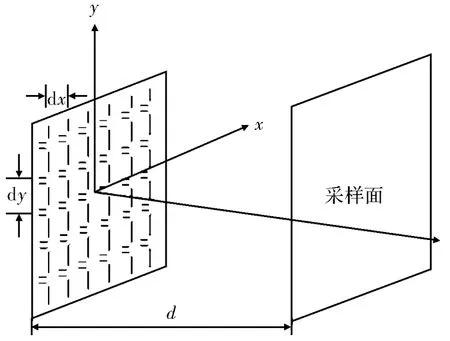
图2 天线阵列建模

电流相位沿x和y方向分别为βx和βy。那么整个阵列在(x，y，d)处产生场的x分量Et(x，y，d)为［5］

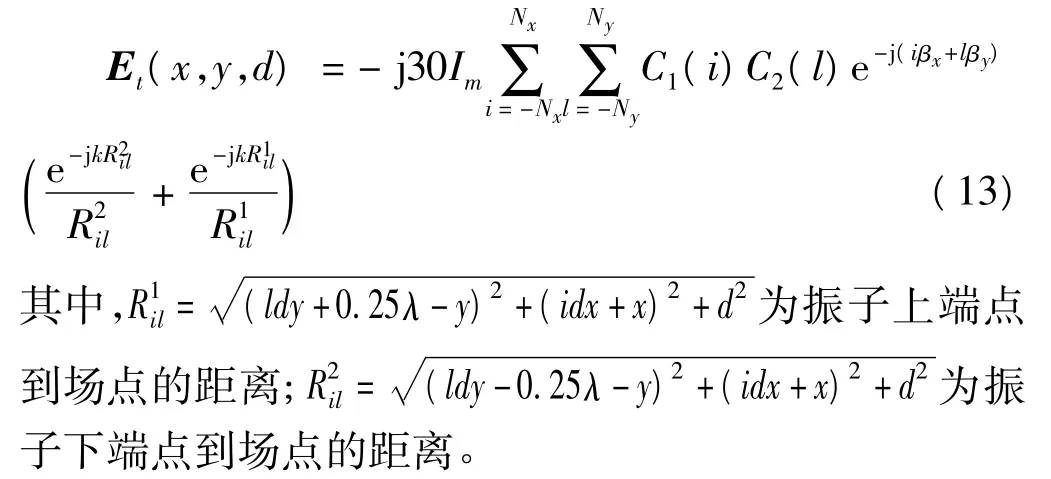
这里取Nx=21，Ny=15，dx=dy=0.7λ，d=4λ，单元电流的相差分别取βx=βy=0。近场采样间隔Δx=Δy=0.45λ，近场采样范围S=l+2d tanθ，θ为截断角，l为天线的最大尺寸。先由式(10)算出天线阵理论的近场数据，然后用傅里叶变换得到天线阵的口径场分布，并变换不同的截断角来分析截断误差对口径场的影响。这里分别取截断角θ=65°;θ=55°;θ=45°的情况与理论口径场进行比较。限于篇幅，这里只给出水平面的口径场幅相分布图，如图3所示。

由图3可知，当取得截断角足够大(θ=65°时)，通过傅里叶变换得到的口径场与原始口径场分布基本一致。而随着截断角的变小，口径场的幅度与相位与原始口径场幅度和相位差别越来越大。可见，在考虑多路径反射的前提下，要选择足够大的截断角，以采得足够的能量，从而得到真实的口径场来更好地“诊断”天线。

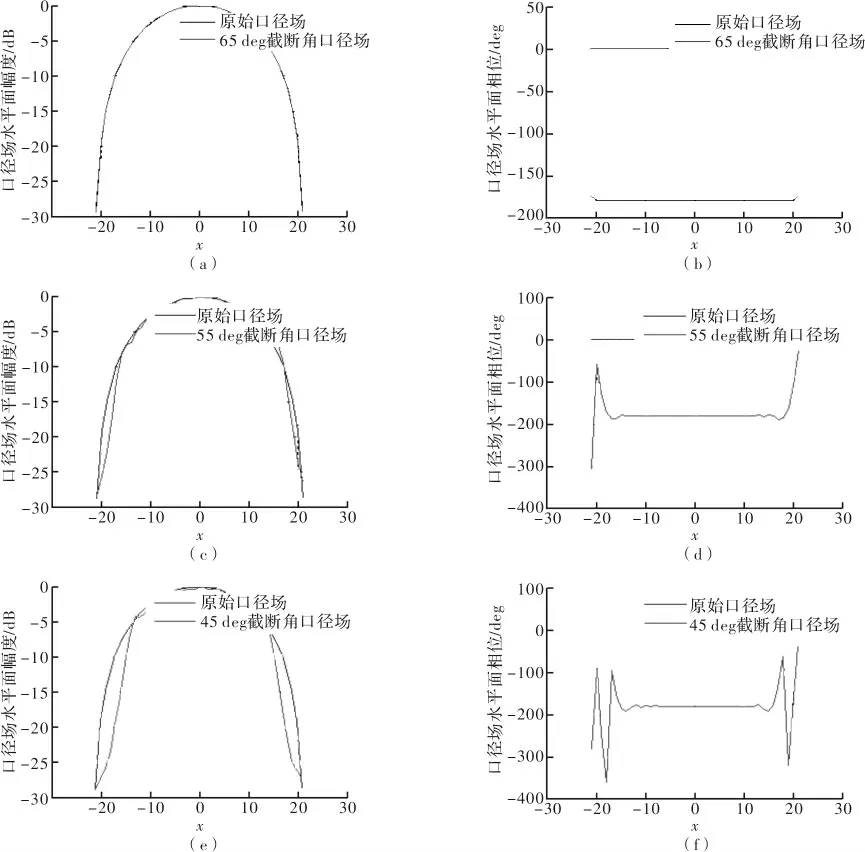
图3 不同截断角口径场幅相与理论口径场幅相比较图

3 结束语

给出了简单的口径场误差表示式，并用计算机模拟的方式分析了不同截断角对天线口径场分布的影响。结果表明，随着截断角的变小，截断能量给口径场带来的误差越来越大。所以，截断误差是近场测试中较大的一项误差源，在实际测试中，要选择适合的截断角，才能采集到足够的能量。

［1］ENRICA M，OLAV B，STEFANO M.Reduction of truncation errors in planar near－field aperture antenna measurements using the gerchberg－papoulis algorithm［J］.IEEE Transactions on Antennas and Propagation，2008，56(11):3485－3493.

［2］ALLENC N.Error analysis techniques for planar near－field measurements［J］.IEEE Transactions on Antennas and Propagation，1988，36(6):754－768.

［3］ 张士选，张进民，方福仂，等.平面近场扫描截断误差分析［J］.西安:西安电 子科技大 学学报，1999，26(4):525－528.

［4］ 于丁，傅德民，刘其中，等.超低副瓣天线平面近场测量截断误差分析［J］.西安:西安电子科技大学学报，2001，28(3):378－382.

［5］ 胡鸿飞.平面近场测量前后变换算法研究及其应用［D］.西安:西安电子科技大学，2000.