粒子群算法支持向量机的半监督回归

马 蕾

(西北工业大学明德学院 计算机信息技术系，陕西 西安710124)

半监督学习理论是近年来模式识别和机器学习中的研究重点和热点，是机器学习方法中介于监督学习和非监督学习之间的新型学习方法。半监督学习的学习样本既包括已标记类别样本也包括未标记类别样本，这样既减轻了标记样本的工作量，又提供了更高效的分类器，从理论和应用角度都具有良好研究意义［1］。半监督学习近年来主要应用于网页检索、文本分类、基于生物特征的身份识别、图像检索、视频检索、医学数据处理等多个实际领域，在回归领域应用并不广泛。常见的半监督学习方法包括:自训练方法(Self Training)、产生式模型(Generative Models)以及对于已有的监督、非监督算法进行修改的半监督学习方法［2］。

粒子群算法(Particle Swarm Optimization，PSO)是近年来发展起来的一种新型进化算法，该算法基于信息共享机制，通过粒子的自我学习和向最佳个体学习的方法来实现对解空间的快速搜索［3］。PSO具有简单、快速收敛、易于实现和精度高等优点。

支持向量机(Support Vector Machine，SVM)是基于统计学习理论的VC维理论和结构风险最小化原则的机器学习技术，根据样本复杂性和学习能力寻求最佳推广能力。SVM在解决小样本、非线性及高维模式识别等问题上都具有显著优势。利用支持向量机解决回归问题，具有泛化能力强、全局最优等明显优势［4］。

本文利用基于粒子群算法支持的向量机建立半监督回归模型。该模型拥有粒子群算法及支持向量机在解决小样本、非线性回归问题上的优势，又集合了半监督学习的优点，适用于解决标记样本不足的情形，有力提高了回归模型的估计精度及模型的泛化能力。

1 遗传算法的支持向量机模型

1.1 支持向量机模型

支持向量机应用于回归问题的数学描述为［5］:给定样本数据(xi，yi)，i=1，2，…，N，其中xi为输入向量;yi为相对应的输出变量;y=f(x)为估计输出量。则被估计函数可表示为

y=f(x)=ωTφ(x)+b

其中，φ(x)为从输入空间到高维空间的非线性映射;ωT为权向量;b为偏置。回归的目标是为了求系数ωT和b，使回归风险函数最小化。回归风险函数为

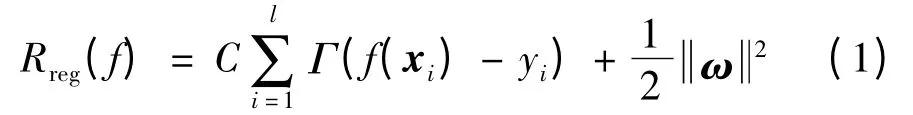
其中，Γ(·)是损失函数;常数C＞0，表示对估计偏差的惩罚度。最常用的损失函数是Vapnik提出的ε不敏感损失函数，形式如下

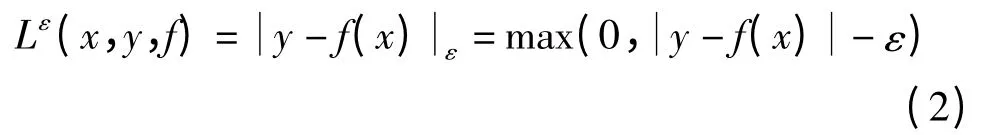
其中，ε不敏感损失函数表示如果预测值与实际值之间的差别＜ε，则损失等于0。

支持向量机在解决回归问题时，是在n维特征空间中，使用ε不敏感度损失函数来求解一个线性回归问题。同时，它要通过最小化来减小模型容量，以保证更好地拟合一般性。于是支持向量机回归，可转化为求解这样一个优化问题［6］

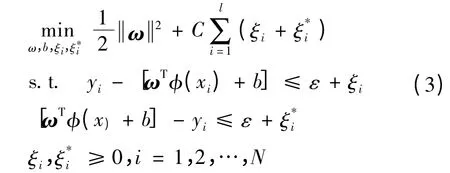
其中，φ为非线性映射函数;ξ和ξ*分别代表在误差ε约束下目标值上下限的松弛变量;C是一个常数，控制对错分样本的惩罚程度。通过拉格郎日优化方法推导可得到其对偶优化问题［7］

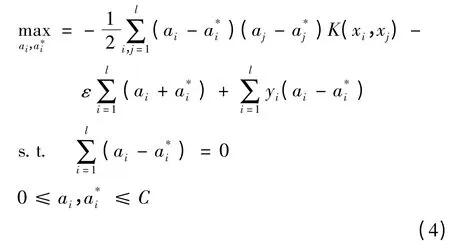
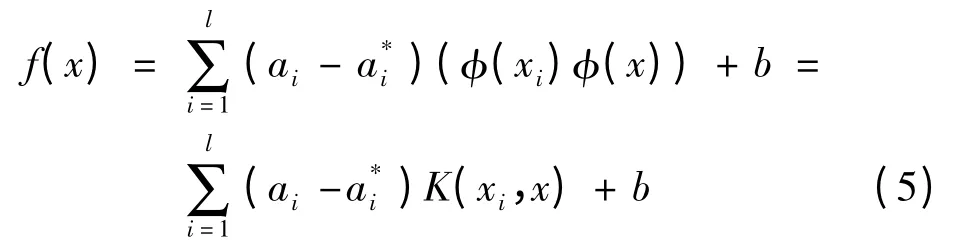
根据Hilbert－Schmidt原理，点积运算可以用满足Mercer条件的核函数K(xi，x)代替。核函数能在不知道变换φ具体函数的情况下，使用低维空间的数据输入来计算高维特征空间中的点积［2］。

在支持向量机回归模型中，包含两个重要的模型参数，即惩罚系数C和核函数的参数，不敏感损失函数ε。其中，C用于控制模型复杂度和逼近误差的折中，C越大，对训练样本数据的拟合程度越高;不敏感损失函数ε的大小决定了支持向量的个数。因此，需要选用适当的智能优化算法来选取合适模型的参数。遗传算法(GA)就是最常见的智能优化算法之一。

1.2 遗传算法的支持向量机模型

遗传算法(Genetic Algorithm，GA)［8］，是一种通过模拟自然进化过程搜索最优解的方法。借鉴了生物遗传学的理论，结合了适者生存和随机信息交换的思想，借助遗传学的遗传算子进行交叉、变异，进而实现种群进化。遗传算法在找寻最优解的过程中，首先在解空间随机产生多个起始点，并同时展开搜索，通过适应度函数来指导搜索的方向，是解决搜索问题的一种通用算法。将遗传算法应用于支持向量机的参数选择，基本步骤如下:

begin

(1)t=0;(2)随机选择初始种群P(t);(3)计算个体适应度函数值F(t);(4)若种群中最优个体所对应的适应度函数值足够大或者算法已连续运行多代，且个体的最佳适应度无明显改进则转到第(8)步;(5)t=t+1;(6)应用选择算子法从P(t－1)中选择P(t);(7)对P(t)进行交叉、变异操作，之后转到第(3)步;(8)给出最佳的核函数参数和惩罚因子C，并用其训练数据集以获得全局最优分类面。

end

其中，适应度函数通常为

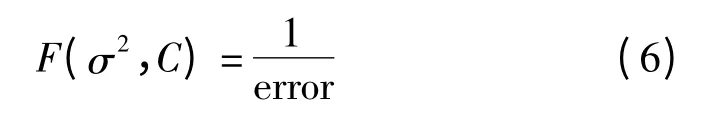
式中，σ2和C是支持向量机中的两个重要参数，核参数和惩罚因子;F(σ2，C)为遗传算法中的适应度函数;Error是SVM在训练样本集上的错分率，可见当SVM在测试样本集上的分类错误率越低时，对应于该组参数的染色体适应度值越大。

2 支持向量机的半监督回归模型

粒子群算法作为一种进化算法，与遗传算法类似，也是从随机解出发，通过不断迭代寻找最优解。但遗传算法并没有采用复杂的交叉、变异过程，而是基于信息共享机制，通过追随当前学习的最优值来寻找全局最优解，实现对解空间的快速搜索［9］。利用粒子群算法选择支持向量机参数，相比基于遗传算法的支持向量机，具有实现简单、快速收敛、调节参数少、精度高等优点。

粒子群算法支持向量机的半监督回归模型(PSOSemi)，以基于粒子群算法的支持向量机回归模型(PSO－SVM)为基础，将未标记样本数据，引入粒子优化过程，回归结果有明显改进。利用粒子群算法支持向量机的半监督模型(PSO－Semi)回归的步骤如下［10］:

(1)读入样本集，并对样本集进行预处理。

(3)计算每个粒子的适应度。利用已标记样本集(XL，YL)训练SVM模型，并对未标记样本数据(x∈Xu)做回归，得到未标记样本集的标记结果集Yu，将未标记样本集Xu及其回归结果集Yu分别加入已标记样本集(XL，YL)。此时，重新训练SVM模型，而后对测试样本做回归，计算每个粒子的适应度，取适应度函数为

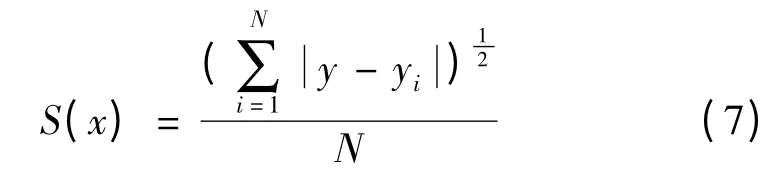
其中，yi为第i个样本的实测值;y为第i个样本的预测值;i=1，2，…，N，N为测试样本个数。

(4)比较适应度，确定每个粒子的个体极值点

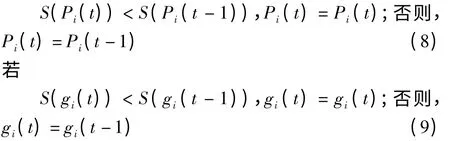
其中，S(x)为适应度函数;Pi为第i个粒子的个体最优值;gi为全局最优值。

(5)更新每个粒子的位置和速度。根据公式

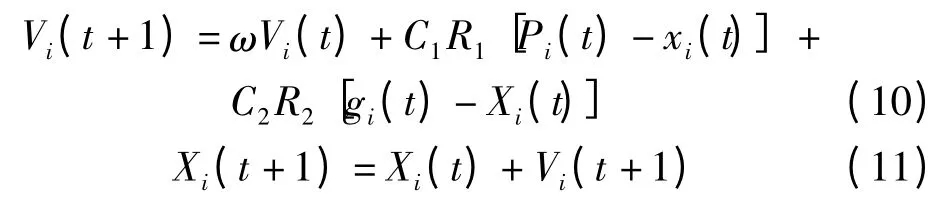
式中，Xi=(Xi1，Xi2，…，Xid)表示第i个粒子在d维空间的位置;Vi=(Vi1，Vi2，…，Vid)表示第i个粒子的速度，它决定粒子在搜索空间单位迭代次数的位移;d为实际解决问题中的自变量个数;ω表示惯性权重;C1和C2是加速常数;R1和R2表示在［0，1］区间的随机数。其中，惯性权重ω对优化性能有明显作用，ω较大，有利于避免局部最小，相反则有利于算法收敛。而加速常数C1和C2代表粒子群之间的信息交流，选择合适的加速常数，既可以加快收敛，又保证了算法不易出现局部最优。根据Shi和Eberhartl对平衡随机因素的研究［11］，可以将加速常数取为2，惯性权重ω设置为0.9～0.4的线性下降。分别更新粒子的速度和位置，并且考虑更新后的速度和位置是否在限定的范围内。

(6)比较次数是否达到最大迭代次数，若满足则停止迭代，得到测试样本的回归结果;否则返回步骤(3)，算法继续迭代。

3 实验方法及结果分析

文中采用均方误差值(Mean Squared Error，MSE)以及可决系数R2来评价实验的回归结果，其中MSE的计算公式为

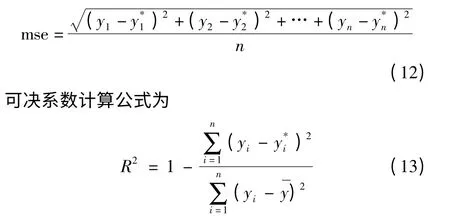
其中，y1，y2，…，yn是测试数据的真实值;是回归模型对测试数据的估计值。MSE反映了估计值与真实值之间差异程度。可决系数R2反映了模型的拟合程度，R2在(0，1)区间取值，越接近1，拟合度越高。实验中，针对实验数据集，分别使用基于遗传算法支持向量机回归模型(GA－SVM)，基于粒子群算法的支持向量机回归模型(PSO－SVM)，以及粒子群算法支持向量机的半监督回归模型(PSO－Semi)等3种模型，求得实验数据的均方误差值MSE和可决系数R2，并对实验结果进行了分析比较。

3.1 实验数据集

实验采用5组常见回归测试数据集［12］，如表1所示。

表1 实验数据集

针对半监督学习适用于缺少或难以获得已标记样本的情况，实验中，只采用10个在取值范围内均匀分布的已标记样本，30个未标记样本和20个测试样本。并对样本值及目标值进行了归一化处理。利用上述3种模型对测试数据集的测试结果的均方误差值MSE和可决系数R2，分别如表2和表3所示。

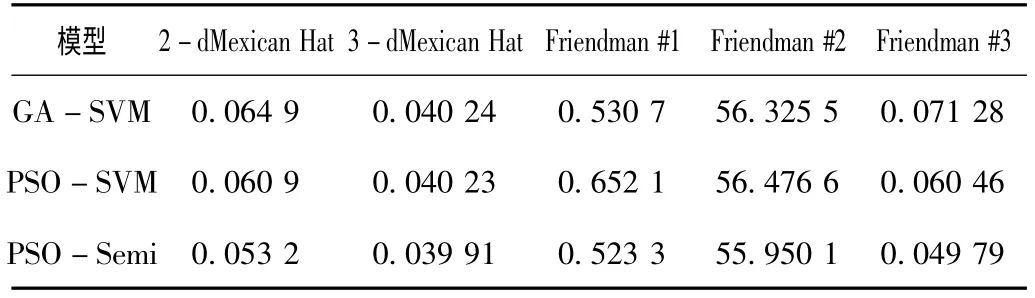
表2 3种模型在数据集上的均方误差值结果

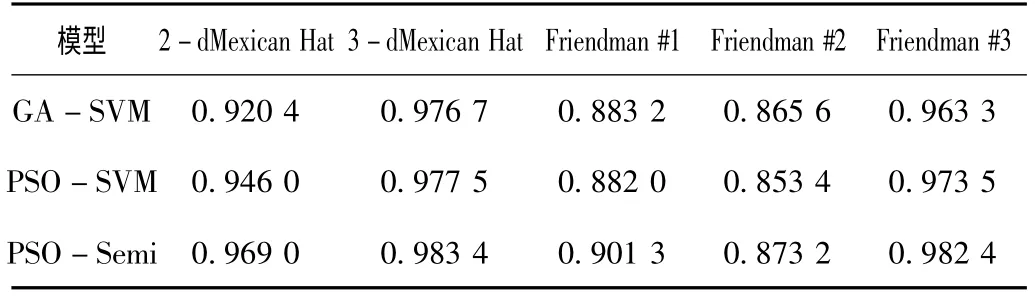
表3 3种模型在数据集上的可决系数

3.2 结果分析

根据表2和表3所示的实验结果，将3种模型分别应用于2－dMexican Hat，3－dMexican Hat，Friendman #1，Friendman #2，Friendman #3等5组数据集上，可以看出，粒子群算法支持向量机的半监督协同回归模型PSO－Semi的均方误差值和可决系数R2两种实验结果都优于其他两种支持向量机模型，切实改善了回归结果，提高了模型拟合度。实验证明，采用半监督学习的回归模型发挥了半监督学习中未标记样本的作用，同时提高了模型的泛化能力，改善了模型的回归精度。另外，由于PSO算法本身具有收敛速度快的特点，PSO－Semi模型的收敛速度与GA－SVM模型相比也具有明显的优势。

4 结束语

提出了粒子群算法支持向量机的半监督回归模型，该模型将粒子群算法支持向量机收敛速度快、精度高等特点与半监督学习的优势相结合，有效地利用了大量的未标记样本，提高了回归估计的精度，在缺少已标记样本的情况下，比基于普通遗传算法和粒子群算法的支持向量机模型有明显的优势。为更加有效地提高回归估计的结果，改进现有的支持向量机半监督回归模型，如使用其他优化算法或采用其他回归模型等，可成为未来研究的方向。

［1］ZHU X J.Semi－supervised learning literature survey［R］.USA MA:University of Wisconsin－Madison，Tech Rep:1530，2005.

［2］ 马蕾，汪西莉.基于支持向量机协同训练的半监督回归［J］.计算机工程与应用，2011，47(3):177－180.

［3］ 任洪娥，霍满冬.基于PSO优化的SVM预测应用研究［J］.计算机应用研究，2009，26(3):867－869.

［4］ 边肇祺，张学工.模式识别［M］.北京:清华大学出版社，2000.

［5］ 张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26(1):32－42.

［6］STEVE R G.Support vector machines for classification and regression［D］.UK Southampton:University of Southampton，1997.

［7］VAPNIK V，LERNER A.Pattern recognition using generalized portrait method［J］.Nauka，Moscow Automation and Remote Control，1963，24(2):774－780.

［8］ 王小平，曹立明.遗传算法理论、应用与软件实现［M］.西安:西安交通大学出版社，2002.

［9］EBERHART R C，KENNEDY J.A new optimizer using particle swarm theory［C］.Newyork USA:Proceedings of the Sixth International Symposium on Micro Machine and Human Science，1995:39－43.

［10］高芳.智能粒子群优化算法研究［D］.哈尔滨:哈尔滨工业大学，2008.

［11］SHI Y H，EBERHART R C.Parameter selection in particle swann optimization［C］.SanDiego:Annual Conference on Evolutionary Programrning，SanDiego，1998.

［12］ZHOU Zhihua，WU Jianxin，TANG Wei.Ensembling neural networks:many could be better than all［J］.Artificial Intelligence，2002，137(1－2):239－263.