中国铁路网的可达性分析

江 娟，肖 宁

（华中科技大学，湖北 武汉 430074）

中国是一个典型的大陆型国家，由于经济联系和交往跨度大，铁路运输系统是一项重要的基础设施系统。它将整个国家联系起来的同时还能引导和促进其它运输方式以及国民经济的发展。铁路运输具有载运量大、运行成本低、安全准时、能源消耗少的特点。在中国交通运输中发挥着其他交通方式不可替代的作用。党的十六大以来，我国的铁路事业进入了全面建设时期，在许多方面取得了显著的成就。

可达性是评估交通网络的一项重要指标。这个概念由Hansen在1959年首次提出，他将网络的可达性定义为网络中的各节点间相互作用的几率大小[1]。多年来，通过不断的引申和发展，可达性的内涵日益丰富。评价它的方法和指标也日益多样，各种方法和指标有着不同的侧重点[2-4]。可达性分析广泛应用于交通领域的相关研究中。Javier Gutikrez在1996年对欧洲铁路网的可达性进行了预测性的分析。他们根据欧洲铁路2010年的规划图，分析了高速铁路的发展对整个铁路网络在时间距离上的可达性的影响，并且分析了铁路的发展对城市格局的影响[5]。同样，2004年金凤君和王娇娥也将运输距离以及通达性系数等作为指标，分析了中国铁路网络的可达性。他们根据中国铁路网可达性的演变，分析了中国铁路的发展历程，将中国铁路网的发展总结为起步、筑网、延伸和优化四个阶段[6]。蒋海兵等以京沪高铁为例，分析了高铁对区域中心城市可达性的影响[7]。Antonio Antunes等提出了将网络可达性最大化的铁路网络规划方法，并将其用于公路网络中验证方法的可行性[8]。2006年Michael A.P.Taylor以公路网为研究对象分析了可达性的下降对网络脆弱性的影响[9]。张莉和靳诚等分别以长江三角洲和南京市区的景点为例，分析了陆路交通网的可达性[10-11]。

复杂网络作为大量真实复杂系统的高度抽象，其理论与应用研究已渗透到数理、生命和工程学科等众多不同的领域。利用复杂网络的理论能够很好地描述铁路系统的内部结构和彼此间的关联关系。但在利用复杂网络理论对铁路网进行分析时大多数只是从网络的结构出发，没有结合铁路网的基本特征。笔者认为，在利用复杂网络理论对实际的复杂系统进行研究时，必须要考虑到实际系统的基本特征。例如，节点在铁路网络中的可达性不仅与网络的结构有关，更与运行于网络之上的列车有些紧密的联系。单从网络的结构出发，研究铁路网络的可达性，存在一定的局限性。鉴于此，本文由铁路网络的特征出发，从网络和功能两个不同的角度分析网络的可达性，更加全面、准确地揭示中国铁路网节点的可达性。

1 研究对象与建模方法

1.1 研究对象

本文以中国铁路网为研究对象，数据主要包含中国铁路网络拓扑结构以及列车时刻表。拓扑网络中节点的选取方法如下：（1）选出所有的客运的火车站点；（2）挑选出位于大城市或者大城市周边的火车站点；（3）挑选出是某一趟列车的起点或者终点的火车站点；（4）位于同一城市中的多个火车站点，将其用一个站点名代替，例如：武汉市有三个火车站，分别为武汉站，武昌站和汉口站，我们将其用一个站点取代：武汉。经过上述方法一共得到400个火车站点以及505条边。同时根据所收集到的人口、GDP数据，在挑出的400个火车站点所处的城市中，包含了中国的人口、GDP数据排名前300的城市和地区。列车时刻表来源于由铁道部运输局于2010年10月出版的全国铁路旅客列车时刻表。列车时刻表中包含4 196趟列车，其中包含编号为字母“G”字头的高速动车组列车322趟；编号为字母“C”字头的城际动车组列车118趟；编号为字母“D”字头的动车组旅客列车731趟；编号为字母“Z”字头的直达特快旅客列车66趟；编号为字母“T”字头的特快旅客列车329趟；编码为字母“K”字头的快速旅客列车1 496趟；编号为“1008-5998”的普通旅客快车834趟；编号为“6001-7598”的普通旅客慢车302趟。

1.2 建模方法

本文中所用到的模型为双层结构模型。根据Maciej Kurant和Patrick Thiran在2006年提出的双层结构模型[12-14]，将模型中逻辑层的意义做一定的改进，是它更适合本文的研究。如图1所示：

GØ称为物理层，表示物理网络，即铁路的拓扑结构。用GØ（VØ, EØ）表示；Gλ称为逻辑层，它的每一条边两端连接的两个节点是能够通过一趟列车直达的两个铁路站点，用 Gλ（Vλ,Eλ）表示，其节点数目与物理层上一致；M（Eλ）称为映射层，它映射了逻辑层上的每一条边在物理层上的实际路径。例如：物理层上线路，其在逻辑上对应于边，边在物理层上的映射为路径，它反应了经过两个铁路站点列车的实际行驶路径。即节点之间有列车直达，列车的行驶路径为。模型中物理层上网络为无向网络；而逻辑层中网络为有向网，方向为两点间列车的行驶方向。

2 可达性分析

本文将从两个不同的角度分析中国铁路网的可达性：铁路网络的拓扑结构以及运行于铁路之上的列车，即模型中的物理层和逻辑层。在两个不同层面上分别定义不同的可达性指标，比较它们的差异，分析指标的有效性。

2.1 物理层可达性分析

物理层上可达性定义为：网络中任意节点i与其它所有节点j≠i之间的最短路径的平均值。即物理层上，任意节点i与其它所有节点j≠i之间边的数量的最小值的平均值。其值越高，表示可达性越差：

其中，dij为节点i,j之间的最短路径，NØ为物理层上节点的数目。

该指标仅从网络的拓扑结构来分析网络的可达性，与节点在网络中的位置以及网络的分布密切相关，但是与列车的行驶路径无关。仅仅是利用复杂网络理论从网络拓扑的角度来分析，未结合铁路网络的基本特征。物理层上中国铁路网的拓扑结构如图2左图所示，其拓扑性质如表1所示，NØ为节点数目，EØ为边的数目，DØ为网络直径，LØ为平均路径长度，（k）Ø为平均度。

根据式（1）计算物理层上400个节点的可达性。其中，可达性排名前20的铁路站点的详细情况如表2所示；它们所处的地域与如图4左图所示。

由图4可以看出，在物理层上可达性较好的节点主要位于中国的中部和东部地区，分布比较集中。排名前20的节点的Pi值均小于网络的平均路径长度。造成这样的原因不仅是因为这些节点所处的位置，更重要的是在这片区域中，铁路站点、铁路线的分布比较密集。但是这20的节点中却不包含北京、上海、郑州等交通枢纽。

2.2 逻辑层可达性分析

逻辑层上可达性定义为：网络中任意节点i到其它所有节点j≠i最少需要乘坐的列车趟数的平均值。即逻辑层上，任意节点i与所有其它节点j≠i之间边的数目的最小值的平均值。其值越高，表示可达性越差：

其中，kij表示节点i到节点j最少需要乘坐的列车趟数，Nλ为物理层上节点的数目。

该指标结合了铁路网的特征，在网络拓扑结构的基础上加入了列车信息，根据列车的行驶路径判断节点的可达性。结合了铁路系统的实际情况。不仅与拓扑结构有关，还与列车的行驶路径相关。逻辑层上中国铁路网的拓扑结构如图2右图所示。其拓扑性质如表1所示，Nλ为节点数目，Eλ为边的数目，Dλ为网络直径，Lλ为平均路径长度，（k）λ为平均度。其节点的数目Nλ与物理层上的节点数目NØ相等。边的数目Eλ为奇数，说明了中国铁路系统中以相同的铁路站点分别为起点或终点的列车，其行驶路径并不是完全对称的。Dλ=6说明铁路网中任意两个铁路站点之间最多需要6趟列车可达。

?

本文中将节点i到节点j需要乘坐的列车趟数kij为一趟、二趟、三趟、四趟及以上的节点对之间的可达类型分别记为类型1、类型2、类型3、类型4。

根据列车时刻表以及网络的拓扑结构计算中国铁路网所有节点对（400×400-400对）之间的可达类型，各种可达类型所占比重如图3所示。

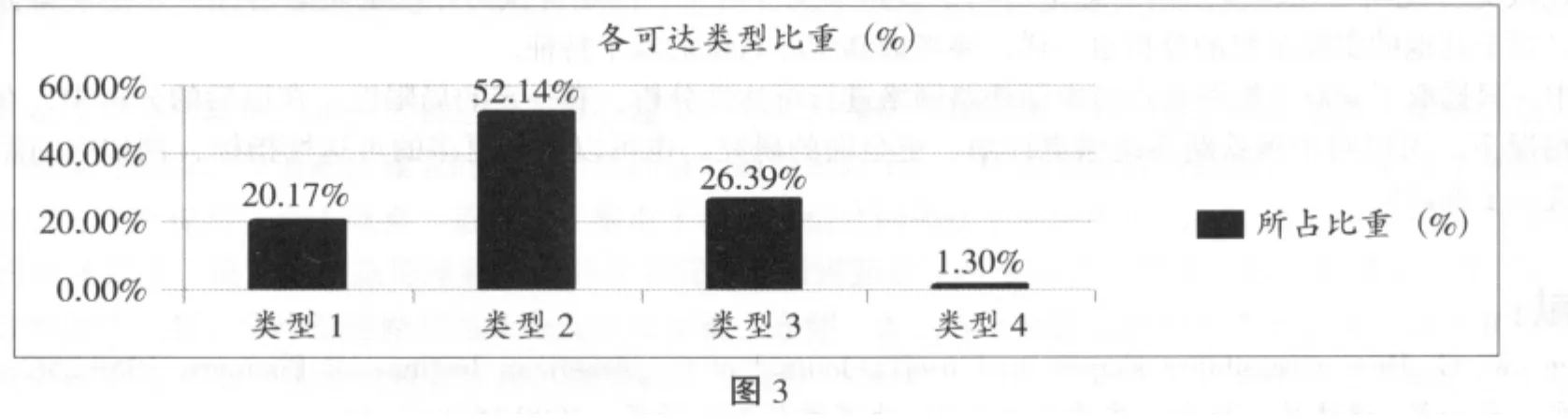
从图3中可以看出，类型4所占比重很小，所以可将两点之间4趟及4趟以上列车可达的节点对归于一类。由图中可以看出，中国铁路客运网中任意两个火车站点之间，大多数可以通过小于等于两趟列车连通，即逻辑层上任意两节点间的最短距离大多数为1和2，小于网络的平均路径长度。最短距离为2的节点对数目最多，超过了节点对总数的一半，高达52.14%。

根据式（2）计算逻辑层上400个节点的可达性。其中，可达性排名前20的铁路站点的详细情况如表2所示；它们所处的地域与如图4右图所示。

由图4可以看出，在逻辑层上可达性较好的节点与物理层上有很大的差异，这20个节点分布的区域比较广，不像物理层上分布比较集中，并且这些节点大部分为省会城市或者直辖市，分布在中国经济比较发达，客流量相对较大的区域。例如北京、上海、武汉、郑州等都是我国比较重要的交通枢纽。排名前20的节点其Li值也均小于逻辑层上网络的平均路径长度。显然，逻辑层上得出的可达性结果比物理层上的结果更为合理。通过比较说明了在利用复杂网络理论对铁路系统进行分析时，结合铁路系统的实际特征分析，得到的结果更为合理，更能反映出铁路网的实际情况。

3 小 结

可达性是评估交通网络的一项重要指标。铁路网络中，节点的可达性不仅与节点在网络中的位置，网络的拓扑结构有关，更加与运行于网络之上的列车息息相关。

本文以中国铁路网为研究对象，利用改进后的双层网络模型，分别从物理层和逻辑层，即铁路网络的拓扑结构以及列车两个不同的角度分析了中国铁路网中节点的可达性。在不同层面上定义了不同的可达性指标，通过计算，两个指标存在着较大的差异。物理层上，可达性较好的节点主要分布在我国的中偏东部，主要原因是由于这些节点所处的位置和这片区域的铁路分布比较密集；逻辑层上，可达性较好的节点分布比较广，不像逻辑层上那样密集，其主要分布在我国客流量较大以及经济比较发达的区域，其中包括北京、上海、武汉、郑州等交通枢纽。显然，在逻辑层上得到的中国铁路网节点的可达性结果更为合理。本文通过比较充分说明了在将复杂网络理论应用于铁路系统分析时，需结合铁路系统的实际特征，才能使得分析结果更加合理、准确。对于其他的实际系统的分析也一样，要考虑到实际系统的基本特征。

本文中，只选取了400个铁路站点对中国铁路网络进行可达性分析，有一定的局限性。在以后的分析中，在有足够的数据做支撑的情况下，可以对中国铁路系统做更详细、更全面的研究。也可以加入更多的可达性指标，例如空间距离、时间距离等，做更进一步的研究。

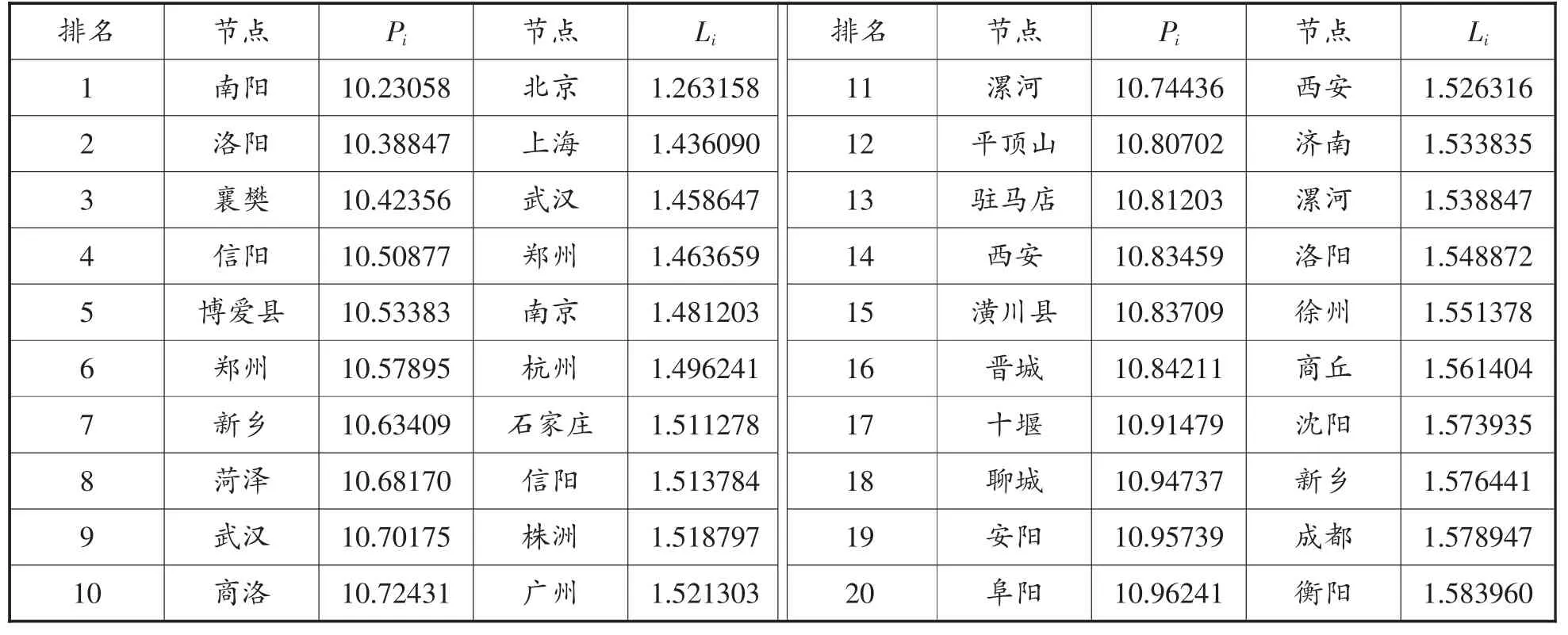
表2 中国铁路网节点的可达性

[1]Hansen,W.G.How accessibility shapes land use[J].Journal of the American Institute of Planners,1959,25(2):73-76.

[2]杨家文，周一星.通达性；概念，度量及应用[J].地理学与国土研究，1999,15(2):61-66.

[3]Van Wee B.,M.Hagoort,et al.Accessibility measures with competition[J].Journal of Transport Geography,2001,9(3):199-208.

[4]Grubesic T.,M.Zook.A ticket to ride:Evolving landscapes of air travel accessibility in the United States[J].Ibid,2007,15(6):417-430.

[5]Gutierrez J.,R.Gonzalez,et al.The European high-speed train network:predicted effects on accessibility patterns[J].Ibid,1996,4(4):227-238.

[6]金凤君，王姣娥.20世纪中国铁路网扩展及其空间通达性[J].地理学报，2004,59(2):293-302.

[7]蒋海兵,徐建刚,等.京沪高铁对区域中心城市陆路可达性影响[J].Ibid,2010,65(10):1287-1298.

[8]Antunes,A.,A.Seco,et al.An accessibility-maximization approach to road network planning[J].Computer-Aided Civil and Infrastructure Engineering,2003,18(3):224-240.

[9]Taylor,M.A.P.,S.V.C.Sekhar,et al.Application of accessibility based methods for vulnerability analysis of strategic road networks[J].Networks and Spatial Economics,2006,6(3):267-291.

[10]张莉，陆玉麒.基于陆路交通网的区域可达性评价——以长江三角洲为例[J].地理学报，2007,61(12):1235-1246.

[11]靳诚，陆玉麒,等.基于路网结构的旅游景点可达性分析——以南京市区为例[J].地理研究，2009(1):246-258.

[12]Kurant M.,P.Thiran.Layered Complex Networks[J].Physical Review Letters,2006,96(13):1-4.

[13]Kurant M.,P.Thiran.Extraction and analysis of traffic and topologies of transportation networks[J].Physical Review E,2006,74(3):1-10.

[14]Kurant M.,P.Thiran,et al.Error and attack tolerance of layered complex networks[J].Ibid,2007,76(2):1-5.