运动着的电离层不均匀体的观测研究
2013-04-23焦培南杨龙泉王世凯
蔚 娜 焦培南 杨龙泉 王世凯 晏 庆
(1.中国电波传播研究所,山东 青岛 266107;2.海军通信应用研究所,北京 100841)
引 言
电离层不均匀性主要包括Es层、扩展F层和电离层行波式扰动[1]. 电离层的不均匀性会严重影响经其传播的电波信号的幅度、相位、群路径等特征参数,反映到探测得到的扫频电离图或定频群距离-多普勒谱图上会出现异常特征,因此,通过对接收到的电波信号的研究就有可能获得反射点电离层的状态信息[2-7].
文献[7]介绍了采用KEL IPS71电离层探测仪观测到的Es层和F2层的“微笑图”(smilergram),这是在某一探测频率上得到的虚高-多普勒谱图上呈现的特殊谱图,造成这种观测结果的主要原因是上空电离层在一个恒定高度上存在着一块匀速水平运动的不均匀体.
在电离层斜向探测试验中,得到的某些探测频率的群距离-多普勒谱图中,也观测到了具有上述相似“微笑”特征的谱图,并且这一现象同时存在于Es层和F2层. 类似的,造成这种现象的原因可能是电离层反射区为一运动着的不均匀体. 基于简单的几何形状,分析了理想情况下的群距离-多普勒谱图特征,并与实测结果进行关联,二者能够很好地吻合,并基于此,估计出了不均匀体的运动速度.
1 理论模型
假设电离层为对称球面电离层,发射站设在A点,接收站设在与发射站相距D的B处,如图 1所示. 假设在反射区存在一块运动着的电离层不均匀体,其具有水平运动速度分量νH和垂直运动速度分量νV.
理想情况下,由A点经电离层反射到B点,电波传播具有最小群距离的反射路径应该是经中点C反射的那条路径,水平运动速度分量不会对该条路径的来波信号产生任何影响,而垂直运动速度分量会使该条路径的来波信号产生一个多普勒频移,因此根据得到的群距离-多普勒谱图,找出某一模式群距离最小值P0对应的多普勒频移fd0,就可以得到反射区不均匀体的垂直运动速度分量νV,即
νV=(cfd0)/(2f),
(1)
式中:c为光速;f为探测频率.
由于收发站地面距离已知,联合测得的P0,则根据式(2)可以计算出反射高度h,
(2)
式中R为地球半径. 继而,可以计算出该条路径对应的仰角
(3)
由于电离层的不均匀性,射线在C1点处能经电离层反射/散射被接收站接收,如图 1所示. 此时的射线路径由于反射点角平分线不再是垂直方向的,所以电离层不均匀体的水平运动和垂直运动都会使该射线路径对应的来波信号产生多普勒频移.
根据图 1,可以得到
Δθ1=Δx1/(R+h);
(4)
θ11=D/(2R)+Δθ1;θ12=D/(2R)-Δθ1.
(5)
再根据三角形余弦定理,可分别计算出P11、P12、β11和β12,继而可以得到射线路径AC1B的群距离长度P1,根据文献[8]中双基地雷达目标多普勒频移的计算公式可以得到来波信号的多普勒频移fd1:
P1=P11+P12;
(6)
(7)
式中:α1H为水平运动速度到反射点的入出射线夹角角平分线的角度;α1V为垂直运动速度到反射点的入出射线夹角角平分线的角度.
假设射线在某Ck点处也能经电离层反射被接收站接收,则有:
Δθk=Δxk/(R+h);
(8)
(9)
计算出Pk1、Pk2、βk1和βk2,继而可以得到射线路径ACkB的群距离长度Pk以及来波信号的多普勒频移fdk.
同样,由于电离层的不均匀性,仰角逐渐增加的射线也能经电离层反射被接收站接收,可用上述相同方法计算射线路径的群距离长度和来波信号的多普勒频移.
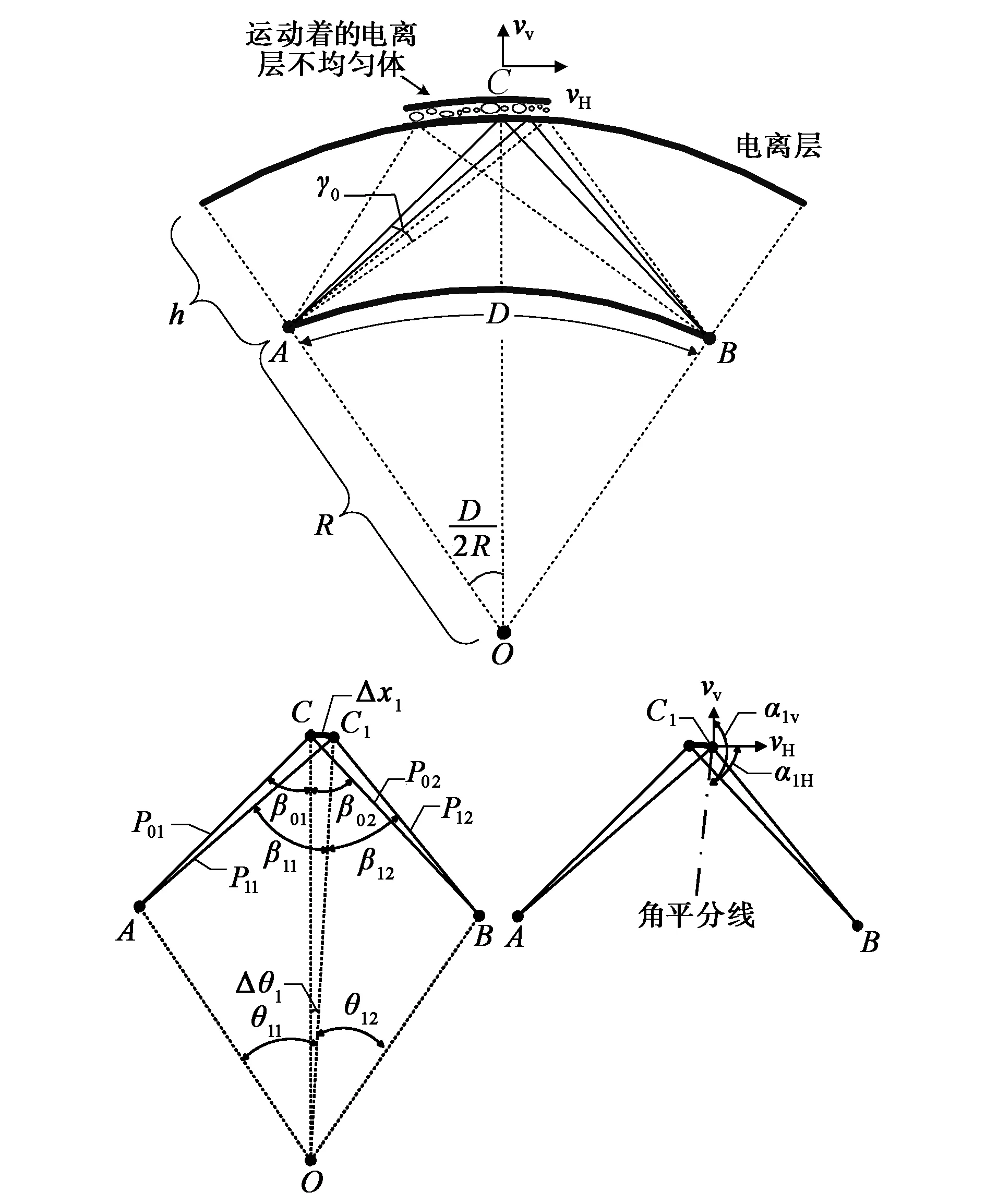
图1 运动着的电离层不均匀体反射/散射简单模型(注:下面两幅图是为了方便标出某些变量而画的简图)
2 结果分析
2.1 理论仿真分析
仿真时,假设探测频率为4.378 MHz,收发站地面距离为771 km,考虑E层传播模式,经中点反射的射线传播群距离为819 km,接收站能够接收到经对称于反射中点左右各300 km范围内不均匀体反射/散射的信号,则射线仰角范围为7.4°~53.6°.
图2~4分别给出了电离层不均匀体以不同速度运动时,根据理论模型计算得到的群距离-多普勒谱图.
图2给出了电离层不均匀体只存在水平速度分量(向右)时的情况. 由图 2可以看出:随着射线路径对应的散射点距反射中点距离的增大,射线的群距离逐渐增大,来波信号的多普勒频移也逐渐增大,并且水平速度越大,多普勒频移随群距离增大而增大得越快. 此时电离层不均匀体向右运动,则经中点处以右的不均匀体散射的信号会产生负的多普勒频移,以左的不均匀体散射的信号会产生正的多普勒频移.
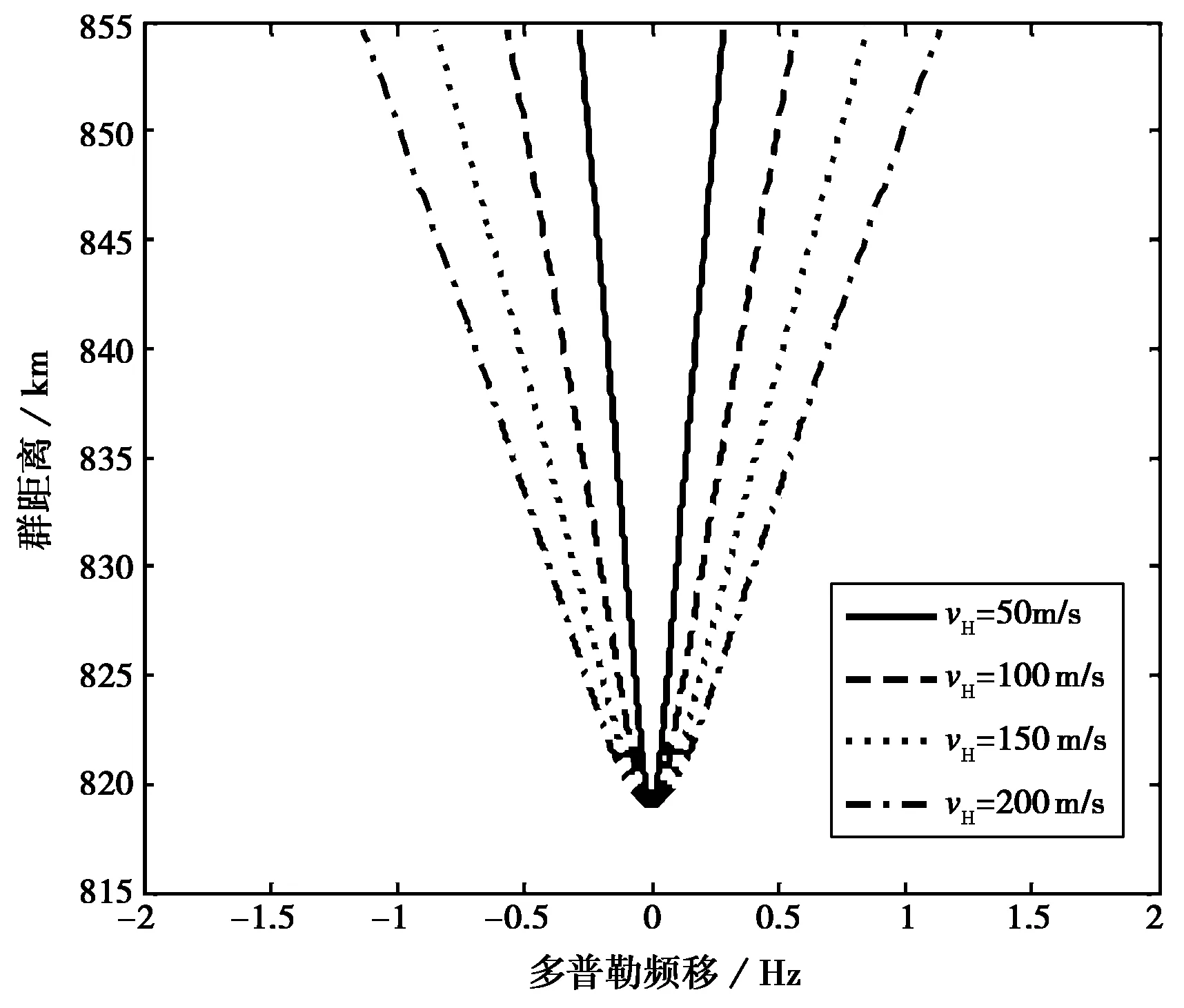
图2 不同水平速度分量计算得到的“微笑图”
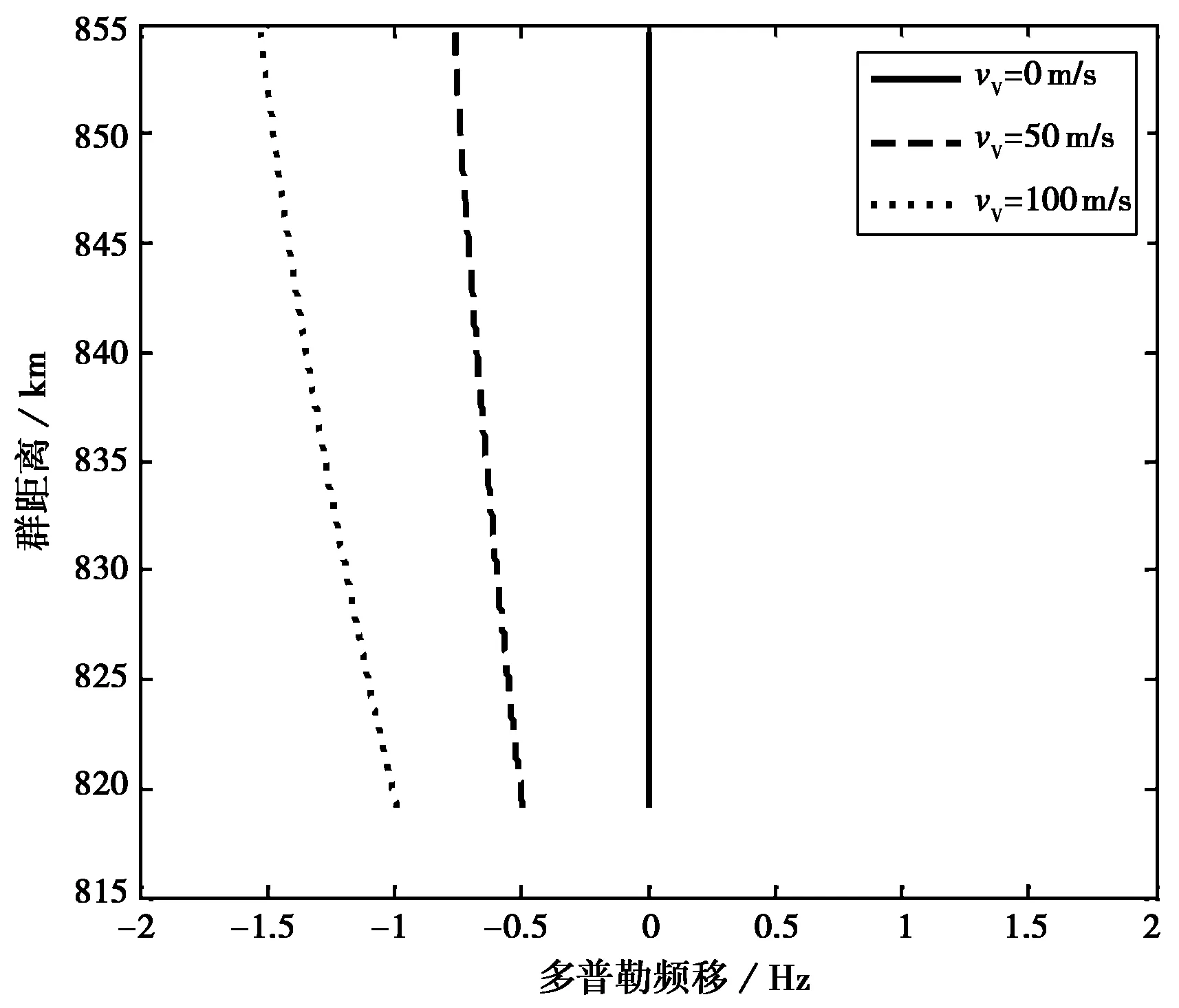
图3 不同垂直速度分量计算得到的“微笑图”
图3给出了电离层不均匀体只存在垂直速度分量(向上)时的情况. 由图 3可以看出:当不均匀体不做水平运动时,得到的群距离-多普勒谱图只是有距离扩展的谱线,当不均匀体垂直向上运动时,谱图会整体产生负多普勒频移,当不均匀体垂直向下运动时,谱图会整体产生正多普勒频移,随着群距离的增大,多普勒频移越大,并且垂直速度越大,整体频移越大. 电离层不均匀体的垂直运动,对经中点处以右的不均匀体散射的信号和以左的不均匀体散射的信号产生的影响一样.
图4给出了电离层不均匀体同时存在水平速度分量(向右)和垂直速度分量(向上)时的情况. 由图 4可以看出:由于此时两种速度分量同时作用,经中点处以右的不均匀体散射的信号和以左的不均匀体散射的信号多普勒频移随群距离的变化趋势不再对称.
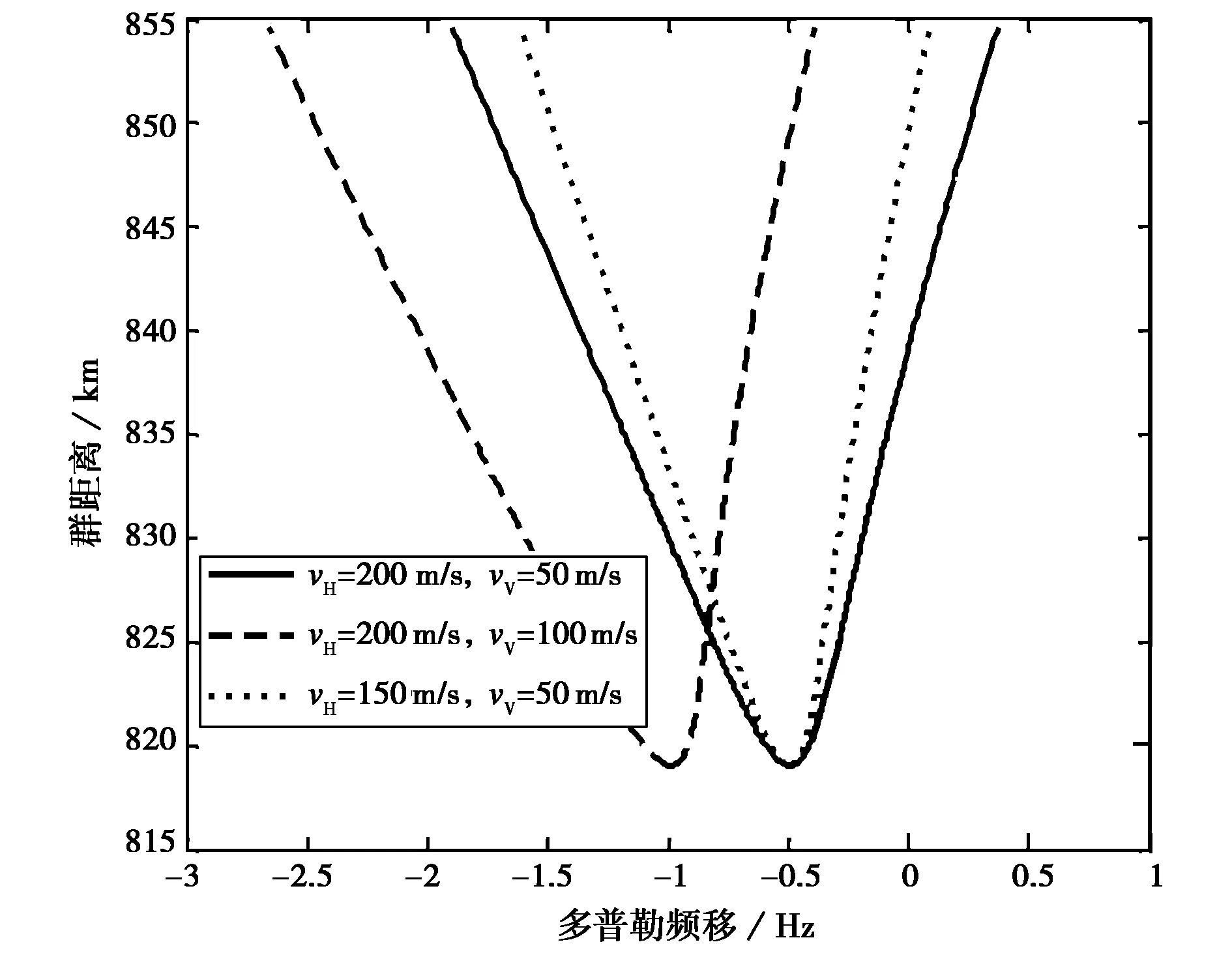
图4 不同水平和垂直速度分量计算得到的“微笑图”
前面仿真时,假设不均匀体区域对称于反射中点,下面考虑不对称的情况. 假设接收站能够接收到经反射中点以左300 km和以右200 km范围内不均匀体反射/散射的信号,则和图 4相同仿真条件下得到的结果如图 5所示.
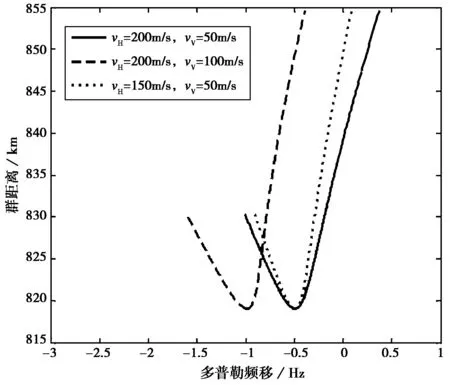
图5 考虑不均匀体区域时不同水平和垂直速度分量计算得到的“微笑图”
2.2 实测结果分析
以下是2009年12月4日20∶10∶00分录取的斜测试验数据. 探测信号为相位编码信号(P4码),相位编码个数为400,子码调制时间为50 μs,工作频率为4.378 MHz. 根据斜测扫频电离图(如图 6所示),此时,存在着四种传播模式:Es层、F2层低角及高角O、X模式.
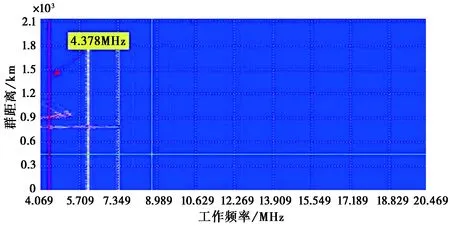
图6 斜测扫频电离图
图7~9给出了不同时间(分别为:20∶10∶16、20∶23∶47和20∶37∶18)实测的群距离-多普勒谱图,相干积累时间为32 s,多普勒分辨率为0.031 3 Hz. 结合扫频图可知:起始群距离出现在约819 km的信号为Es层信号,起始群距离约为900 km的是F2层信号,低角及高角O波、X波无明显界限,但最小群距离处对应的是F2层低角信号.
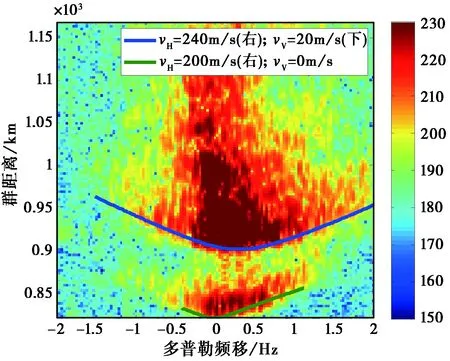
图7 群距离-多普勒谱图(20∶10∶16)
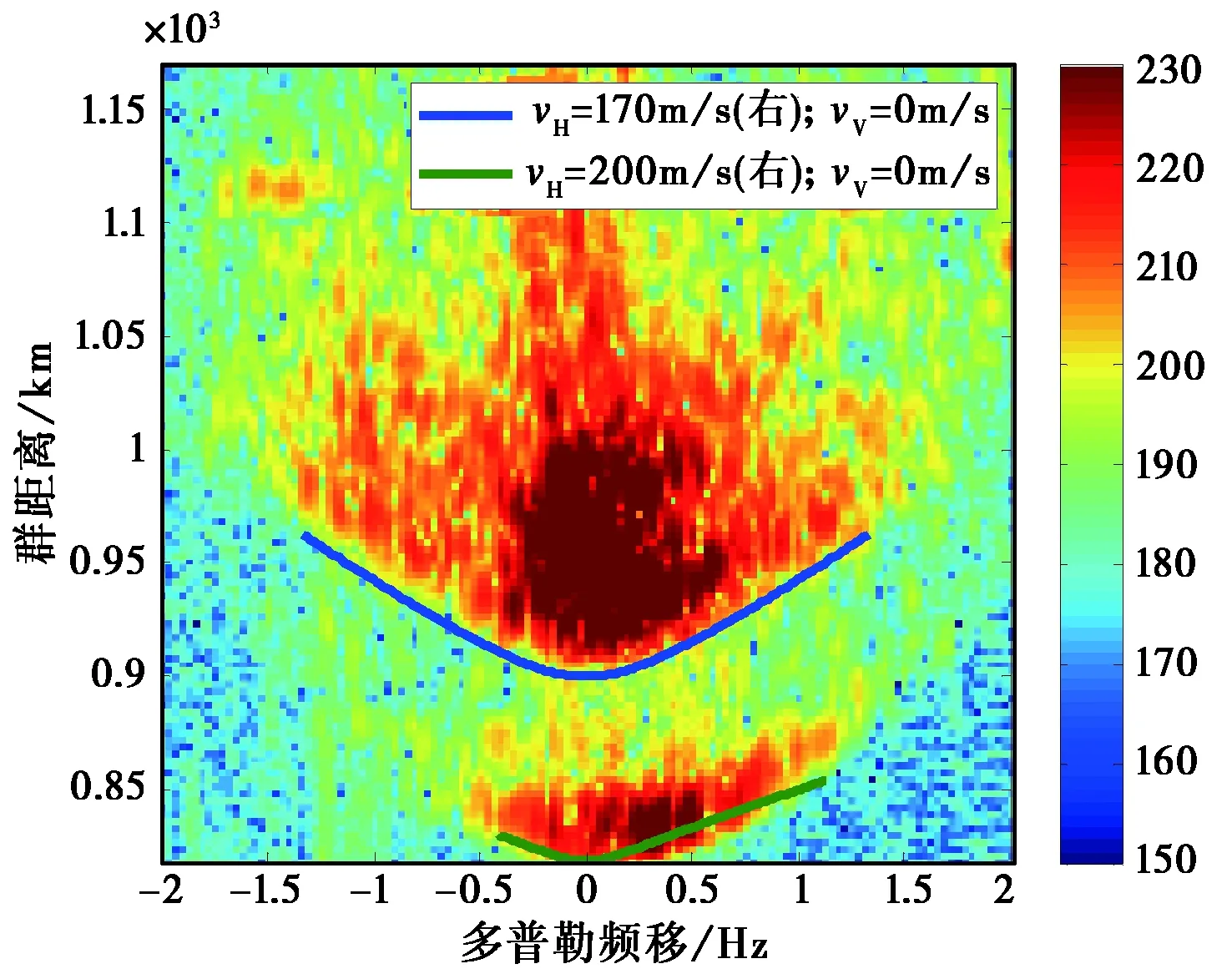
图8 群距离-多普勒谱图(20∶23∶47)
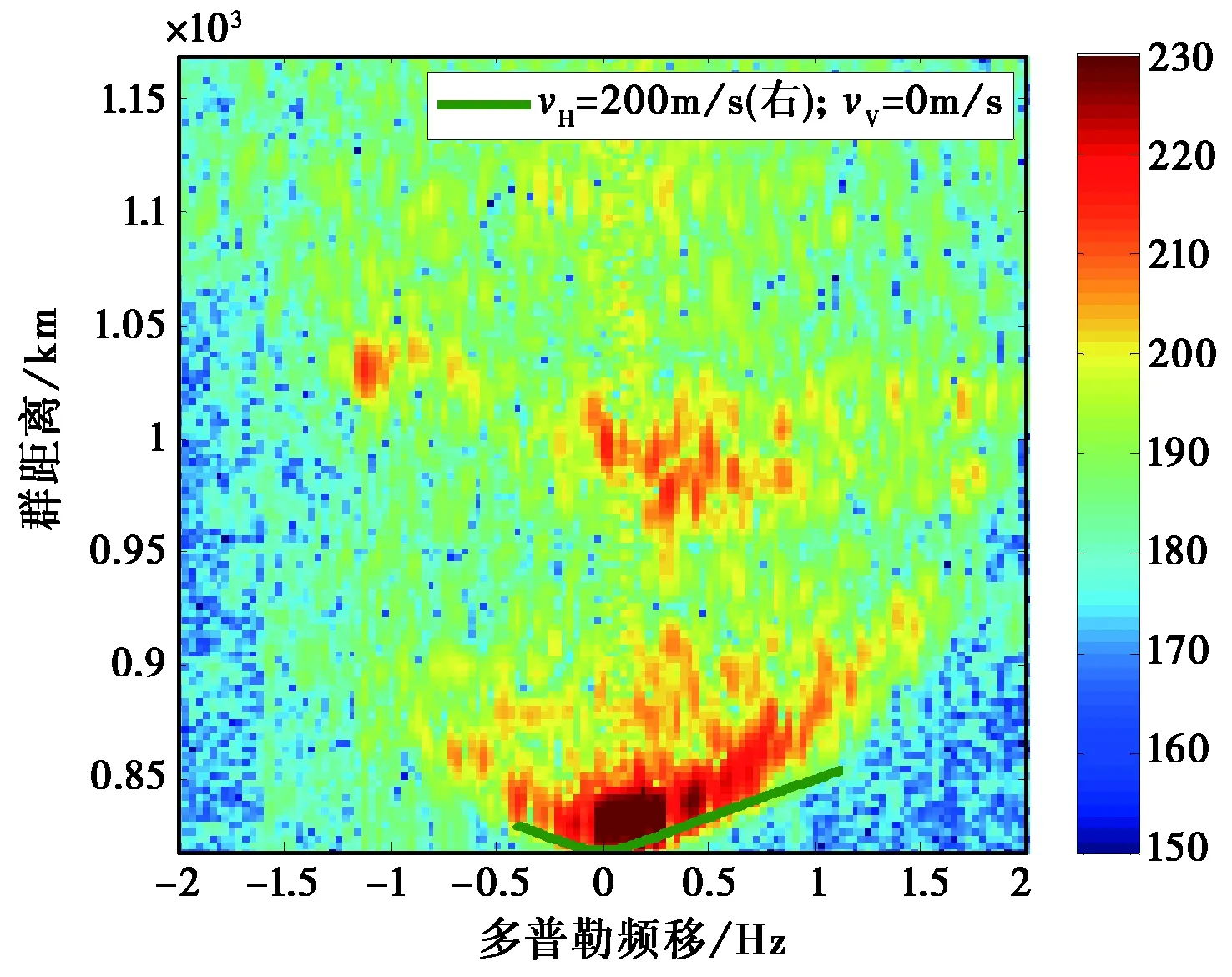
图9 群距离-多普勒谱图(20∶37∶18)
由图7~9可以看出,无论Es层信号还是F2层信号都呈现出明显的“微笑”特征,根据前面的分析,造成此种现象的原因是反射区是运动着的电离层不均匀体,因此采用2.1的分析方法,对群距离-多普勒谱图进行仿真,估计电离层不均匀体的运动速度.
图7~9中绿色粗线是对Es层信号群距离-多普勒谱图的仿真,图 7~8中蓝色粗线是对F2层低角信号群距离-多普勒谱图的仿真. 仿真时,假设F2层不均匀体在反射中点以左300 km和以右300 km范围内,Es层在反射中点以左300 km和以右200 km范围内,可以看出,仿真的群距离-多普勒谱图和实测群距离-多普勒谱图的“前沿”吻合得非常好. 在持续的27 min连续观测中,Es层的运动速度基本不变,为水平向右200 m/s,F2层低角信号不均匀体的运动速度呈现逐渐降低的趋势,从一开始的水平向右240 m/s、垂直向下20 m/s降低到水平向右170 m/s、垂直向下0 m/s,然后水平速度继续降低,直到来波信号变得很弱,如图 10所示. 另外,实测的群距离-多普勒谱图和仿真的相比存在一定的厚度,且复杂得多,这主要是因为仿真时考虑不均匀体为一薄层,而实际上不均匀体是有一定厚度的,且在不同的高度上,可能有着不同的运动速度.
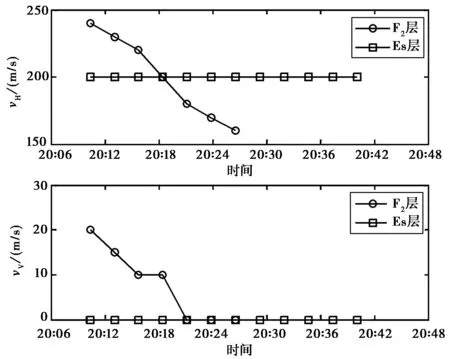
图10 不均匀体运动速度随时间的变化
由图 7~9还可以看出F2层低角信号群距离-多普勒谱图基本对称,而Es层信号群距离-多普勒谱图明显不对称,根据仿真结果可知,这主要是由于反射/散射信号的Es层区域没有对称于反射中点. 需要说明的是,在和实测值进行关联时,并不能根据仿真的群距离-多普勒谱图给出电离层不均匀体的实际大小,因为接收站收到的是经某一范围内不均匀体反射/散射的信号. 但是,由图 8至少可以说明F2层不均匀体尺度大于600 km,Es层尺度大于500 km.
3 结 论
针对斜向探测试验得到的定频群距离-多普勒谱图上出现的“微笑”特征,指出电波经由运动着的电离层不均匀体反射/散射到达接收站是产生多普勒维和群距离维均扩展的“微笑”谱图的原因,通过建立理论模型,仿真得到了运动着的电离层不均匀体情况下的群距离-多普勒谱图,与实测谱图“前沿”吻合得很好,并根据模型参数估计出了不均匀体的运动速度.
文中理论模型的构建基于简单的几何形状和理想的电离层不均匀体运动状态,实际中,电离层并不是简单的球形,不均匀体也具有一定的厚度,且不同高度处运动速度也不相同等等. 如果所有这些因素都考虑,可能会得到和实测谱图更加一致的结果,但势必会增加模型的复杂程度,这是今后需要努力研究的工作.
参考文献
[1] 焦培南, 张忠治. 雷达环境与电波传播特性[M]. 北京: 电子工业出版社, 2007: 278-279.
[2] KOKOUROV V D, KAZIMIROVSKY E S, et al. The simultaneous measurements of ionospheric drifts by vertical and oblique sounding[J]. Journal of Atmospheric and Terrestrial Physics, 1971, 33(6): 943-950.
[3] 张秀菊, 焦培南, 姜炳武, 等. 利用高频返回散射技术探测电离层大尺度扰动[J]. 空间科学学报, 1988, 8(2): 138-144.
ZHANG Xiuju, JIAO Peinan, JIANG Binwu, et al. LSTID measured by the technique of the HF backscattering sounder[J]. Chinese Journal of Space Science, 1988, 8(2): 138-144. (in Chinese)
[4] 焦培南, 凡俊梅, 吴海鹏, 等. 高频天波返回散射回波谱实验研究[J]. 电波科学学报, 2004, 19(6): 643-648.
JIAO Peinan, FAN Junmei, WU Haipeng, et al. The experimental research of the Doppler spectrum by HF skywave backscattering[J]. Chinese Journal of Radio Science, 2004, 19(6): 643-648. (in Chinese)
[5] 凡俊梅, 马小村, 李 雪, 等. 电离层不均匀体对短波信号影响的实验研究[J]. 电波科学学报, 2008, 23(3): 443-448.
FAN Junmei, MA Xiaocun, LI Xue, et al. Experiment research on effect of ionospheric irregularities on HF signal[J]. Chinese Journal of Radio Science, 2008, 23(3): 443-448. (in Chinese)
[6] 凡俊梅, 焦培南, 吴振森, 等. 电离层不同传播模式信号多普勒频移的实验研究[J]. 电波科学学报, 2008, 23(1): 34-40.
FAN Junmei, JIAO Peinan, WU Zhensen, et al. Experiment research on ionospheric Doppler shift for different propagation[J]. Chinese Journal of Radio Science, 2008, 23(1): 34-40. (in Chinese)
[7] LYNN K J W. Ionospheric observations made by a time-interleaved Doppler ionosonde[J]. Advances in Space Research, 2008, 42(7): 1218-1230.
[8] WANG Jian, DIZAJI R, et al. Analysis of clutter distribution in bistatic high frequency surface wave radar[C]// Proceedings of the IEEE Canadian Conference on Electrical and Computer Engineering, May 2-5, 2004(3): 1301-1304.
