基于ANSYS的舰船武器装备基准变化分析方法*

张 磊，王安国，李 辉

(海军大连舰艇学院，辽宁 大连 116018)

尽管舰船强度和刚度很高，但在载荷、海浪压力等外部环境的作用下，船体会产生变形［1-2］，舰船甲板面装有的各种武器装备和设备的安装基准面会随船体的变形而发生变化，这种基准的变化影响武器系统的打击精度。本文提出了一种基于ANSYS的舰船武器装备基准变化分析方法，对武器装备基准变化及其影响进行分析，研究舰船航行状态下武器装备基准的变化情况。

1 武器装备基准变化及其影响

以舰炮武器系统为例说明武器装备基准的重要作用，如图1所示，该舰炮武器系统的工作原理:由搜索雷达A通过本舰作战指挥系统给舰炮跟踪雷达B作出目标指示，跟踪雷达将跟踪并测得的目标参数送至火控台，火控台根据目标参数、弹道特性和平台罗径C给出的本舰参数，解算出射击诸元，舰炮D到指令位置实施火力攻击［3］。

图1 典型武器系统布置图

舰船在海上航行，受到了自身载荷变化、武器发射、风浪等因素的综合作用，作为弹性物体，舰船必然发生弹性变形，因而图1中A、B、C、D处的首尾线方向和纵横摇姿态角各不同。舰载武器系统往往由多个设备组成，布置在舰船不同层甲板、不同部位，以往舰载武器系统射击、导引诸元解算中，往往将船体视作刚体，只考虑了舰船在海上的刚体运动，而没有考虑不同位置间的相对位移，这种简化处理将影响武器系统作战效能的正常发挥，甚至造成武器系统完全失效。随着舰炮武器系统、舰载导弹武器系统精确打击性和综合打击能力的提高，武器对舰载航向姿态基准信息的准确性、稳定性等战术技术要求不断提高。同时，随着舰船排水量、主尺度的不断加大，舰船波浪中航行时弹性变形也有增大的趋势，武器精确打击和舰艇弹性变形之间的矛盾日益突出。

目前一般由在武器装备处设置捷联垂直参考基准为火控系统解相遇问题提供所需要的航向角、纵摇角和横摇角等信息，但检测精度会随时间累积而退化，并且受安装数量的限制，不能得到所有装备基准面变化情况［4-5］。目前在船体结构分析中有限元法已占主导地位，为了解决武器装备基准随外界因素变化问题，本文给出了一种基于ANSYS的舰船武器装备基准变化分析方法，研究武器装备基准受外部环境影响的变化规律。

2 舰船有限元模型的建立

2.1 有限元计算工具简介

有限元法的基本思想是将物体离散成有限个且按一定方式相互联结在一起的单元组合，来模拟或逼近原来的物体，物体被离散后，通过对其中各个单元进行分析，最终得到对整个物体的分析。有限元法的出现使传统的船舶结构力学方法及结构强度计算方法发生了根本变革，过去手工计算方法不能解决的问题，用有限元法迎刃而解。本文选用ANSYS作为有限元分析的工具［6］。ANSYS软件是目前著名的通用工程有限元软件之一，它是融结构、热、流体、电磁、声学于一体的大型有限元分析软件。由美国ANSYS/Mechanical U公司开发，能与多数CAD软件接口，实现数据的共享和交换，如 Pro/Engineer、NASTRAN、Alogor、I-DEAS、Auto-CAD等。

2.2 有限元建模原则

船体的甲板、底板、纵舱壁、横舱壁、肋板等构件为平面板，采用一次壳单元SHELL63;船体外板为曲面板，经离散为平面单元后也采用一次壳单元SHELL63模拟;各类板构件的扶强材，如甲板纵骨、舷侧肋骨、甲板横梁、舱壁扶强材等采用线性梁单元 BEAM188建模。

本文分析的重点是船体甲板面随外界载荷变化的变形情况，进而探究舰艇武器基准的变化规律。因而需要详细地建立所有主要结构构件的有限元模型，板材的厚度分布，型材的分布以及加强形式等都要符合实际情况。

图2为某型舰船主体结构模型。选取的某型舰船主要船型结构参数为:总长120.8m，垂线间长110.0m，型宽12m，型深9.8m，设计吃水5.6m，结构吃水7.6m，模型的节点总数为17837，单元总数为17724，其中SHELL63为2796，BEAM188为17928。

2.3 网格划分

网格的质量对有限元分析结果的精确性有重要的影响。网格划分的不好，会导致局部应力过大或者过小，从而无法正确判断应力大的部位是否由于结构薄弱引起的，进而可能导致整个分析结论不可靠。

图2 船体结构有限元模型

由于三角形单元难于变形，因而计算的精确性远不比四边形单元。本文在网格划分过程中，板单元主要划分为四边形单元，仅在边界处存在少量的三角形单元。

网格的质量(如单元的细长比、网格内角、锥度比、翘曲量以及拉伸值等参数)会直接影响到有限元计算结果的精确性。因而在网格划分前，判断欲实施的网格划分方案是否有可能产生低质量的网格。如果可能产生坏单元，需要调整网格划分方案避免其发生。根据驳船结构模型的特点，实际中定义符合以下任何一条的单元为坏单元:细长比大于10;网格内角小于15度;锥比度小于0.1;拉伸值小于0.1。

网格划分时要保证相交板材、型材在交线处具有公用节点，因而网格纵向按照肋位划分，垂向与横向按照甲板、横向扶强材、垂向扶强材等构件所在理论线划分网格。

3 舰船力载荷的计算

影响船体总体强度的外部载荷主要由装载、静水浮力和波浪诱导载荷三项组成。前两项比较明确，可以由设计的构件尺寸、船舶的吃水和型线计算得到。而后者是由于波浪引起的船体载荷，可以利用三维载荷计算方法，计算出舰船在波浪中所受的水动压力和惯性力。

3.1 重力浮力载荷

通常将船体沿船长方向平均分成20个理论站，将船舶载荷按理论站分布，保持每一项载荷的分布范围和作用点基本不变，且认为每一理论站内的载荷是均匀分布的，用阶梯形载荷分布代替真实的载荷分布。这种方法求得的载荷分布虽然与实际情况有所差别，但不会对计算带来明显误差。本文取舰船装载为空载状态，重量分布以均布载荷的形式直接施加到船体模型的相应位置，根据邦戎曲线即可求得船舶在空载状态下的静水浮力曲线，从而得到船舶静水浮力分布 。

3.2 波浪诱导载荷

波浪引起的船体载荷是随机统计量，需要根据现有的海洋与河流波浪统计资料将船体置于真实的海浪环境中，计算船体在波浪上的运动和载荷。用三维波浪载荷计算方法计算整体舰船在规则波中的运动、剖面载荷以及横剖面脉动压力的频率响应函数，利用三维计算方法所得的相位角以及波幅，计算出惯性加速度。将所得到的波浪压力以及惯性加速度施加到舰船模型上［8］。

依据船舶实际航行海区建立海浪统计资料，作为船舶结构设计计算时确定载荷的依据，我国及全球各大海域频繁出现的海情为3级～5级浪(Hs≈0.5m～4.0m)，6级浪(Hs≈4.0m～6.0m)出现频率较低。为了得到武器装备基准的最大变化量，选取h=6m为极限波高，波长等于船长的坦谷波作为船舶遭遇的极限波浪，计算空载状态时舰船顶浪和斜浪两种状态下的船体甲板面形变量。

3.3 边界条件

船舶处于航行状态时，海水对船体的支撑显示出很强的弹性，因而将船体外板上处于水线以下的节点当作垂向弹性支撑处理，用ANSYS的combin14单元模拟，其约束刚度可以表示为

其中，k为水弹性约束刚度;ρ为海水密度;g为重力加速度;B和L分别为水线船宽和船长。为精确计算结果，以理论站为单位确定约束刚度，此时L表示站长，B为理论站平均水线船宽。

为防止船体产生刚性位移，在首尾防撞舱壁水线处选取一组节点，施加纵向和横向约束［7］。

4 力载荷作用下的基准变化分析

按照上述力载荷计算方法对船体有限元模型施加载荷，计算舰船空载状态，受顶浪和斜浪作用时，船体有限元模型甲板面的位移量，进而可以分析甲板面武器装备基准变化的一般规律。

海况一:船体受顶浪作用，波浪波长为120m，波高6m，船体只存在纵摇无横摇，当舰首向上纵摇达到最大时，甲板面的变形量如图3所示。

当舰首向下纵摇达到最大时，甲板面的变形量如图4所示。

从模拟结果来看，舰尾的变形量最大，两种情况下分别达到7.714mm和8.712mm;纵摇舰首向上时，舰首变形量最小，舰首向下时，变形量最小部位于船中。由于主机位于船尾，空载状态机舱部位重量较大，所以尾部对纵摇的惯性力较敏感，由此可知模拟的结果与真实情况一致。

图3 海况一舰首向上甲板面变形量

图4 海况一舰首向下甲板面变形量

海况二:船体受30°斜浪作用，海浪波长为120m，波高6m，船体既有横摇又有纵摇，当舰首向上横摇和纵摇均达到最大时，甲板面的变形量如图5所示。

当舰首向下横摇和纵摇均达到最大时，甲板面的变形量如图6所示。

从模拟结果来看，当舰船既有横摇又有纵摇所引起的变形量远大于只有纵摇引起的变形量，并且越靠近两舷变形量越大，两种海况的最大变形量都发生在舰尾两舷，分别达到39.511mm和39.274mm，船中部位变形量最小也达到了27.19mm。

由以上模拟和分析可以看出，就此类型船体而言，横摇对于甲板变形起决定性作用，纵摇引起的船体变形有限，这也与该船上甲板与首楼甲板之间的连接形式有关，即舷墙有大量开口，使船体结构对于横向惯性力比较敏感，并且船尾部有较大的舱室，致使尾部扭曲变形较大。分布于甲板面的武器装备基准变化主要是由船体变形所引起的，所以针对此类型舰船，横摇使装备基准影响产生较大变化，并且靠近尾部和两舷的装备基准变化较明显。所以当舰船在风浪条件下航行需要使用武器装备时，应控制舰船为顶浪航向，避免舰船出现横摇的现象，这样更有利于武器装备作战效能的发挥。

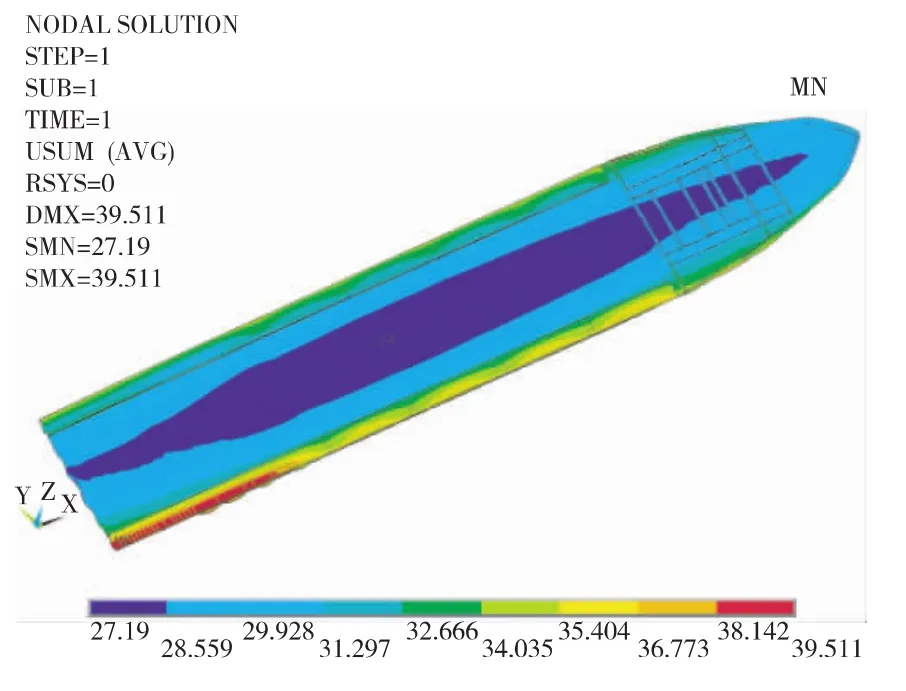
图5 海况二舰首向上甲板面变形量

图6 海况二舰首向下甲板面变形量

5 结束语

本文应用ANSYS建立某型舰船的有限元模型，利用三维波浪载荷计算方法模拟极限海况下的波浪力，得到舰船甲板面武器装备基准在两种极限海况下的变化规律，并给出了指导武器装备作战使用的建议。所得结论只在本文所选取的某型舰船主体结构条件下成立，但应用此方法可以研究不同类型舰船，在航行状态下武器装备基准的变化情况，从而为武器系统作战效能的发挥提供参考。

［1］万德钧，刘玉峰.消减舰船变形的影响和为全舰提供高精度姿态基准［J］.中国惯性技术学报，2005，13(4):77-82.

［2］朱昀炤，汪顺亭，缪玲娟.船体变形测量技术综述［J］.船舶工程，2007，29(6):58-61.

［3］刘芳华.舰船变形状态监测与预报的关键技术研究［D］.镇江:江苏科技大学，2011.

［4］郑梓祯，刘德耀，蔡迎波.船用惯性导航系统海上试验［M］.北京:国防工业出版社，2006.

［5］郑梓祯，刘德耀，蔡迎波.船用惯性系统试验安装标校与变形测量［J］.中国惯性技术学报，2004，12(4):1-6.

［6］钟骏平，程远胜，刘均，等.基于ANSYS的船舶纵向下水弹性计算方法［J］.船舶力学，2007，11(5):752-758.

［7］石磊，薛冬新，宋希庚.用于轴系校中的船体变形计算研究［J］.船舶工程，2010，32(3):13-16.

［8］魏弘.舰船结构在波浪中的整体弹性变形分析［D］.哈尔滨:哈尔滨工业大学，2003.